контрольная гидравлика. КОНТРОЛЬНАЯ 2. Отчет о выполнении контрольной работы по Гидравлика и нефтегазовая гидромеханика
 Скачать 361.31 Kb. Скачать 361.31 Kb.
|
|
Министерство образования и науки Российской федерации «Тихоокеанский государственный университет» «Кафедра инженерных систем и техносферной безопасности» Отчет о выполнении контрольной работы по «Гидравлика и нефтегазовая гидромеханика» Выполнил студент заочного обучения Направление(профиль) НД(аб)з-81 Шифр  Хабаровск 2018 Хабаровск 2018ОглавлениеЗадача 16 5 Задача 27 8 Задача 47 15 Литература 16 Задача 8 Определить полную силу давления жидкости на деталь, имеющую форму четверти круглого цилиндра радиусом R и укрепленную на болтах (рис. 7). Под каким углом горизонту на деталь направлена сила давления, если напор в жидкости Ж равен Н, длина детали вдоль образующей равна b? 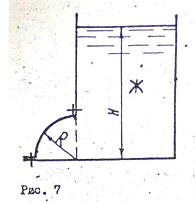 Дано: Ж – глицерин, R = 1,0 м, Н = 4,0 м, b = 3 м Р, α = ? Решение. Сила давления жидкости на криволинейные поверхности равна сумме составляющих ее сил: горизонтальной и вертикальной. 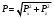 . .Определим силы давления жидкости (горизонтальную и вертикальную) на крышку. Горизонтальная составляющая силы давления жидкости на криволинейную стенку равна силе давления жидкости на ее вертикальную проекцию: 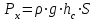 , ,где 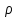 – плотность жидкости, ρ = 1245 кг/м3 [2] – плотность жидкости, ρ = 1245 кг/м3 [2]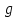 – ускорение свободного падения, – ускорение свободного падения,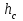 – расстояние центра тяжести от свободной поверхности жидкости, – расстояние центра тяжести от свободной поверхности жидкости,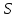 – площадь вертикальной проекции смоченной жидкостью криволинейной стенки. – площадь вертикальной проекции смоченной жидкостью криволинейной стенки.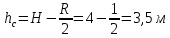 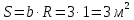 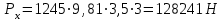 Вертикальная составляющая силы давления жидкости на криволинейную стенку равна силе тяжести жидкости в объеме 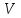 , называемом телом давления. В нашем случае тело давления представляет собой объем четверти цилиндра: , называемом телом давления. В нашем случае тело давления представляет собой объем четверти цилиндра: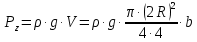 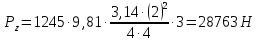 Сила давления жидкости: 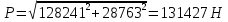 Направление силы Р определяется отношением: 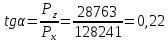 α = 130 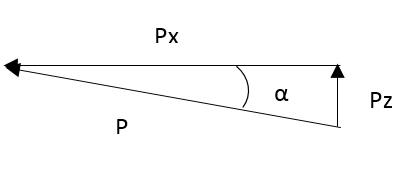 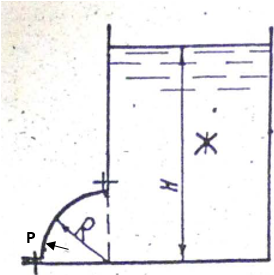 Ответ: Р = 131427 Н, α = 130 Задача 16Какое давление р0 необходимо поддерживать в резервуаре А (Н1 = 2 м), чтобы через кран (рис. 15), расположенный на пятом этаже здания (Н = 20 м), и имеющий коэффициент сопротивления ζ = 3, проходил расход воды Q? На участке трубопровода длиной l1 труба имеет диаметр d1, на участке l2 труба имеет диаметр d2. Температура воды 20 ºС, абсолютная шероховатость стенок трубопровода kэ = 0, 2 мм.   2        1 1 2 0 0 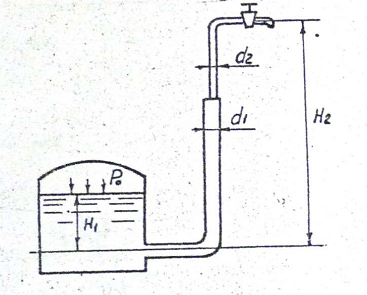 Рис. 15 Дано: Q = 7 м3/ч = 0,0019 м3/с, l1= 20 м, l2=12 м, Н1= 2 м, Н2 = 20 м, d1 = 50 мм = 0,05 м, d2 = 20 мм = 0,02 м, kэ = 0,2 мм, ζ =3 р0 = ? Решение: Составим уравнение Д. Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0, совпадающей с осью трубопровода (рис. 15). Уравнение в общем виде: 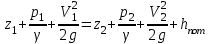 В нашем случае z1 = Н1, z2 = Н2, р1= р0 , р2=0, скоростным напором в сечении 1-1 пренебрегаем, т.к. его значение близко к 0 (скорость на поверхности жидкости в резервуаре очень мала); hпот - потери напора. Потери по длине трубопровода на каждом участке определим по формуле Дарси – Вейсбаха: 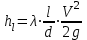 , ,где λ– коэффициент гидравлического сопротивления. Потери в местном сопротивлении определим по формуле Вейсбаха: 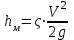 , ,где ζ– коэффициент местного сопротивления. Принимаем R/d =2 и тогда для поворотов по справочной литературе [4], ζ1= 0,15 , ζ2= 0,15, ζвс- коэффициент внезапного сужения трубопровода, ζвс≈ 0,46 Общие потери напора будут: hпот= hl+ hм 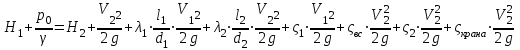 Определим коэффициент гидравлического сопротивления по графику Мурина, для этого найдем отношение: 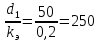 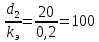 Определим числа Рейнольдса в каждом трубопроводе по формуле: 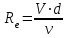 ν – коэффициент кинематической вязкости воды при данной температуре, ν = 1,01∙10-6 м2/с [2]. Скорость жидкости: 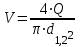 , ,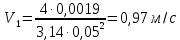 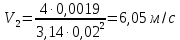 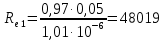 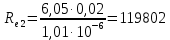 По графику Мурина [3] определяем коэффициенты гидравлического трения: λ1= 0,028, λ2= 0,038 Подставляем все найденные значения в уравнение Бернулли: 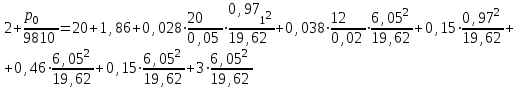 р0 = 683,5 кПа Ответ: р0 = 683,5 кПа Задача 27Вода из бака по трубопроводу длиной l3 и диаметром d3 поступает в разветвленный трубопровод, одна из ветвей которого изменяет диаметр d1 и длину l1, соответственно d2 , l2. Определить расход воды, поступающий в точки 1 и 2 , если напор равен Н (рис. 23) 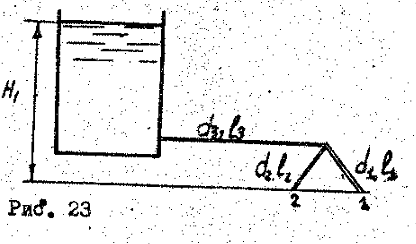 Дано: l1 = 17 м, l2 = 10 м, l3 = 11 м, d1 = 32 мм = 0,032 м, d2 = 25 мм = 0,025 м, d3 = 40 мм = 0,040 м, Н = 3,1 м Q1,2 = ? Решение. В рассматриваемом случае потери напора равны разности отметок входного и выходного сечений, Нпот = Н. На участке длиной l: Н1 = А · Q2, на участке l1: Н2 = А1 · Q2, на участке l2: Н3 = А2 · Q2, где А, А1, А2 – сопротивления трубопроводов. Общее сопротивление трубопроводов при последовательном соединении [3]: 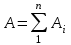 Потери напора при последовательно-параллельном соединении трубопроводов вычисляем по уравнению: 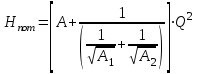 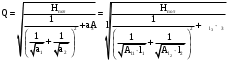 Сопротивления отдельных трубопроводов (А) определяют по формулам или по справочнику. Примем в первом приближении значения: Аl1 = 93860 с2 /м6, Аl2 = 436700 с2 /м6 , Аl3 = 44530 с2 /м6 [3], затем их уточним. 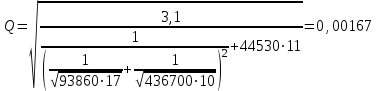 м3/с м3/сУдельное сопротивление можно определить по формуле: 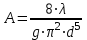 . .Определим скорости движения жидкости в трубопроводах: 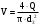 , , 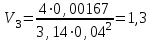 м/с м/сОпределим расходы в параллельных ветвях трубопровода: Q = Q1 + Q2, т.к. соединение параллельное. Предположим, что расходы в параллельных ветвях приблизительно равны и составляют Q/2 = 0,000835 м3/с. 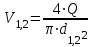 , , 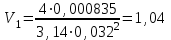 м/с м/с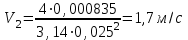 Для определения коэффициента гидравлического трения выясним, какой режим движения жидкости в трубопроводах. 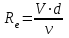 , ,где ν = 1,01·10-6 м2/с – кинематическая вязкость, принятая по справочной литературе [2] 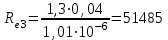 , режим турбулентный. , режим турбулентный. Коэффициент сопротивления λ определяем по формуле Альтшуля: 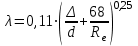 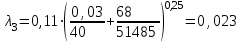 где Δ = 0,03 мм – абсолютная шероховатость материала труб (принимаем для стали по справочной литературе [2]). 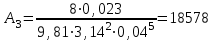 с2/м6 с2/м6Аналогично определяем А для других трубопроводов. 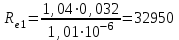 - режим турбулентный. - режим турбулентный.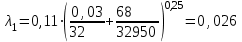 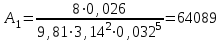 с2/м6 с2/м6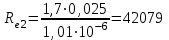 - режим турбулентный. - режим турбулентный.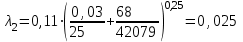 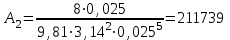 с2/м6 с2/м6Уточним расход жидкости: 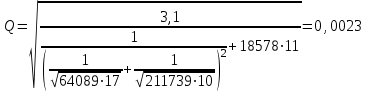 м3/с м3/сQ = Q1 + Q2 = 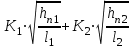 , ,где К1 и К2 - коэффициенты расхода 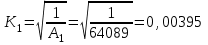 м3/с м3/с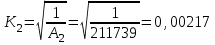 м3/с м3/сОпределим потери напора hl - потери напора на участке длиной l3 hl = 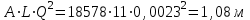 Потери напора в параллельных ветвях: hп1 = hп2 = 3,1 – 1,08 = 2,02 м Q1 = 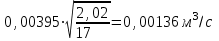 Q2 = 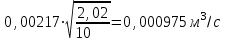 Ответ: Q1 = 0,00136 м3/с, Q2 = 0,000975 м3/с Задача 40 Вода при температуре t° С протекает в количестве Q в горизонтальной трубе кольцевого сечения, состоящей из двух концентрических оцинкованных стальных труб. Внутренняя труба имеет наружный диаметр Д1, а наружная труба имеет внутренний диаметр Д2. Найти потери напора по длине L. Дано: Q = 0,02 м3/с, Д1 = 10 см = 0,1 м, Д2 = 12 см = 0,12 м, t = 18 0С, L = 10 м hl= ? Решение. Потери напора по длине определяем по формуле Дарси: 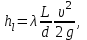 где λ – коэффициент гидравлического трения, зависящий от режима движения жидкости; υ – средняя скорость движения жидкости. Для определения режима движения воды необходимо рассчитать значение критерия Рейнольдса. Re= 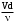 , ,где ν - кинематическая вязкость жидкости, м2/с; при данной температуре – 1,06·10-6 м2/с [2]. Поскольку вода протекает в кольцевом пространстве между наружной и внутренней трубами, то для данного случая будем рассчитывать эквивалентный диаметр. Re= 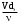 , ,Для канала кольцевого поперечного сечения, в котором жидкость ограничена внутренней и наружной окружностями с диаметрами dвн и dн = Dсоответственно, эквивалентный диаметр: 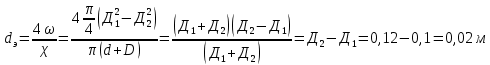 Для определения скорости движения жидкости воспользуемся формулой: 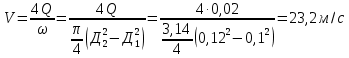 Режим движения: 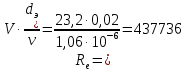 Re>2320, следовательно, характер движения воды - турбулентный Определим коэффициент трения по универсальной формуле Альтшуля: 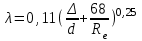 , ∆ - абсолютная шероховатость, ∆ = 0,12 мм [2]. , ∆ - абсолютная шероховатость, ∆ = 0,12 мм [2].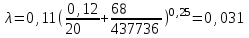 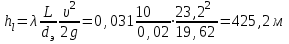 Ответ: hl = 425,2 м Задача 47Определить гидравлическую крупность шарообразной частички диаметром d с удельным весом γ, которая равномерно осаждается в жидкости (или газе), имеющей плотность ρ. Дано: d = 0,2 мм = 0,0002 м, ρ = 1,15 кг/м3, γ = 53900 Н/м3 w = ? Решение. Определим скорость осаждения частицы (гидравлическую крупность) по формуле [5]: 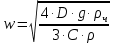 где ρч – плотность частицы, ρч = γ/g = 53900/9,81 = 5494 кг/м3 С – коэффициент сопротивления, для шарообразной частицы С = 0,45, [3] 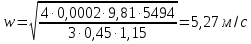 Ответ: w = 5,27 м/с Литература1. Методические указания для выполнения контрольной работы. 2. Примеры расчетов по гидравлике. Под ред. А.Д. Альтшуля. Учеб. пособие для вузов. М., Стройиздат, 1977. 255 с. 3. Я.Н. Флексер. Практикум по гидравлике и сельскохозяйственному водоснабжению. 4. Метревели В.Н. Сборник задач по курсу гидравлики с решениями: Учеб. пособие для вузов/ В.Н. Метревели.- М.: Высш. шк., 2007.- 192 с.: ил. 5.http://www.ibrae.ac.ru/docs/3(19)/040_047_Arktica_3(19)_09_2015.pdf, http://www.ccas.ru/depart/Palcev/doc/2011/Lambert_book_ISBN-978-3-8443-5430-0.pdf |
