ЗАЯВКА Караева. Отчет о выполнении практических работ по дисциплине Патентоведение

• Название: Отчет о выполнении практических работ по дисциплине Патентоведение
• Дата: 17.05.2023
• Размер: 0.49 Mb.
• Имя файла: ЗАЯВКА Караева.docx
• Тип: Отчет; #1139548
• страница: 1 из 3

Северо-Кавказский федеральный университет

Институт цифрового развития

ОТЧЕТ

о выполнении практических работ по дисциплине

«Патентоведение»

Выполнила: Караева Альбина

студент 1 курса, уч. гр. ИБАС-с-о-22-1 специальности «Информационная безопасность автоматизированных систем» очной формы обучения

Проверил зав. каф. ОТЗИ К.т.н., доцентВ.И. Петренко

G06F 7/12, H 03 В 29/00

ЦИФРОВОЙ ИМИТАТОР СЛУЧАЙНЫХ СИГНАЛОВ

 Изобретение относится к областям радиотехники и измерительной техники и может быть использовано для имитации сигналов и помех при тестировании аппаратуры радиосвязи и систем управления.

Известен цифровой генератор хаотического сигнала [1] на базе регистра сдвига и аналогового источника шума, формирующий «истинно случайный» цифровой сигнал с равновероятными отсчетами, в котором отсутствует возможность изменения статистических характеристик сигнала.

Известны цифровые генераторы [2] псевдослучайных двоичных последовательностей (например, М-последовательностей, последовательностей Гоулда, Кассами и др.), формируемых с помощью регистров сдвига с линейными или нелинейными обратными связями. Известен [3] датчик случайных чисел с равномерным распределением вероятностей, в котором используются записанные в блоке памяти случайные числа, которые «перемешиваются» с помощью двоичных счетчиков, улучшая качество совпадения формируемых чисел с теоретическим равномерным законом распределения вероятностей. Их недостатком является отсутствие возможностей формирования псевдослучайных чисел с различными законами распределения вероятностей.

Известен имитатор радиосигналов [4], содержащий генератор опорной частоты, блок памяти, устройство считывания данных, цифроаналоговый преобразователь. Устройство имитирует сигналы произвольного вида, представленные модельными файлами данных или цифровыми записями сигналов, которые предварительно записываются в блок памяти и считываются в процессе имитации. Его недостатком является ограниченность продолжительности воспроизводимой реализации, что особенно существенно при высокочастотном считывании данных.

Наиболее близким по технической сущности к предлагаемому устройству является цифровой имитатор случайных сигналов [5], содержащий генератор опорной частоты, блок памяти, цифроаналоговый преобразователь, генератор равновероятных псевдослучайных чисел и регистр.

Задачей предлагаемого технического решения является уменьшение требуемой емкости блока памяти при формировании двоичных случайных чисел.

Поставленная задача решается тем, что цифровой имитатор случайных сигналов, содержащий генератор опорной частоты, блок памяти, цифроаналоговый преобразователь, генератор равновероятных псевдослучайных чисел и регистр, дополнительно содержит цифровой компаратор, первый вход которого подключен к выходу генератора равновероятных псевдослучайных чисел, второй вход - к выходу блока памяти, регистр последовательных приближений, тактовый вход которого подключен к третьему выходу генератора опорной частоты, управляющий вход - к выходу цифрового компаратора, а выход параллельно соединен с первым адресным входом блока памяти и входом регистра, и буферный регистр, вход которого подключен к выходу регистра последовательных приближений, а выход - к входу цифроаналогового преобразователя, выход регистра соединен со вторым адресным входом блока памяти, а его тактовый вход - со вторым выходом генератора опорной частоты, тактовый вход генератора равновероятных псевдослучайных чисел подключен к первому выходу генератора опорной частоты, выход буферного регистра является цифровым выходом имитатора, а выход цифроаналогового преобразователя - аналоговым выходом имитатора.

Предлагаемое техническое решение поясняется чертежами.

На фиг. 1 представлена структурная схема предлагаемого устройства, на фиг. 2 - трехмерные диаграммы матриц переходных вероятностей гауссовского случайного процесса с различными коэффициентами корреляции, на фиг. 3 - их трехмерные диаграммы функций распределения вероятностей гауссовского случайного процесса с различными коэффициентами корреляции, на фиг. 4 - результаты моделирования работы имитатора гауссовского случайного сигнала, на фиг. 5 - слагаемые критерия χ², а на фиг. 6 - зависимости χ² от разрядности генератора псевдослучайных чисел.

Генератор опорной частоты (Г) 1 на первом выходе выдает тактовые импульсы (ТИ1), по которым генератор псевдослучайных чисел (ГПСЧ) 2 формирует D-разрядный равновероятный двоичный код, поступающий на первый вход цифрового компаратора (ЦК) 3, с которым сравнивается D-разрядный заранее вычисленный по заданной двумерной плотности вероятностей двоичный код функции распределения вероятностей F_ij - марковской модели имитируемого процесса, записанный в блоке памяти (БП) 4. В регистре (РГ) 5 содержится полученное на предыдущем шаге имитации m-разрядное двоичное значение случайного сигнала i, которое записывается в него по тактовому импульсу ТИ2 на втором выходе Г 1. На тактовый вход регистра последовательных приближений (РПП) 6 поступает пачка из (m+1) импульсов ТИ3 с третьего выхода Г 1. Первый из ТИ3 устанавливает в РПП 6 код 10…0, поступающий на первый адресный вход 7 БП 4, при этом на втором адресном входе 8 БП 4 присутствует код i с выхода РГ 5, и на выходе БП 4 появляется D-разрядный двоичный код 9 значения F_ij. Коды от ГПСЧ 2 и БП 4 сравниваются в ЦК 3, который формирует управляющий бит для РПП 6. Вторым импульсом ТИ3 от Г 1 в РПП 6 записывается код 110…0, если код на выходе ГПСЧ 2 больше кода на выходе 9 БП 4, в противном случае в РПП 6 формируется код 010…0. Управление осуществляется сигналом с выхода ЦК 3 на управляющем входе РПП 6. Далее процесс повторяется до тех пор, пока предпоследним m-м импульсом ТИ3 будет сформирован младший разряд кода в РПП 6, а затем последним (m+1)-м импульсом ТИ3 m-разрядный код j из РПП 6 записывается в регистр РГ 5 и в буферный регистр БР 10, образуя код имитируемого псевдослучайного числа. Выходной код БР 10 передается на вход цифроаналогового преобразователя ЦАП 11 и на цифровой выход имитатора 12, выходное аналоговое напряжение ЦАП 11 подается на аналоговый выход имитатора 13. После следующего импульса ТИ1 процесс повторяется.

Устройство работает следующим образом.

На основе заданной двумерной плотности вероятностей w(x₁, х₂) имитируемого сигнала формируется однородная марковская модель [6-8], описываемая матрицей переходных вероятностей



где P_ij - вероятность перехода дискретного сигнала от значения z_n=i,

 М=2^m (m- число разрядов двоичного кода отсчета) в момент времени t_n к значению z_n+1=j,   в следующий момент времени t_n+1; n - номер отсчета имитируемого сигнала.

На основе матрицы переходных вероятностей [P_ij] (1) формируется матрица двумерной функции распределения вероятностей



Для стационарного гауссовского случайного процесса x(t), рассматриваемого в моменты времени t₁, t₂, двумерная плотность вероятностей имеет вид [8]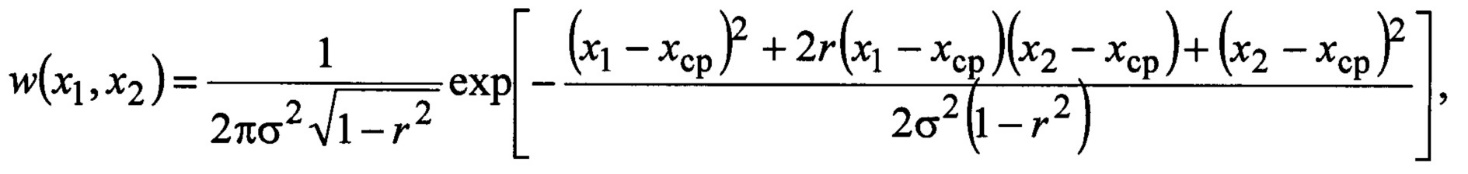



где х_ср - среднее значение, σ² - дисперсия,   - коэффициент корреляции процесса x(t).

Если выбирать шаг квантования по уровню d=(6÷10)σ/М и значения уровней квантования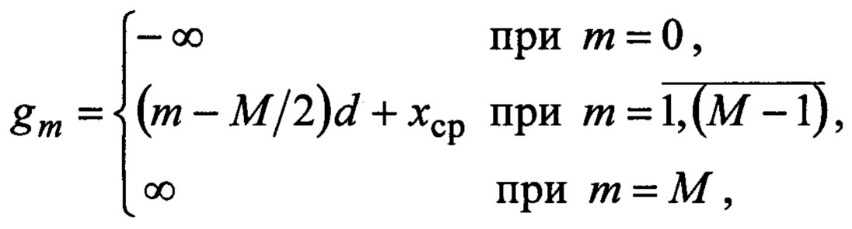



то для переходных вероятностей получим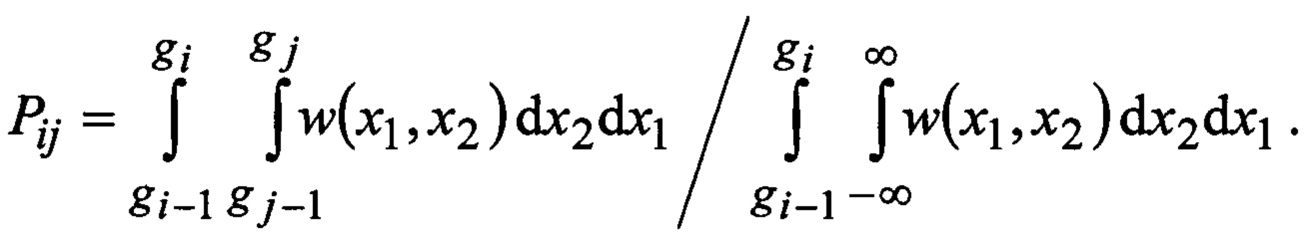



Матрицы [P_ij] и [F_ij] удобно представить графически в трехмерных координатах. Для рассмотренного двумерного гауссовского распределения при x_cp=0, σ=1, М=32 (m=5) и различных коэффициентах корреляции r диаграммы [P_ij] показаны на фиг. 2, а диаграммы [F_ij] - на фиг. 3. Для фиг. 2а и 3а коэффициент корреляции равен 0, для фиг. 2б и 3б коэффициент корреляции равен 0,8, для фиг. 2в и 3в коэффициент корреляции равен - 0,8.

Аналогичная марковская модель может быть построена по экспериментальной реализации сигнала достаточно большого объема N. Для оценки P_ij определяются числа 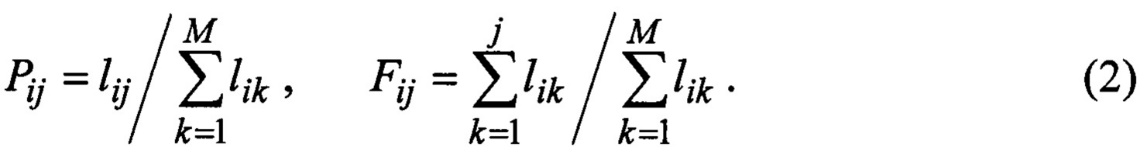  переходов соседних отсчетов сигнала от z_n=i к z_n+1=j. Тогда при большом объеме выборки N»М² получим оценки



Для устранения возможной неопределенности оценок (2) к значениям   целесообразно добавить константу, например, 1.

Вероятности F_ij при любом i с ростом j меняются в пределах от F_i1=0 до F_iM=1. Каждое значение F_ij представляется двоичным D-разрядным кодом G_ij=d_D-1d_{D-2 …} d₀ (от 00…0 до 11…1) и записывается в блок памяти в D-разрядные ячейки с адресами A=i2^m+j А=i⋅2^m+j (где m - разрядность выходных отсчетов имитатора).

Источник равновероятных случайных (псевдослучайных) чисел ГПСЧ 2 может быть реализован в виде шумового генератора [1], или, например, в виде генератора M-последовательности [2] на базе многоразрядного регистра сдвига. Он формирует двоичные D-разрядные коды U=u_D-1 и u_D-2 … u₀. При разрядности регистра сдвига R=43 период М-последовательности равен 2^R-1=8,796⋅10¹², а при R=6l уже 2^R-1=2,306⋅10¹⁸, что вполне достаточно для формирования реализаций случайного сигнала большой длительности. Если используется шумовой генератор, то имитатор будет формировать «истинно» случайные числа.

По тактовому импульсу ТИ1 ГПСЧ 2 формирует код U=u_D-1 u_D-2 … u₀, поступающий на первый вход ЦК 3. В регистре РГ 5 записано значение i отсчета, полученное на предыдущем цикле работы имитатора (его начальное состояние может быть любым). После ТИ1 первым импульсом ТИ3 в РПП записывается код 10…0 (среднее значение m-разрядного кода отсчета j) и из блока памяти БП 4 на его выходе 9 появляется код G_ij=d_D-1d_D-2 … d₀, поступающий на второй вход ЦК 3. Цифровой компаратор ЦК 3 является вычитателем двоичных кодов. Если в БП 4 записать дополнительные коды чисел G_ij, то в качестве ЦК 3 можно использовать двоичный сумматор.

Знаковый разряд ЦК 3 управляет работой РПП 6. Если код U от ГПСЧ 2 больше кода G_ij=d_D-1d_D-2 … d₀, то вторым импульсом ТИ3 в РПП 6 записывается код 110…0, а иначе код 010…0. Далее процесс продолжается аналогично, пока в РПП 6 после m импульсов ТИ3 не сформируется m-разрядный коду.

Регистр последовательных приближений описан в [9]. На его основе строятся аналого-цифровые преобразователи последовательных приближений, что на практике может быть реализовано применением отдельной интегральной схемы РПП К155ИР17.

Тактовым импульсом ТИ2 полученный в РПП 6 код j записывается в регистр РГ 5, становясь предшествующим отсчетом i, и в буферный регистр БР 10, с выхода которого отсчеты случайного сигнала выдаются на цифровой выход 12, а через ЦАП 11 - на аналоговый выход 13.

С целью проверки работоспособности и эффективности предложенного генератора было проведено моделирование его работы при формировании отсчетов случайного гауссовского сигнала с параметрами х_ср=0, σ=1, М=32 и коэффициентом корреляции между двумя соседними отсчетами r=0,8. На фиг.2б и 3б приведена марковская модель моделируемого процесса: трехмерные диаграммы матрицы переходных вероятностей P_ij и функции распределения вероятностей F_ij. На фиг. 4а показана сгенерированная имитатором временная диаграмма отсчетов сигнала x_n (где n - номер отсчета), на фиг. 4б - гистограмма сгенерированной выборки (где также пунктиром изображена соответствующая теоретическая плотность вероятности гауссовского распределения), а на фиг. 4в - зависимость коэффициента корреляции r_k=〈x(t₁)x(t_k)〉 от смещения отсчетов k (где пунктиром нанесена теоретическая зависимость r_k).

При заданной разрядности m имитируемых случайных чисел точность вероятностных характеристик зависит от разрядности D кодов G_ij=d_D-1d_D-2 … d₀ и U=u_D-1u_D-2 … u₀. Для количественной оценки точности имитации вероятностных характеристик воспользуемся критерием согласия χ² (Пирсона) [10]: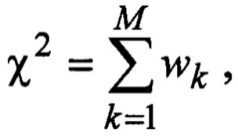



где



n_k - число значений x_k=k отсчетов в выборке объема N (ее гистограмма),

P_k - теоретическое значение вероятности появления x_k (одномерное распределение вероятностей). Величины w_k (3) характеризуют отклонение гистограммы от теоретического значения для k-го значения отсчета. На фиг. 5 показаны полученные в результате статистического имитационного моделирования зависимости w_k от (k-1) при М=64, N=2²⁰≈10⁶ и различной разрядности D кода значений F_ij. Фиг. 5а соответствует D=11 (χ²=219), фиг. 5б - D=14(χ²=71). Как видно, w_k увеличиваются в области маловероятных значений и уменьшаются с ростом D.

Величина χ² характеризует достоверность гипотезы о соответствии эмпирической оценки вероятностей заданному распределению. При заданной значимости а критерия Найквиста вычисляется граничное значение   и, если   то эмпирическое распределение вероятностей соответствует теоретическому.

На фиг. 6 сплошными линиями представлены зависимости χ² от D при М=2⁶=64 (фиг. 6а) и М=2⁸=256 (фиг.6б). Здесь же пунктиром при значимости α=0,01 отмечены величины   соответственно. При М=2¹⁰=1024 значение   достигается уже при D=11. Таким образом, при m=6 необходимо выбрать D=14, при m=8-D=13, а при m=10-D=11, соответственно. При m≥16 можно принять D=m.

Для хранения кодов G_ij=d_D-1d_D-2 … d₀ в предлагаемом имитаторе необходим объем блока памяти БП V1=2^2m D бит. В свою очередь, для реализации прототипа изобретения [5] необходим объем памяти БП V2=2^m+D m бит. Таким образом, величина V2/V1 характеризует выигрыш в емкости блока памяти в предлагаемом техническом решении по сравнению с прототипом. Указанные величины приведены в таблице.



Из полученных результатов следует, что предлагаемый имитатор с высокой точностью формирует случайный сигнал, двумерные статистические свойства которого определяются заданной марковской моделью, и при m≤10 обеспечивает значительный выигрыш в требуемом объеме блока памяти.

ЦИФРОВОЙ ИМИТАТОР СЛУЧАЙНЫХ СИГНАЛОВ

Формула изобретения
Цифровой имитатор случайных сигналов, содержащий генератор опорной частоты, блок памяти, цифроаналоговый преобразователь, генератор равновероятных псевдослучайных чисел и регистр, дополнительно содержит цифровой компаратор, первый вход которого подключен к выходу генератора равновероятных псевдослучайных чисел, второй вход - к выходу блока памяти, регистр последовательных приближений, тактовый вход которого подключен к третьему выходу генератора опорной частоты, управляющий вход - к выходу цифрового компаратора, а выход параллельно соединен с первым адресным входом блока памяти и входом регистра, и буферный регистр, вход которого подключен к выходу регистра последовательных приближений, а выход - к входу цифроаналогового преобразователя, выход регистра соединен со вторым адресным входом блока памяти, а его тактовый вход - со вторым выходом генератора опорной частоты, тактовый вход генератора равновероятных псевдослучайных чисел подключен к первому выходу генератора опорной частоты, выход буферного регистра является цифровым выходом имитатора, а выход цифроаналогового преобразователя - аналоговым выходом имитатора.