ТЭЦ. Отчет о выполнении проектной работы Расчет и исследование переходных процессов в линейных электрических цепях
 Скачать 85.75 Kb. Скачать 85.75 Kb.
|
|
ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра «Электроэнергетика и электротехника» ОТЧЕТ о выполнении проектной работы Расчет и исследование переходных процессов в линейных электрических цепях Выполнил студент гр. 18ПТ1 Шебалков Р.О. отчет принят ________202_ г Преподаватель к.т.н., доцент Регеда О. Н. Пенза, 2020 Введение Процессы, возникающие в электрической цепи при переходе от одного установившегося энергетического режима к другому установившемуся энергетическому режиму, называются переходными процессами (режимами). В установившихся режимах токи и напряжения в электрической цепи определяются только видом действующих в цепи источников энергии. Источники энергии могут быть либо постоянными, либо гармоническими, либо несинусоидальными, но периодическими. В отличие от установившихся режимов, изменение токов и напряжений в электрической цепи во время переходного процесса происходит не периодически. Мгновенные значения токов и напряжений, возникающих в переходных режимах, могут во много раз превысить их установившиеся значения. Это обусловливает важность задачи анализа переходных процессов. Возникновение переходных процессов в электрической цепи связано с коммутациями, т.е. скачкообразного изменения структуры цепи, параметров ее элементов, а также подключением или отключением источников энергии. И хотя изменения не могут происходить мгновенно, что связано с изменением количества энергии, запасенной в электрических и магнитных полях, для упрощения расчетов обычно пренебрегают временем коммутации. Цель проектной работы – анализ и моделирование линейны напряжение и токов в разветвленных электрических цепях, работающих в переходных режимах и проверка их соответствия теоретическим значениям. 1 Расчет переходных процессов в линейных электрических цепях Рассчитаем переходный процесс при смешанном соединении элементов (рисунок 1). Найдем закон изменения тока через индуктивность i(t), если до коммутации ключ был в положении 2, а после коммутации в положении 1. Расчет проведем для следующих значений параметров R1 = 21 Ом, R2 = 41 Ом, R3 = 71 Ом, E = 11 В, L = 6 мГн. 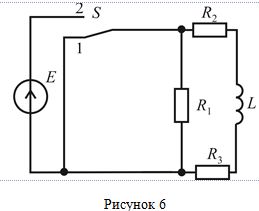 Цепь 1) Анализ цепи до коммутации показывает, что независимые начальные условия для неё – это ток через индуктивность i(t). На рисунке 2 представлена цепь до коммутации (XL=0, так как f = 0 на постоянном токе).  Цепь до коммутации R23=R2+R3=112 Ом R123=R1*R23/R1+R23=2352/133=17,68 Ом iL(0-) = E/R123 = 11/17,68=0,622 А, Uab(0-) = iL(0-)* R123 = 0,622*17,68 = 10,99 В, iL(0-) = iL(0+) = Uab(0-)/R1 = 10,99/21 = 0,523 А. 2) Найдем операторное сопротивление для этой цепи после коммутации. Цепь после коммутации представлена на рисунке 3.  Цепь после коммутации Z(p) = R2+pL+R3= 112 Ом Найдем корень характеристического уравнения и постоянную времени цепи как: R2+pL+R3 = 0, 41+0,006p+71 = 0, p = 112/-0,006 ≈ -18666 c-1, τ = -1/p = 1/18666 = 0,00005 мс. 3) Свободная составляющая тока равна: iLсв =Aept = Ae-t/τ А. 4) Принужденная составляющая тока в данной цепи будет равна 0, так как нет источника ЭДС: iLпр = 0 А. 5) Таким образом, общее решение для тока в цепи в амперах равно: iL= Aept + 0 А. 6) Для нахождения постоянной интегрирования А запишем последнее выражение в момент времени t=0+ и с учетом независимых начальных условий на основании первого закона коммутации получим: iL= A = 0,523 А. Общее решение дифференциального уравнения для тока запишется как: iL(t) = 0,523e-18666/3t А. График изменения тока для рассмотренной цепи показан на рисунке 4. 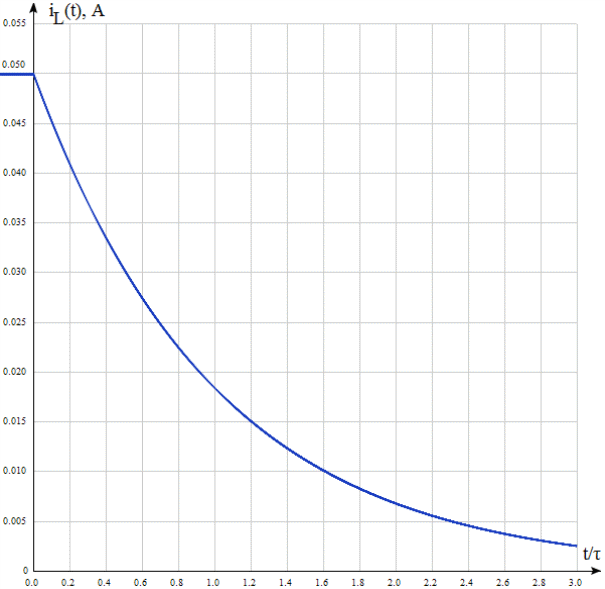 Изменение тока Анализ результатов и вывод. Анализ полученного графика показывает, что в соответствии с первым законом коммутации ток через индуктивность не меняется скачком. |
