Отчет по геодезо практике по геодезии. Отчет по геодезической практике
 Скачать 3.91 Mb. Скачать 3.91 Mb.
|
|
Из решения обратных геодезических задач по дирекционным углам исходных направлений и значениям примычных углов вычислен дирекционный угол линии теодолитного хода А-1: αА1 = 117о42'15,2". Аналогичные вычисления дирекционных углов линий теодолитного хода при его азимутальной привязке были выполнены при обработке разомкнутого теодолитного хода. В данном случае необходимо определить только значение дирекционного угла одной линии теодолитного хода. Пример обработки ведомости координат замкнутого теодолитного хода приведен в табл. 9. Таблица 9 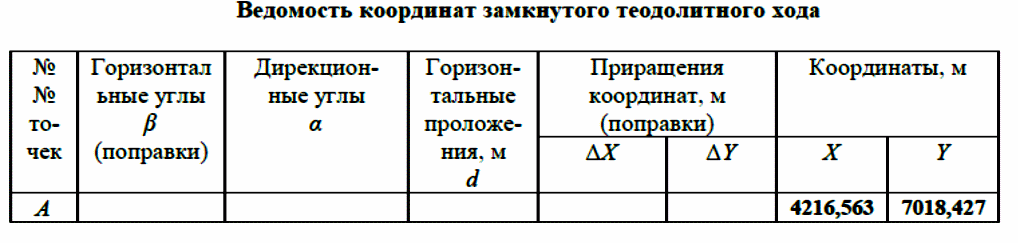 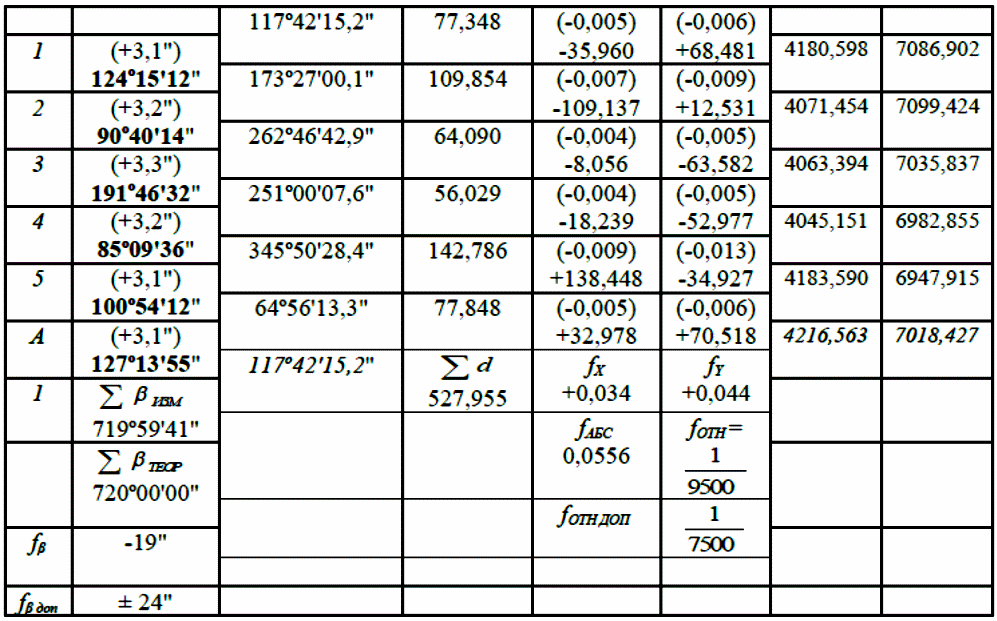 Оценка точности угловых измерений и вычисление дирекционных углов В замкнутом теодолитном ходе (полигоне) могут быть измерены внутренние, либо внешние горизонтальные углы β (рис. 12). Если принять направление обхода по часовой стрелке, то все внутренние горизонтальные углы, показанные на схеме, будут правыми по ходу. Теоретическая сумма горизонтальных углов замкнутого многоугольника равна: - для внутренних углов: Σβтеор= 1800(n - 2) ; (27) - для внешних углов: Σβтеор = 1800(n + 2) , (28) где n – число измеренных внутренних или внешних углов. Угловая невязка в этом случае может быть определена по формуле fβ = Σβизм - Σ. (29) В дальнейшем обработка результатов угловых измерений подобна обработке результатов угловых измерений разомкнутого теодолитного хода: вычисление допустимой угловой невязки по формуле (6); проверка условия (7); вычисление поправок в углы и контроль их вычисления по формулам (8) и (9); исправление углов по формуле (10) и контроль исправления по соблюдению равенства ΣβТЕОР = ΣβИСПР. (30) Дирекционные углы линий замкнутого теодолитного хода вычисляют последовательно по ходу с контрольным вычислением дирекционного угла его линии, вычисленного при азимутальной привязке. Так, следуя обозначениям на схеме рис. 7.26 и принятому направлению хода, α12 = αА1исх ± 180 – β1ИСПР α23 = α12 ± 180 – β2ИСПР α34 = α23 ± 180 – β3ИСПР α45 = α34 ± 180 – β4ИСПР α5А = α45 ± 180 – β 5ИСПР αА1выч = α5А ± 180 – βА ИСПР (31) Контрольное значение дирекционного угла, полученное по последнему выражению формул (31) для линии А1 должно точно соответствовать его исходному значению. Вычисление приращений координат и оценка точности хода Поскольку начальная и конечная точки замкнутого теодолитного хода совмещены, то, как следует из формул (15), теоретические суммы приращений координат, вычисленных из решения прямой геодезической задачи, должны быть равны нулю, т.е. ΣΔХТЕОР = 0 ΣΔYТЕОР = 0 (32) а невязки в приращениях координат определятся только суммами полученных соответствующих приращений fх = ΣΔХВЫЧ fy = ΣΔYВЫЧ (33) Далее оценка точности хода заключается в вычислении абсолютной невязки хода (18), относительной невязки хода (19) и в сравнении последней с допустимой относительной невязкой, установленной для данного вида работ соответствующей инструкцией или техническим заданием. По аналогии с разомкнутым теодолитным ходом физический смысл невязок в приращениях координат тот же (рис. 11 б). Уравнивание приращений координат и вычисление координат точек хода Поправки в приращения координат (весовые) вычисляются по формулам (22) с контролем их вычислений по формулам (23). Контрольные суммы исправленных (24) приращений координат для замкнутого теодолитного хода должны быть равны нулю, т.е. ΣΔХИСПР = 0 ΣΔYИСПР= 0. (34) Координаты точек вычисляют последовательно по ходу по принятому ранее направлению с контрольным замыканием на начальную точку хода: 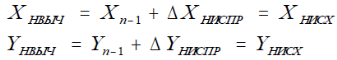 (35) (35)Теодолитная съемка Съемка – комплекс работ, которые выполняют на местности с целью получения оригинала топографической карты или плана, а также получения топографической информации в другом виде, например, цифровом. В результате выполнения теодолитной съемки получают плановое положение контуров и местных предметов. Теодолитная съемка обычно производится сравнительно на небольших участках местности, изображаемых в последующем на топографических планах крупных масштабов. Геодезической основой для теодолитной съемки являются теодолитные ходы, сгущаемые от пунктов Государственной геодезической сети 1-4 классов, а также пунктов сетей 1 и 2 разрядов. Формы ходов зависят от характера снимаемой местности. Так, при съемке площадных объектов целесообразно использовать замкнутые ходы в сочетании с диагональными и висячими ходами, при съемках линейных сооружений – разомкнутые в сочетании, в основном, с висячими ходами.. Теодолитная (горизонтальная, плановая) съемка выполняется при помощи теодолита и мер длины (лента, рулетка) или дальномеров. Предельная погрешность (mS) положения пунктов плановой съемочной сети относительно пунктов ГГС или ГСС не должна превышать 0,2 мм в масштабе плана. Теодолитные ходы прокладываются с предельными относительными по- грешностями 1:3000, 1:2000, 1:1000 в зависимости от условий съемки (см.табл.10) Таблица 10 Допустимые относительные погрешности в теодолитных ходах 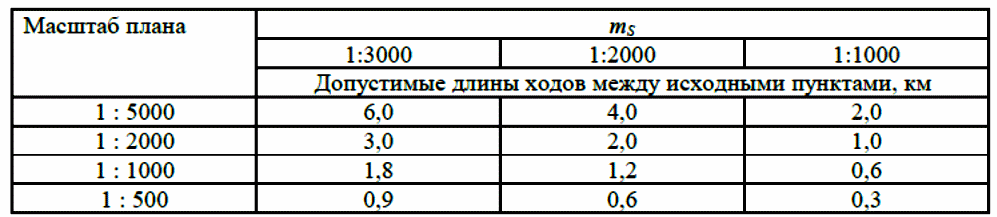 Теодолитная съемка ситуации выполняется способами угловой и линейной засечек, полярных координат, перпендикуляров, обхода, створов и комбинированными способами. 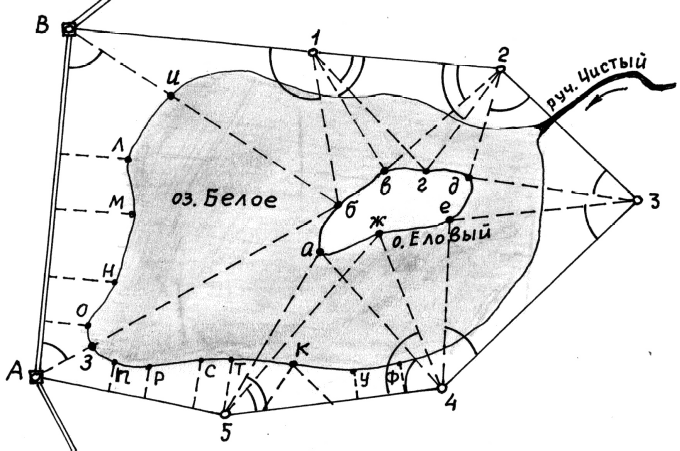 Рис. 13. Способы теодолитной съемки 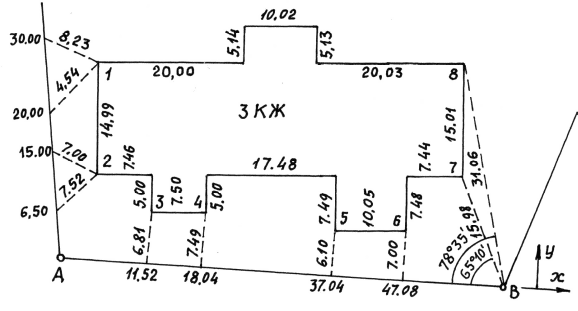 Рис.14. Способы теодолитной съемки Способ угловой засечки используют для съемки точек, недоступных для непосредственных измерений. На план снятые точки наносят графически, либо по координатам, предварительно вычисленным по формулам Юнга. В частности, указанный способ использован для получения положения острова (точки а – ж) – рис. 14. Вокруг озера проложен для выполнения съемки способом обхода замкнутый теодолитный ход, привязанный к основной геодезической основе АВ. На рис. 13 способом линейной засечки получено положение точки к, находящейся на берегу озера. На рис. 14 таким же способом получено положение точек 1 и 2 здания. Обычно точки местности, полученные способом линейной засечки, наносят на план графически по соответствующим расстояниям. Способ полярных координат применяют для съемки точек, находящихся в прямой видимости сравнительно недалеко от точек и линий теодолитного хода. При этом целесообразно, чтобы измеряемые расстояния не превышали длины мерного прибора (ленты или рулетки). При больших углах наклона в измеренное расстояние вводят поправку за наклон для получения горизонтального проложения. На рис. 13 таким способом получены точки и и з одновременно с выполнением угловой засечки. На рис. 14 указанный способ использован для съемки точек 7 и 8 сооружения. Точки на план наносят графически по значению горизонтального угла и горизонтального проложения, либо по координатам, предварительно вычисленным из решения прямой геодезической задачи с точек съемочного обоснования. Если съемочные точки находятся вблизи от линии съемочного обоснования, то удобно использовать для их съемки способ перпендикуляров (прямоугольных координат). На рис. 13 таким способом получено положение точек л – ф береговой линии озера, а на рис. 14 – точки 3, 4, 5 и 6 здания. Часто линию съемочного обоснования принимают за ось х, а перпендикулярную к ней линию – за ось y условной системы координат. При этом значения координат х и y съемочных точек могут быть положительными и отрицательными. Результаты измерений оформляют в виде таблицы и соответствующего абриса, похожего на приведенные рисунки, с полным указанием на нем результатов измерений и привязок к точкам и линиям съемочного обоснования. Абрис составляют обычно на одну из линий съемочного обоснования, либо на две-три таких смежных линии. Точки, полученные способом перпендикуляров, наносят на план графически. Способ обхода чаще используется для съемки контуров, имеющих значительную площадь. Вокруг контура прокладывают дополнительный замкнутый теодолитный ход и с точек и линий этого хода любыми известными способами получают положение искомых точек. Ответственные точки местности часто снимают повторно с других станций, либо на той же станции, но другим способом (комбинированный способ съемки). Комбинированный способ съемки может быть реализован, например, одновременным получением координат точки способом угловой и линейной засечек при использовании электронных тахеометров. Если линия съемочного обоснования пересекает контур объекта местности, линейный контур сооружения, то положение точки пересечения фиксируют промерами в створе линии съемочного обоснования. Такой способ называют способом створов. Часто створ задают отдельно от линии съемочного обоснования направлением, а положение точек местности от него получают способом перпендикуляров. При съемках зданий обязательно производят полные их обмеры. Это позволяет пополнить недостающие элементы контура здания, а также является надежным контролем результатов съемки. Контрольные промеры выполняют и между точками твердых контуров, полученных с разных станций, либо с одной станции, но независимо от другой точки. Такие промеры могут быть выполнены между углами двух соседних зданий, между углами одного и того же здания сложной конфигурации, между точкой-ориентиром и углом здания и т.п. Горизонтальные углы при теодолитной съемке измеряют теодолитом полным приемом, во многих случаях и расстояния измеряют дважды – в прямом и обратном направлениях, если они значительно превышают длину мерного прибора. Центрирование теодолита в точке съемочного обоснования должно обеспечить необходимую точность измерения горизонтальных углов. Вычисления координат вершин теодолитного хода Невязка углов хода Σβпр = 239°43' + 237°12' + 358°30' + 244°37' = 1080°2' Σβт = 180° * (n + 2) = 180° *(4+2) = 1080°00’00” – внешние углы f β = Σβпр – Σβт = 1080°2' - 1080°0’ = 0°2’0” Вычисление дирекционных углов и румбов сторон хода αn = αn-1 + β1 -180° α1-2 = 63°17'0,7" + 239°42'30" - 180° = 122°59,5' α2-3 = 122°59,5' + 237°11'30" - 180° = 180°11' α3-4 = 180°11' + 358°29'30" - 180° = 358°40,5' α4-5 = 358°40,5' + 244°36'30" - 180° = 63°17' Вычисление румбов + + I 0° - 90° СВ 1) r 1-2 = 180° - 122°59,5' = 57°0,5' (ЮВ) - + II 90° - 180° ЮВ 2) r 2-3 = 180°11' - 180° = 0°11' (ЮЗ) - - III 180° - 270° ЮЗ 3) r 3-4 = 360° - 358°40,5' = 1°19,5' (СЗ) + - IV 270° - 360° СЗ Вычисление приращений координат Δx = ± d * cosr ; Δy = ± d * sinr Δx 1-2 = 18,528 * cos 63°17'0,7" = + 8,33 (м) Δy 1-2 = 18,528 *sin 63°17'0,7" = + 16,55 (м) Δx 2-3 = 17,673 *cos 57°0,5' = - 9,62 (м) Δy 2-3 = 17,673 *sin 57°0,5' = + 14,82 (м) Δx 3-4 = 17,079 * cos 0°11' = -17,08 (м) Δy 3-4 = 17,079 * sin 0°11' = - 0,05 (м) Δx 4-5 = 12,423 * cos 1°19,5' = + 12,42 (м) Δy 4-5 = 12,423 * sin 1°19,5' = - 21,72 (м) Δx 5-1 = 22,407 * cos 63°17' = +10,07 (м) Δy 5-1 = 22,407 * sin 63°17' = + 20,01 (м) Невязка координат Δx, Δy = 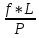 Для Δx: Для Δy: 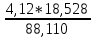 = 0,86 1) = 0,86 1) 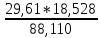 = 6,22 = 6,22 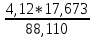 = 0,82 2) = 0,82 2)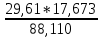 = 5,94 = 5,94 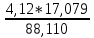 = 0,79 3) = 0,79 3)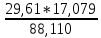 = 5,73 = 5,73 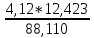 = 0,58 4) = 0,58 4)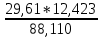 = 4,17 = 4,17 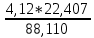 = 1,04 5) = 1,04 5)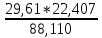 = 7,53 = 7,53
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
