Индивидуальные задания. Отчет по индивидуальному заданию 1, 2 по дисциплине Конечные автоматы и логические сети

• Название: Отчет по индивидуальному заданию 1, 2 по дисциплине Конечные автоматы и логические сети
• Дата: 15.01.2021
• Размер: 461 Kb.
• Имя файла: Индивидуальные задания.doc
• Тип: Отчет; #168475
• страница: 2 из 4

2.2 Минимизация полученной функции

Карту Карно, используемую для минимизации, представим на рисунке 1

		0 0	0 1	1 1	1 0
		a` b`	a` b	a b	a b`
0 0	c` d`	1	1	0	1
0 1	c` d	1	1	1	1
1 1	c d	0	0	1	1
1 0	c d`	0	0	0	0

Рисунок 1 – минимизация функции с помощью карт Карно
В результате минимизации нами было получено следующее выражение для булевой функции




F (a,b,c,d) =ac ⅴ ad ⅴ bc

2.3 Построение полученной минимизированной функции в смешанном базисе

Представим полученную минимизированную функцию .Проверим полученную логическую схему, построив ее модель в программе «Electronic Work Bench 5.1». Результат построения представим на рисунке 2.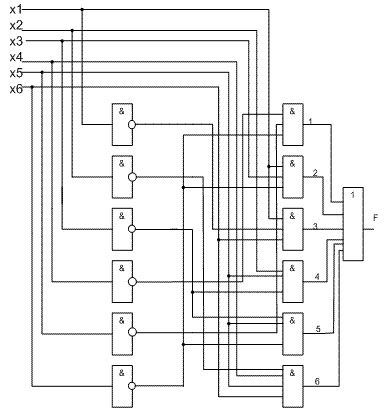


Рисунок 2 – Проверка реализации функции в смешанном базисе

3 Анализ заданной комбинационной схемы

3.1 Получение таблицы истинности булевой функции, заданной логической схемой

Нам задана логическая схема, изображенная на рисунке 3.



Рисунок 3 – Логическая схема
Построим по заданной схеме таблицу истинности. Для этого воспользуемся следующим алгоритмом:

1. 
   проведем анализ сумматора и выясним, какие конъюнкты входят в его состав;
   
2. 
   проведем анализ вычлененных конъюнктов, выясним какие переменные входят в каждый конъюнкт и посчитаем значения функции на выходе каждого из них;
   
3. 
   проведем логическую суммацию полученных значений и получим в итоге значения функции на выходе сумматора. На рисунке 4 представим графическую интерпретацию наших рассуждений.
   

Рисунок 4 – Вычленение наборов элементарных логических элементов
Т.к. заданная логическая схема состоит из набора, представленного элементарными логическими элементами, при анализе схемы определим значения составных частей функции, которые реализуют каждый из элементарных логических элементов в точках А, B, C, D, E, G и определим итоговую функцию F(a, b, c, d).

Результат вычислений представим в таблице 2.
Таблица 2 – Таблица истинности

a	b	c	d	A=abc	B=abd`	C=ab	D=a`b`c	E=abcd	G= bd`	F(a,b,c,d)
0	0	0	0	0	0	0	0	0	0	0
0	0	0	1	0	0	0	0	0	0	0
0	0	1	0	1	0	0	0	0	0	1
0	0	1	1	1	0	0	0	0	0	1
0	1	0	0	0	0	0	0	0	0	0
0	1	0	1	0	0	0	0	0	0	0
0	1	1	0	0	0	0	0	0	0	0
0	1	1	1	0	0	0	0	0	0	0
1	0	0	0	0	0	1	1	0	0	1
1	0	0	1	0	0	1	0	1	0	1
1	0	1	0	0	0	1	0	0	0	1
1	0	1	1	0	0	1	0	1	0	1
1	1	0	0	0	1	0	1	0	0	1
1	1	0	1	0	0	0	0	0	0	0
1	1	1	0	0	1	0	0	0	1	1
1	1	1	1	0	0	0	0	0	1	1