Индивидуальные задания. Отчет по индивидуальному заданию 1, 2 по дисциплине Конечные автоматы и логические сети

• Название: Отчет по индивидуальному заданию 1, 2 по дисциплине Конечные автоматы и логические сети
• Дата: 15.01.2021
• Размер: 461 Kb.
• Имя файла: Индивидуальные задания.doc
• Тип: Отчет; #168475
• страница: 4 из 4

4.2 Построение минимизированной функции в смешанном базисе

Реализуем полученную функцию на логических элементах в смешанном базисе. Представим ее в приложении А. Проверим полученную логическую схему, построив ее модель в программе «Electronic Work Bench 5.1». Результат построения представим на рисунке 6.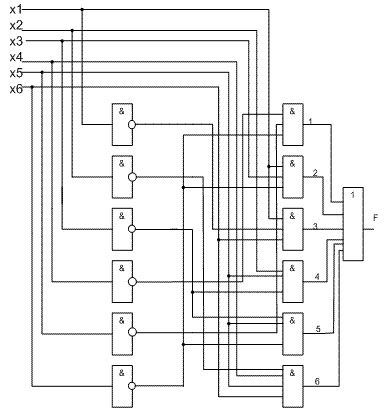


Рисунок 6 – Проверка реализации функции в смешаном базисе

4.3 Построение минимизированной функции в базисе «2-и-не»

Для реализации функции в базисе «2-и-не» представим минтермы в сгруппированном виде по две переменные. В тех элементах, в которых входы останутся свободными, будем подавать единицу чтобы не изменить логическое значение элемента на выходе. Реализуем функцию на логических элементах в базисе «2-и-не». Проверим полученную логическую схему, построив ее модель в программе «Electronic Work Bench 5.1». Результат построения представим на рисунке 7



Рисунок 7 – Проверка реализации функции в базисе «2-и-не»

4.4 Представление минимизированной функции в базисе «4-или-не»

Для реализации функции в базисе «4-или-не» каждый элемент «ИЛИ» будет преставлять один минтерм, так как колическтво переменных в каждом минтерме не превышает заданного количества входом в логических элементах.. Проверим полученную логическую схему, построив ее модель в программе «Electronic Work Bench 5.1». Результат построения представим на рисунке 8.



Рисунок 8 – Проверка реализации функции в базисе «4-или-не»

4.5 Построение минимизированной функции с использованием дешифратора

Реализуем функцию с использованием восьмиканального дешифратора, с каскадным методом подключения (один управляющий и восемь вспомогательных дешифраторов).

Каждому цифровому коду на выходах дешифратора соответствует логическая 1 (или логический 0) на соответствующем выходе. Иными словами, каждый входной код адресует соответствующий выход, который при этом возбуждается. Поэтому входы дешифратора часто называют адресными. Стоящие возле них цифры (1,2,3,4…) показывают как соотносятся веса разрядов поступающего двоичного числа.

Выходы дешифратора оцифрованы десятичными числами. Возбуждается тот выход, номер которого равен весу входного кода, разряды которого имеют обозначенные веса, т.е. дешифратор расшифровывает (дешифрирует) число, записанное в двоичном коде, представляя его логической 1 (логическим 0) на соответствующем выходе.

Для реализации каскадного метода запишем СДНФ нашей функции

СДНФ = X’6X’5X’4X’3X2X’1 V X’6X’5X’4X3X2X1 V X’6X’5X4X3X’2X1 V X’6X’5X4X3X2X1 V X’6X5X’4X’3X’2X1 V X’6X5X’4X3X’2X1 V X’6X5X4X’3X’2X1 V X’6X5X4X’3X’2X’1 V X’6X5X4X’3X’2X1 V X’6X5X4X3X2X1 V X6X’5X’4X’3X’2X’1 V X6X’5X’4X’3X’2X1 V X6X’5X’4X3X’2X’1 V X6X’5X’4X3X’2X1 V X6X’5X4X’3X2X’1 V X6X5X’4X’3X’2X’1 V X6X5X’4X3X2X’1 V X6X5X4X’3X’2X’1 V X6X5X4X’3X2X’1 V X6X5X4X3X2X’1.
Далее проводим анализ СДНФ:

1. 
   рассмотрим старшие три разряда нашей функции - x₁, x₂, x₃. Если они представлены в СДНФ всеми восемью десятичными цифрами от нуля до семи, то в схеме каскадного подключения будут использоваться все восемь вспомагательных дешифраторов, если какое-то из десятичных значений отсутствует, то соответствующий ему дешифратор из схемы удаляется;
   
2. 
   от соответствующих выходов упраляющего дешифратора подаем сигналы на управляющее входы вспомагательных дешифраторов;
   
3. 
   рассмотрим теперь три младших разряда нашей функции – x₄, x₅, x₆. На каждом вспомогательном дешифраторе будем задействовать только те выходы, для которых комбинация наборов трех старших и трех младших разрядов присутствует в СДНФ.
   

Проверим полученную логическую схему, построив ее модель в программе «Electronic Work Bench 5.1». Результат построения представим на рисунке 9


Рисунок 9 – Проверка реализации функции в базисе с использованием каскадного подключения дешифраторов

4.6 Построение минимизированной функции с использованием мультиплексора

Реализуем функцию, исплользуя восьмиканальный мультиплексор, с каскадным методом подключения (один управляющий и восемь вспомагательных мультиплексоров). Каждому информационному входу мультиплексора присваивается номер, называемый адресом.

Каскадная схема мультиплексоров реализуется по следуещему алгоритму:

1. 
   строим СДНФ нашей функции;
   
2. 
   на адресные входы управляющего мультиплексора подаем значения трех старших разрядов функции (от младшего к старшему);
   
3. 
   на адресные входы вспомогательных мульплексоров подаем значения трех младших разрядов функции (от младшего к старшему);
   
4. 
   соответствующие выходы вспомагательных мультиплексоров соединяем с соответствующими входами данных управляющего мультиплексора;
   
5. 
   на входы данных мы подаем либо эквивалентный ноль, либо эквивалентную единицу, в зависимости от того – входят ли соответсвующие наборы трех младших разрядов в СДНФ;
   

Проверим полученную логическую схему, построив ее модель в программе «Electronic Work Bench 5.1». Результат построения представим на рисунке 10.


Рисунок 10 – Реализация функции на мультиплексорах при каскадном

Подключении.

Заключение

В ходе выполнения расчетно-графического задания нами был проведен анализ и синтез ряда булевых функций и логических сетей. Случайно задана функция от шести переменных и проведен ее синтез. Была проведена базис с использованием каскадного подключения дешифраторов и базис с каскадным подключением мультиплексоров. Так же был проведен синтез функции, заданной своей ДНФ. Для чего была получена каноническая сумма минтермов, проведена ее минимизация, по которой была построена схема в смешанном базисе. В ходе выполнения работы была задействована программа Electronic Workbench 5.1. Данный программный продукт очень удобен в использовании для проверки правильности построения логических схем. В ходе работы нами были получены навыки по работе с картами Карно, практические навыки по построению логических сетей.

Лист