Индивидуальные задания. Отчет по индивидуальному заданию 1, 2 по дисциплине Конечные автоматы и логические сети
 Скачать 461 Kb. Скачать 461 Kb.
|
3.1 Минимизация полученной булевой функцииКарту Карно, используемую для минимизации, представим на рисунке 3
Рисунок 3 – минимизация функции с помощью карт Карно В результате минимизации нами было получено следующее выражение для булевой функции   F (a,b,c,d) =ab ⅴ ac ⅴ ad F (a,b,c,d) =ab ⅴ ac ⅴ ad3.2 Построение полученной минимизированной функции в смешанном базисеПредставим полученную минимизированную функцию. Проверим полученную логическую схему, построив ее модель в программе «Electronic Work Bench 5.1». Результат построения представим на рисунке 4. 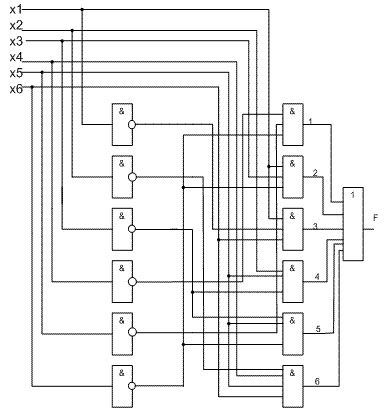 Рисунок 4 – Проверка реализации функции в смешанном базисе 4 Синтез комбинационной схемы случайно заданной логической функции4.1 Построение таблицы истинности и минимизация функции для задания №1Составим таблицу истинности, задав 20 нулей и 20 единиц случайным образом (в «*» функция не определена). Представим её в таблице 2. Таблица 2 – Таблица истинности
В данной работе минимизируем функцию с помощью Карт Карно. Результат минимизации представлен на рисунке 1. Для минимизации функции необходимо следовать, следующим правилам: а) заданная функция преобразуется в СДНФ; б) каждая конституента единицы отмечается 1 в соответствующей клетке Карт Карно; в) единица расположенная рядом или симметрично на краях карты, или симметрично относительно центральных осей, покрываются правильными прямоугольниками, при этом выполняется требование: число m, покрываемых единичных прямоугольников должно быть равно 2k, где k=1,2,…n. Каждый прямоугольник должен покрывать как можно больше значений 1, а количество покрывающих прямоугольников должно быть как можно меньше. Одна и та же единица может быть покрыта разными прямоугольниками; г) для каждого прямоугольника записываем конъюнкцию, в которую должны войти переменные, которые являются общими для 1, покрытых этим прямоугольником; д) записываем минимизированную ДНФ, в которую должны войти конъюнкции соответствующие всем покрывающим прямоугольникам. Если в карте оказалась единица, изолированная от других единиц, то в ДНФ добавляется полностью соответствующая ей конституэнта единицы; е) если есть возможность, сокращаем минимизированную ДНФ путем вынесения переменных за скобки. Покроем области, на которых функция принимает единичные значения или неопределенные значение так, чтобы количество единиц и неопределенных значений было равно 2X, где X – целое число. Карта Карно, используемая для минимизации, представлена на рисунке 5
Рисунок 5 – минимизация функции с помощью карт Карно В результате минимизации нами было получено следующее выражение для булевой функции . F = х’4х’5х’6 V х1х3х’6 V х’1х2х6 V х1х’3х5 V х’3х5х’6 V х’2х4х5х6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 b
b



 1x2x3
1x2x3