Лабораторная работа по Алгоритмам и структурам данных. Курсова работа по АиСД. Палунин Артем. Отчет по Курсовой работе по дисциплине Алгоритмы и структуры данных Тема Графы Студент гр. 9891 Палунин А. И. Преподаватель
 Скачать 176.26 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра вычислительной техники отчет по Курсовой работе по дисциплине «Алгоритмы и структуры данных» Тема: Графы
Санкт-Петербург 2021 Задание: Необходимо в заданном графе найти подграфы, которые будут изоморфны другому заданному графу. В данном случае изначальный граф может быть неограниченных размеров, а граф, которому мы будем искать изоморфный подграф будет всегда одного размера. Содержание: Выбор и обоснование представления данных: 4 Алгоритм программ 5 Иллюстрация работы программы 6-7 Выводы 8 Список используемой литературы 9 Приложение А. Код программы 10-28 Выбор и обоснование представления данных: Так как стоит задача поиска изоморфных ориентированных подграфов, то удобнее всего использовать представление в виде матрицы инцидентности, где строки будут равны узлам графа, а столбцы ребрам графа (0 напротив вершины означает, что ребро не соединяется с данной вершиной, 1 напротив вершины означает, что ребро выходит из данной вершины, -1 напротив вершины означает, что ребро входит в данную вершину). Исходя из этого в столбцах может быть только два ненулевых значения, так как одно ребро может принадлежать только двум вершинам. Почему матрица инцидентности удобнее на мой взгляд? Потому что поиск изоморфных графов — это задача на перебор всех возможных вариантов, а перебирать варианты проще перестановкой строк и столбцов, чем работа со списками. Об алгоритме рассказано будет ниже. Алгоритм работы программы При запуске, программа потребует ввод размера матрицы инцидентности. В которой будет случайным образом сгенерирован граф по следующим условиям: в столбце не больше 2ух ненулевых значений (меньше может быть, так как из вершины могут выходить ребра, а могут не выходить и тогда вершина будет изолирована). Поэтому после того как будет задан размер матрицы massive (тип short**) выделяем память под неё и заполняем нулями. После этого используя функцию rand() генерируем числа temp_1 и temp_2 в интервале от нуля до максимального размера строки графа. После получения значений мы в ячейку массива massive с индексом [i][temp_1] и [i][temp_2] поставим -1 и 1 соответственно. Где i – ‘это номер строки, который увеличивается в цикле for(). Таким образом будет построен произвольный граф. Аналогичным образом строится и матрица второго графа, изоморфные которому будем искать в первом графе. Для удобства обозначений введем следующие понятия: Г_1 (большой граф в котором ищем изоморфные подграфы), Г_2 (маленький граф, изоморфные которому будем искать в Г_1). Г_2 будет всегда размера 3х3, потому что увеличение размера графа будет приводить к увеличению времени поиска, а алгоритм от этого не изменится. Поэтому будем рассматривать поиск изоморфных подграфов для матрицы 3х3. Алгоритм поиска изоморфного подграфа: Алгоритм строится на сравнении подматриц Г_1 размером 3х3 и матрицы Г_2. Для этого в Г_1 на каждой итерации будем выбирать подматрицу 3х3 начиная с левого верхнего угла и двигаясь влево на один столбец на каждой итерации, по окончании столбцов, сдвигаемся на строку вниз и начинаем перемещаться по столбцам вправо и так пока граф не кончится или не найдем изоморфный подграф. Далее пойдем по пунктам: А) После того как выделили первую подматрицу из Г_1, подсчитываем в ней количество 1, 0, -1 и сравниваем с количеством 1, 0, -1 в матрице Г_2. В случае, если их количество отличается мы делаем вывод, что эти графы не могут быть изоморфными, так как нарушается одно из требований, а именно: количество вершин и ребер должно быть равным. Б) Если всё-таки условие равенства вершин и ребер выполняется. Программа начинает перебор 36 вариантов подматрицы. Перестановки реализованы следующим образом: сначала меняем столбцы в такой последовательности: 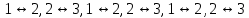 и после каждой перестановки подматрица Г_1 сравнивается с матрицей Г_2. Если до окончания этих 6ти перестановок матрицы не стали равны. То меняем строки и повторяем перебор столбцов. Смена строк происходит аналогично смене столбцов. В) Если на одно из итераций подматрица Г_1 и матрица Г_2 то мы делаем вывод, что изоморфная подматрица найдена и завершаем программу. Но почему мы сделали такой вывод? Для этого мы и выбрали представление графа в виде матрицы инцидентности, так как изоморфный граф можно получить путем перестановки строк и столбцов, то есть любая перестановка ведет к созданию изоморфного графа. Ну а так как мы сравнивали две матрицы и они совпали, значит путем перестановок был получен изоморфный граф. Проиллюстрируем работу программы на следующих страницах (на каждой итерации перебора будет выводиться подматрица с измененными строками и столбцами, а в конце будет выведен изоморфный граф). 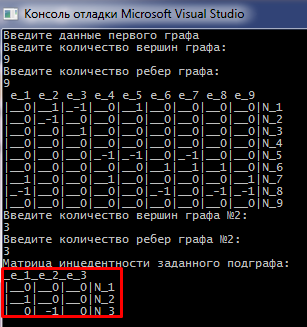 Рисунок 1.Заданные графы 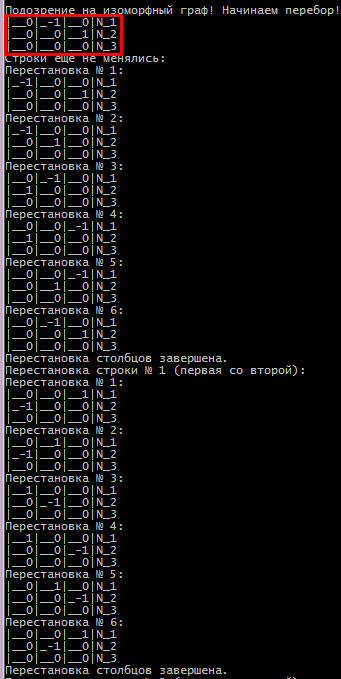 Рисунок 2. Начало перестановок подматрицы, которая может быть изоморфным графом 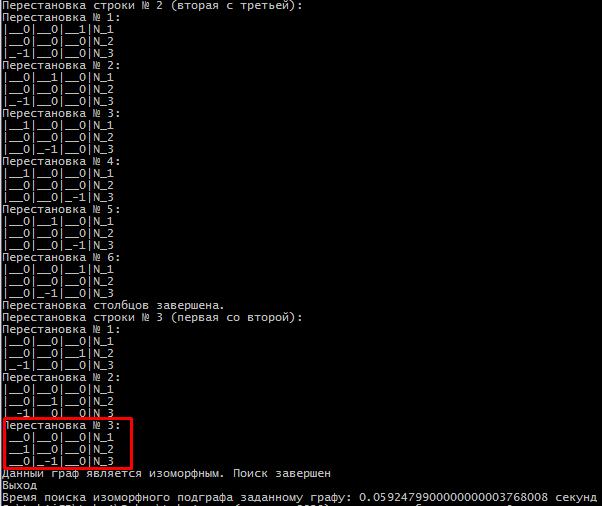 Рисунок 3. Окончание работы алгоритма и вывод времени поиска Как мы видим из работы программы на рисунке 3 выделенная матрица равна матрице выделенной матрице на рисунке 1. Матрицу на рисунке 3 мы получили путем перестановки строк и столбцов на 21 итерации. Следовательно граф, матрица которого выделена на рисунке 2 является изоморфным. Программа отработала корректно. Выводы По итогам выполненной курсовой работы я освоил работу с графов, а именно поиск изоморфного подграфа, представление графа в виде матрицы инцидентности. Также можно сказать, что при очень больших матрицах а именно 6х6 и более время поиска будет возрастать экспоненциально и зависеть от размера матрицы. Поэтому при поиске изоморфного подграфа целесообразно выставлять предельное время поиска, после которого делается вывод, что изоморфного графа не существует. Список используемой литературы: Новиков Ф.А. Дискретная математика: учеб. Для вузов 2-е изд. https://prog-cpp.ru/data-graph/ https://habr.com/ru/post/491846/ Приложение А. Код программы: #include #include #include #include #include using namespace std; int main() { int count_1 = 0; int count_0 = 0; int count_11 = 0; SetConsoleCP(1251); SetConsoleOutputCP(1251); srand(time(NULL)); short number_edge_temp; short number_node_temp; short number_edge_temp_2; short number_node_temp_2; int temp_1 = 0; int temp_2 = 0; int temp_transponirovanie; cout << "Введите данные первого графа\n"; cout << "Введите количество вершин графа: \n"; cin >> number_node_temp; cout << "Введите количество ребер графа: \n"; cin >> number_edge_temp; //выделение памяти для основного графа short** massive_temp = new short* [number_edge_temp]; for (int i = 0; i < number_edge_temp; i++) { massive_temp[i] = new short[number_node_temp]; } //конец выделения памяти для основного графа //заполняем основной граф нулями for (int i = 0; i < number_edge_temp; i++) { for (int j = 0; j < number_node_temp; j++) { massive_temp[i][j] = 0; } } //завершили заполнение графа нулями //формируем матрицу инцедентности основного графа //одно ребро может принадлежать только двум вершинам for (int i = 0; i < number_edge_temp; i++) { while (temp_1 == temp_2) { temp_1 = rand() % (number_node_temp - 1); temp_2 = rand() % (number_node_temp - 1); } massive_temp[i][temp_1] = -1; massive_temp[i][temp_2] = 1; temp_1 = temp_2 = 0; } //закончили формировать матрицу инцедентности основного графа //меняем ориентацию матрицы графа, т.е. стобцы становятся строками, //а строки столбцами short** massive = new short* [number_node_temp]; for (int i = 0; i < number_node_temp; i++) { massive[i] = new short[number_edge_temp]; } for (int i = 0; i < number_edge_temp; i++) { for (int j = 0; j < number_node_temp; j++) { massive[j][i] = massive_temp[i][j]; } } //закончили формирование матрицы инцедентности основного графа //Выводим таблицу инцедентности основного графа for (int i = 0; i < number_edge_temp; i++) { cout << setw(3) << "e_" << i + 1; } cout << "\n"; for (int i = 0; i < number_node_temp; i++) { for (int j = 0; j < number_edge_temp; j++) { cout << "|"; cout << setfill('_'); cout << setw(3) << massive[i][j]; } cout << setw(3) << "|N_" << i + 1 << "\n"; } //конец вывода матрицы инцедентности основного графа cout << "Введите количество вершин графа №2: \n"; cin >> number_node_temp_2; cout << "Введите количество ребер графа №2: \n"; cin >> number_edge_temp_2; //выделение памяти для заданого подграфа short** massive_temp_2 = new short* [number_edge_temp_2]; for (int i = 0; i < number_edge_temp_2; i++) { massive_temp_2[i] = new short[number_node_temp_2]; } //завершили заполнение графа нулями //формируем матрицу инцедентности подграфа //одно ребро может принадлежать только двум вершинам for (int i = 0; i < number_edge_temp_2; i++) { for (int j = 0; j < number_node_temp_2; j++) { massive_temp_2[i][j] = 0; } } massive_temp_2[0][1] = 1; massive_temp_2[1][2] = -1; /*for (int i = 0; i < number_edge_temp_2; i++) { while (temp_1 == temp_2) { temp_1 = rand() % number_edge_temp_2; temp_2 = rand() % number_edge_temp_2; } massive_temp_2[i][temp_1] = -1; massive_temp_2[i][temp_2] = 1; temp_1 = temp_2 = 0; }*/ //закончили формировать матрицу инцедентности заданого подграфа //меняем ориентацию матрицы графа, т.е. стобцы становятся строками, //а строки столбцами short** massive_2 = new short* [number_node_temp_2]; for (int i = 0; i < number_node_temp_2; i++) { massive_2[i] = new short[number_edge_temp_2]; } for (int i = 0; i < number_edge_temp_2; i++) { for (int j = 0; j < number_node_temp_2; j++) { massive_2[j][i] = massive_temp_2[i][j]; } } //выводим матрицу инцедентности заданого подграфа cout << "Матрица инцедентности заданного подграфа:\n"; for (int i = 0; i < number_edge_temp_2; i++) { cout << setw(3) << "e_" << i + 1; } cout << "\n"; for (int i = 0; i < number_node_temp_2; i++) { for (int j = 0; j < number_edge_temp_2; j++) { cout << "|"; cout << setfill('_'); cout << setw(3) << massive_2[i][j]; } cout << setw(3) << "|N_" << i + 1 << "\n"; } cout << "\n"; //Закончили вывод матрицу инцедентности заданого подграфа short* t_col = new short[number_node_temp]; //Начинаем поиск изоморфного подграфа short** massive_temp_3 = new short* [number_edge_temp_2]; for (int i = 0; i < number_edge_temp_2; i++) { massive_temp_3[i] = new short[number_node_temp_2]; } int count_str = 0; int count_col = 0; //cout << "Выводим подматрицы основного графа и сравниваем их с заданной матрицей графа: \n"; Poisk_grafa: //разбиваем матрицу инцедентности основого графа на подматрицы //которые равны матрице подграфа auto start = chrono::steady_clock::now(); for (int i = 0; i < number_node_temp_2; i++) { for (int j = 0; j < number_edge_temp_2; j++) { massive_temp_3[i][j] = massive[i + count_str][j + count_col]; } } //cout << "Подматрица матрицы инцедентности основного графа:\n"; /*for (int i = 0; i < number_node_temp_2; i++) { for (int j = 0; j < number_edge_temp_2; j++) { cout << "|"; cout << setfill('_'); cout << setw(3) << massive_temp_3[i][j]; } cout << setw(3) << "|N_" << i + 1 << "\n"; } cout << "\n";*/ if (count_col == number_edge_temp - number_edge_temp_2) { count_col = 0; count_str++; goto Poisk_grafa; } count_col++; if (count_col == number_edge_temp - number_edge_temp_2 && count_str == number_node_temp - number_node_temp_2) { for (int i = 0; i < number_node_temp_2; i++) { for (int j = 0; j < number_edge_temp_2; j++) { massive_temp_3[i][j] = massive[count_str + i][j + count_col]; } } /*for (int i = 0; i < number_node_temp_2; i++) { for (int j = 0; j < number_edge_temp_2; j++) { cout << "|"; cout << setfill('_'); cout << setw(3) << massive_temp_3[i][j]; } cout << setw(3) << "|N_" << i + 1 << "\n"; }*/ cout << "\n"; |