Курсовая СиАОД. Отчет по курсовой работе по дисциплине структуры и алгоритмы обработки данных на тему "Структуры и алгоритмы обработки данных"

• Название: Отчет по курсовой работе по дисциплине структуры и алгоритмы обработки данных на тему "Структуры и алгоритмы обработки данных"
• Анкор: Курсовая СиАОД
• Дата: 27.01.2023
• Размер: 32.79 Kb.
• Имя файла: Курсовая СиАОД.docx
• Тип: Отчет; #908407

Министерство образования Российской Федерации

Санкт-Петербургский Государственный Электротехнический

Университет «ЛЭТИ»

имени В. И. Ульянова - Ленина

________________________________________________________________________________

КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ


Отчет

по курсовой работе по дисциплине структуры и алгоритмы обработки данных на тему

“Структуры и алгоритмы обработки данных”

Выполнил: Голубков А.М.

Факультет КТИ

Группа 9307

Проверил: Колинько П. Г.

Санкт-Петербург

2010

Содержание:

Часть 1. Множества

1. 
   Цель работы…………………………………………………………………………………………………………….3
   
2. 
   Задание……………………………………………………………………………………………………………………3
   
3. 
   Содержание работы……………………………………………………………………………………………….3
   
4. 
   Контрольные примеры…………………………………………………………………………………………..3
   
5. 
   Результаты исследования алгоритмов…………………………………………………………………..4
   

Часть 2. Деревья

2.1 Цель работы…………………………………………………………………………………………………………….4

2.2 Задание……………………………………………………………………………………………………………………4

2.3 Содержание работы……………………………………………………………………………………………….4

2.4 Использованные структуры……………………………………………………………………………………4

2.5 Оценка сложности алгоритма………………………………………………………………………………..5

2.6 Контрольные примеры…………………………………………………………………………………………..5
Часть 3. Графы общего вида и нагруженные графы
3.1 Цель работы…………………………………………………………………………………………………………….5

3.2 Задание……………………………………………………………………………………………………………………5

3.3 Содержание работы……………………………………………………………………………………………….5

3.4 Выбранный метод хранения данных…………………………………………………………………….5

3.5 Контрольные примеры…………………………………………………………………………………………..6

Часть 1. Множества

1. 
   Цель работы: Приобретение практических навыков работы со множествами при различных способах их представления в программах, а также получение сравнительных оценок эффективности различных способов представления множеств.
   

2. 
   Задание:
   

Реализовать и исследовать четыре способа представления множеств в памяти ЭВМ в программе, которая по заданным множествам A, B, C, D десятичных цифр вычисляет множество, содержащее цифры, общие для множеств A и B, а также все цифры из множества C и из множества D. Измерить время решения задачи для каждого из способов представления множеств.

3. 
   Содержание работы:
   

1. 
   Определить, какие операции над множествами требуется реализовать по индивидуальному заданию. Предложить контрольные примеры.
   
2. 
   Реализовать в виде программы ввод данных заданного класса и формирование из них множеств, выполнение заданных операций над множествами и вывод результата с использованием самого простого (для Вас) способа представления множеств. Добиться прохождения контрольных примеров. Предъявить работающую программу преподавателю.
   
3. 
   Создать, протестировать и отладить варианты программы с другими способами представления множеств. Должны быть рассмотрены следующие способы:
   
   • 
     массив элементов;
     
   • 
     список элементов;
     
   • 
     массив битов;
     
   • 
     двоичные слова;
     
4. 
   Заменить в каждом из вариантов программы ввод исходных данных генерацией множеств. Произвести измерение времени выполнения заданных операций над множествами для каждого из реализованных способов их представления. Определить, в каких случаях время зависит от мощности обрабатываемых множеств.
   

Указание: для измерения времени можно использовать функцию clock() или организовать подсчёт шагов алгоритма обработки множеств. Можно применить оба способа и сравнить результаты.

5. 
   Дать оценку (асимптотическую) размеров памяти, занимаемой множествами в каждом из вариантов программы (ёмкостная сложность).
   

4. 
   Контрольные примеры:
   

Пример 1:

A = {9, 7, 5}

B = {9}

C = {2, 5}

D = {0, 1}

Результирующее множество: E = {9, 2, 5, 0, 1}

Пример 2:

A = { }

B = {1}

C = {5, 4}

D = {3, 9}

Результирующее множество: E = {5, 4, 3, 9}

5. 
   Результаты исследования алгоритмов:
   

Таблица 1. Результаты исследования плгоритмов

Способ представления множеств	Временная сложность	Ёмкостная сложность	Временная сложность (по тексту программы)	Результаты измерения (в таймингах)	Зависимость времени от мощности множества
Массив элементов	O( )	O(1)	O( )	139	Есть
Список элементов	O( )	O(n)	O( )	200	Есть
Массив битов	O(1)	O(1)	O(1)	186	Нет
Двоичные слова	O(1)	O(1)	O(1)	16	Нет

Часть 2. Деревья

2.1 Цель работы: Приобретение опыта составления и отладки программ с рекурсивными функциями.

2.2 Задание:

Составить программу для создания троичного дерева с внутренней (симметричной) нумерацией вершин и подсчёта в нём количества вершин, имеющих не более двух потомков, обходом "в ширину". Программа должна выводить изображение дерева с пронумерованными вершинами на экран и показывать порядок обхода вершин. Оценить теоретическую временную сложность программной реализации алгоритмов обхода дерева.
2.3 Содержание работы: Составить программу по предложенному заданию. Предусмотреть в ней вывод на экран изображения дерева с вершинами, пронумерованными предусмотренным в задании способом и выдачу последовательности номеров вершин в процессе обхода дерева. Дать теоретическую оценку временной сложности алгоритма обхода дерева.
2.4 Использованные структуры:

В данной программе для хранения узла дерева была использована следующая структура:

struct Nd {

int d;

Nd *left;

Nd *right;

Nd *center;

};

Структура состоит из четырёх полей: номер узла и три указателя на левого, правого и центрального сыновей.
2.5 Оценка сложности алгоритма:

Теоретическая сложность алгоритма обхода дерева в ширину составляет O(n).

Сложность алгоритма обхода дерева по тексту программы составляет O(n), т.к. для каждого узла дерева функция будет вызвана один раз.
2.6 Контрольные примеры:

Пример 1:
О
1

4

2

3

6

5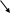
бход дерева в ширину: 1 2 3 4 5 6

Количество узлов, имеющих не более двух потомков: 5

Часть 3. Графы общего вида и нагруженные графы

3.1 Цель работы: Приобретение опыта работы со сложными структурами данных.

3.2 Задание: Реализовать в виде программы и исследовать алгоритм проверки ацикличности графа.

3.3 Содержание работы: Разработать и реализовать в виде программы алгоритм по предложенному заданию. Дать теоретическую оценку временной сложности алгоритма и сравнить её с оценкой по тексту программы. Учесть оценки сложности подалгоритмов ввода исходных данных и вывода результата.

3.4 Выбранный метод хранения данных: При выполнении задания для хранения информации об ориентированном графе был выбран метод задания матрицы смежности.

3.5 Контрольные примеры:

Пример 1.
Т
a

b

c
аблица 3.1 Матрица смежности к Примеру 1.

0	1	1
0	0	1
0	0	0

Т аблица3.2 Матрица достижимости к Примеру 1.

0	1	1
0	0	1
0	0	0

Результат: граф ацикличен.
Пример 2.

Т
a

b

c
аблица 3.3 Матрица смежности к Примеру 2.

0	1	0
0	0	1
1	0	0

Таблица3.4 Матрица достижимости к Примеру 2.

1	1	1
1	1	1
1	1	1

Результат: у графа есть цикл.