Ответы дискретная математика. 1. Что называется объединением, пересечением, разностью, симметрической разностью множеств, дополнением множества

• Название: 1. Что называется объединением, пересечением, разностью, симметрической разностью множеств, дополнением множества
• Анкор: Ответы дискретная математика.docx
• Дата: 20.10.2017
• Размер: 98.39 Kb.
• Имя файла: Ответы дискретная математика.docx
• Тип: Документы; #9579

Часть 1.

1. Что называется объединением, пересечением, разностью, симметрической разностью множеств, дополнением множества?

2. Что такое инъективное, сюръективное, биективное отображение? (с примерами)

Что вы знаете о мощности множеств двоичных наборов и о мощности множества всех подмножеств данного множества?

4. Что такое правило произведения? (с примером)

5. Что такое перестановки и что вы знаете о числе перестановок? (с примерами)

6. Что такое размещение и что вы знаете о числе размещений? (с примером)

7. Что такое сочетания и что вы знаете о числе сочетаний? (с примером)

8. Что такое перестановки и что вы знаете об их числе? {с примером)

9. Что такое рефлексивное, симметричное, транзитивное отношение, отношение эквивалентности и каково его основное свойство?

МО.

11. Что такое отношение строгого порядка, нестрогого порядка?

12. В чем состоит числовое сравнение двоичных наборов и как сравнить двоичные наборы по Парето?
1.

• 
  Объединение - такое мн-во, элементами которого явл все элементы множества А и В
  
• 
  Пересечение - такое мн-во, элементы которого одновременно * входят в А и в В
  
• 
  Разность А и В - такое мн-во, элементы которого принадлежат А, но не принадлежат В
  
• 
  Симметрическая разность - такое мн-во, в которое входят только
  

элементы мн-ва А и только элементы мн-ва B

• 
  Дополнение мн-ва - разность универсального и заданного мн-ва
  

2.

Отображение называют инъективным, если различные элементы мн-ва А переходят в различные элементы мн-ва В.

• 
  Отображение называют сюръективным. если каждый элемент мн-ва В имеет свой прообраз в мн-ве А.
  
• 
  Отображение биективно, когда оно инъективно и сюръективно.
  

3.

Мн-во всех двоичных наборов длины п обозначается Bin. Для любого n - card = .

Мн-во всех подмн-в данного мн-ва А обозначается

card =
4.

Декартовым произведением мн-в А и В называется мн-во всех пар (а, Ь), где а прин А, b прин В. обозн АхВ.


5.

Перестановка - упорядоченный набор чисел (1,2,...,п), обычно трактуемый как биекция на множестве {1,2,п}, которая числу i ставит в соответствие i-й элемент из набора, п различных предметов можно переставить п! различными

способами. Рп = п!
6.

Пусть имеется п различных предметов, из которых нужно выбрать клетук, причем порядок выбора существенен.

= способов

размещения.
7.

Пусть из n различных предметов нужно выбрать к штук, но

порядок выбора НЕ существенен.
способов сочетания
8.

Иногда среди переставляемых предметов есть одинаковые. Пусть имеется kl одинаковых предметов 1-го типа, к2 предметов 2-го типа ... предметов m-готипа, а всего n=kl+k2+...+ предметов.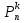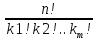

=

9.

Всякое подмн-во Г декартова произведения АхА называется отношением на мн-ве А.

т.е. Г -это мн-во некоторых пар, находящихся в данном отношении, обозн аГЬ

• 
  Отношение называется рефлексивным, если аГа для всех а прин А. т.е. каждый элемент находится в этом отношении сам с собой
  
• 
  Отнош называется антирефлексивным. если аГа никогда не выполняется.
  
• 
  Отнош называется симметричным, если аГЬ => ЬГа (для всех)
  
• 
  Отнош называется антисимметричным, если аГЬ и ЬГа одновременно невозможно.
  
• 
  Отнош называется асимметричным, если аГЬ, ЬГа => а=Ь
  
• 
  Отнош называется транзитивным, если аГЬ, ЬГс => аГс
  
• 
  Если отношение рефлексивно, симметрично и транзитивно, то оно наз. отношением эквивалентности.
  

Основное св-во: Если на мн-ве А задано отношение эквивалентности, то мн-во распадается на объединение непересекающихся классов эквивалентности, в каждом из которых все элементы эквивалентны друг другу.

10.

Отнош Г называется отношением строгого порядка, если оно антирефлексивно, антисимметрично и транзитивно.

Отнош Г называется отношением НЕстрогого порядка, если оно рефлексивно, асимметрично и транзитивно.
11.

Числовое сравнение двоичных наборов заключается в сравнении по первому биту

1000₂ > 0111₂

Очевидно, с таким отношением это мн-во линейно (вполне) упорядочено, т.е. любые наборы можем сравнить как числа.
Сравнение по Парето - сравнение по всем битам

Часть 2.
12.Что такое орграф, граф, вершина, дуга, ребро, путь, цепь, контур, цикл?

13.Каков алгоритм решения задачи о кратчайшем пути в невзвешенном графе?

14.Во взвешенном?

15.Что такое «Эйлерова Цепь» (цикл) У каких графов существуют?

16.Формула Эйлера. Для каких объектов она верна?

17.Как выглядят непланарные графы №1 и №2,1 и 2 типа, и в чем состоит теорема Куратовского-Понтрягина?

18.Что такое хроматическое число графов? Что вы знаете о его величине?

19.Что такое хроматическая величина?


Ответы
12.

орграф - мультиграф, ребрам которого присвоено направление '

Граф - совокупность непустого множества вершин и узлов Вершина - точка, где сходятся и выходят дуги и ребра

Дуга - ориентированное ребро

Ребро - связующая двух вершин в графе

Путь - последовательность ребер или дуг, где конец одного (одной-) служит началом другого (другой), (кроме последней)

Цепь-это путь в неорграфе

Контур - замкнутый путь в орграфе

Цикл- замкнутая цепь в графе
13.

Алгоритм для не взвешенного графа

1)Вершине А присвоим индекс О

2)Всем вершинам, смежным с А, присвоим индекс 1

3)Всем вершинам, смежным с 1, присвоим индекс 2.

Процесс останавливается, когда вершина В получит некоторый индекс n(n - длина кратчайшего пути)

4)Построим этот путь, возвращаясь из вершины В в вершину А

5)Среди вершин, смежных с В, обязательно найдется вершина С с индексом (n-1)

Возвращаемся в С и продолжаем процесс. Ровно через п шагов мы придем в вершину индекса 0, т.е. в вершину А.
Алгоритм для взвешенного графа

1)Вершине А присвоим индекс 0, а всем остальным +°°

2)Будем последовательно перебирать все пары смежным вершин «х» и «у». Каждый раз проверяем неравенство

Если оно выполняется, то уменьшаем индекс индекс , заменив его на 3)Процесс останавливается, когда ни один из индексов нельзя уменьшить. Построим путь с этой суммой, возвращаясь из В в А. Среди всех смежных с В вершин, есть С, где
4)Возвращаемся в С, повторяем процесс, а через некоторое время придем в вершину с индексом 0 (вершина А).
15.

Эйлерова цепь графа - цепь, которая содержитвсе ребра по одному разу.

Эйлеров цикл графа — цикл графа, проходящий через каждое ребро графа ровно по одному разу.
Связный граф обладает незамкнутой эйлеровой цепью <=> две его вершины имеют нечетную степень.

Связный граф обладает незамкнутым эйлеровым циклом О все его вершины имеют четную степень.

16.

Формула Эйлера

В+Г-Р=2 Выполняется для плоского связного графа, где В - вершина, Г - грань, Р - ребро. Также подходит для многогранников в пространстве (при отображении теряется растянутая грань и получается бесконечная грань)
В+Г-Р=К+1<- Если граф плоский, но не связный. Где К - число связных компонентов, К+1 — Эйлерова характеристика графов.

Часть 3
20. Что такое матрица смежности орграфа? каким св-вом обладает матрица смежности неорграфа?

21. Как строится код Харари?

22. Что называется деревом, ордеревом, и как они связаны между собой?

23. Как строится префиксный код бинарного ордерева?

24. Как строится код Прюфера?

25. Какие 3 способа обхода бинарного дерева вы знаете? (с примером >= 10 верш)

26.Что называется атомом ,списком и как связаны деревья со списком?

27. Как связаны число вершин? (с примером)

20.

Пусть дан орграф с п пронумерованными вершинами. Матрица А, размером пхп, заполенная числами: 1, если сущ дуга из i-й вершины в j- ю; 0- если нет, называется матрицей смежности.

Для неорграфа матр смежности симметрична относительно главной диагонали
21.

код Харари:

1)произвольно нумеруем вершины, состаляем треугольник матр смежности

2)располагаем его в виде двоичной строки

3)меняем нумерацию вершин другими двоич числами, наибольшее - код Харари, а соответствующая ему нумерация - каноническая.
22.

Дерево - связный граф, не имеющий циклов.

Ордерево - оргаф, у которого сущетвует вершина х₀ такая, что

• 
  в х₀ не заходит ни одна дуга
  
• 
  в остальные – единственная
  
• 
  не имеет контуров
  

Если в ордереве превратить дуги в ребра, (убрать стрелки), то получим дерево

23.

Префиксный кол бинарного ордерева

Нумеруем все вершины кроме корня, левому корню О, правому -1, потом левому, исходящему от левого 00, правому-01, и наоборот(исходящим от правого -10 и 11). В итоге {00,01,10,11} - префиксный код (считаются все висячие вершины слева направо)
24.код ПрюФера

Пусть дано дерево с п пронумерованными вершинами. Список вершин: 1,2,3,..п

Слева направо ищем первую висячую вершину (al). Ее удаляем из списка и из дерева, а единственную смежную с ней вершину (Ы) заносим в новый список, будущий список Прюфера. Этот процесс повторяем (п-2) раза. В конце получаем список {Ы, Ь2,.. Ь(п-2)}

25.

Способы обхода бинарного ордерева

1)прямой (корень, левое, затем правое поддерево, КЛП)

2)обратный (левое поддерево, корень, правое, ЛКП)

3)концевой (левое поддерево, правое, затем корень, ЛПК)
26.

Атом - буквы, образующие последовательность(любой неделимый объект)

Список - последовательность атомов, элементов и списков, разделяемая запятой и заключенная в общие скобки.

Каждым атомам или спискам соответствует общая безымянная вершина, потомками которой они являются, тогда каждому списку можно будет сопоставить дерево.
27.

Каждому бинарному ордереву можно сопоставить список висячих

вершин. Глубина списка совпадает с глубиной дерева.
Глубина - максимальное число вложенных друг в друга скобок

n= - число вершин через глубину
k= - глубина через число вершин
глубина дерева- число уровней. Совпадает с глубиной списка


17.

Непланарные графы

Теорема Куратовского-Понтрягина

Граф планарен О он не содержит в себе графов первого и второго типов.
18.

Хроматическое число гоаФов - (h) минимальное число цветов, необходимое для правильной раскраски данного графа

1)Полный граф с n врешинами имеет =n

Любое дерево имеет
Почти полное решение дает Теорема Брукса

Если максимальная степень вершины графа d, то <=d+1

(если граф - полный, d=2, и граф содержит цикл нечетной длины)
19.

Хроматическая величина графа - минимальное число цветов, необходимое для правильной раскраски ребер данного графа.