Теория графов БАЛАБА. 9. Гамильтоновы графы. Достаточные условия гамильтоновости графа. 17

• Название: 9. Гамильтоновы графы. Достаточные условия гамильтоновости графа. 17
• Дата: 04.05.2023
• Размер: 1.25 Mb.
• Имя файла: Теория графов БАЛАБА.docx
• Тип: Документы; #1108844
• страница: 1 из 7

1. Основные понятия теории графов. Задачи, послужившие основой теории графов. 2

2. Ориентированные и неориентированные графы. Изоморфизм графов. 4

3. Способы задания графов. Метрические характеристики графа. 6

4. Деревья и леса. 8

5. Плоские графы. Формула Эйлера для плоских графов. 10

6. Основные примеры неплоских графов. Существование у плоского графа вершин малых степеней. 12

7. Теорема Фари. 14

8. Эйлеровы графы. Построение эйлеровых циклов. Обход ребер графа по одному разу в обоих направлениях. 15

9. Гамильтоновы графы. Достаточные условия гамильтоновости графа. 17

10. Взвешенные графы. Минимальное остовное дерево и алгоритмы его построения. 19

11. Кратчайшие пути на графах. Алгоритмы Декстры и Белламана- Мура. 21

12. Кратчайшие пути между всеми парами вершин графа. Алгоритм Флойда. 23

13. Упорядочивание дуг и вершин ориентированного графа. Алгоритм Фалкерсона. 25

14. Алгоритм нахождения максимального пути в графе. 27

15. Потоки в сетях. Построение максимального потока транспортной сети. 29

16. Сетевой график. Правила построения сетевых графиков. 33

17. Двудольные графы. Теорема Кенига. 35

18. Максимальные паросочетания. Количество ребер в максимальном паросочетании. 37

19. Алгоритм построения максимального паросочетания. 39

20. Построение оптимального паросочетания во взвешенном двудольном графе. Задача о назначениях. 40

21. Система различных представителей. Теорема Холла. 41

22. Раскраски графов. Хроматическое число графа. Графы с малым хроматическим числом. 43

23. Алгоритмы построения оптимальных раскрасок. 45

24. Хроматическое число планарного графа. Теорема Хивуда о пяти красках. 47

1. Основные понятия теории графов. Задачи, послужившие основой теории графов.

Граф —  пара двух множеств (V, E), где V={v, … , v_n} – множество вершин, где E={(v_i, v_j)| v_i, v_j  V} – множество ребер, т.е. неупорядоченных пар, если граф неориентированный или упорядоченных пар, если граф ориентированный.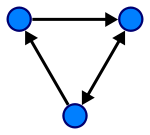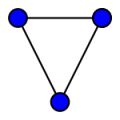



Ориентированный граф Неориентированный граф

Петля - ребро, концы которого совпадают.

Подграф - граф, все вершины и ребра которого содержатся среди вершин и ребер исходного графа.

Смежные вершины – соединены ребром. Если граф ориентированный, то первая вершина – начало ребра, последняя – конец ребра.

Степеньвершины - число выходящих из нее концов ребер. Вершина степени 0 называется изолированной.

Теорема о рукопожатиях – в любом графе сумма степеней всех вершин равна удвоенному числу ребер. В любом графе число вершин нечетной степени – четно.

Простой граф - граф без петель и кратных ребер.

Полный граф – простой граф, в котором каждая пара различных вершин – смежна [K_n].

Связный граф – граф, у которого нет изолированного ребра (точки).

Изоморфные графы – графы, между множеством вершин которых существует взаимно однозначное соответствие, сохраняющее отношение инцидентности (для ориентированных графов сохраняется начало и конец каждого ребра).

Двудольный граф – граф, в котором множество его вершин V можно разбить на два подмножества V₁ и V₂ так, что концы любого ребра принадлежат разным подмножествам.

Цепь – маршрут, у которого все ребра различны.

Простая цепь – цепь, у которого все содержимое кроме крайних различны.

Маршрут – маршрут, содержащий вершины Х₁ и X_n – чередующаяся последовательность х1, u1, x2, u2, … , где х – вершины, u – ребра.

Длина маршрута – количество ребер в нем.

Расстояние между двумя вершинами – длина кратчайшей простой цепи.

В теории графов на систематической основе изучаются их особенности и свойства. Граф представляет собой множество точек и линий, соединяющих эти точки. Родоначальником теории графов является Леонард Эйлер, который решил популярную в те времена задачу о мостах Кёнигсберга.

Одной из первых работ по практическому применению теории графов считается задача с Кёнигсбергскими мостами. В условии заданы река, омываемые рекой острова, и некоторое количество мостов. Требуется дать ответ, есть ли возможность при выходе из заданной точки, перейти каждый из мостов только один раз и возвратиться в исходный пункт.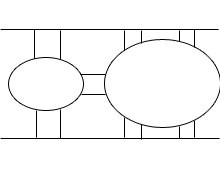



Задача может быть смоделирована так: ко всем участкам на берегу надо прикрепить одну точку, а две точки можно соединить линией лишь в случае, когда участки суши соединяются мостом.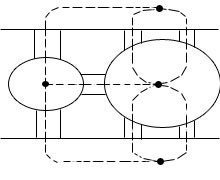



Эйлер сформулировал такой ответ на данную задачу.
Если бы эта задача имела решение, то в сформированном графе должен существовать замкнутый маршрут, который проходит по рёбрам и который сдержит каждое ребро лишь единожды. Если есть такой маршрут, то все вершины должны иметь чётное число рёбер, что в данном случае не выполняется.