Теория графов БАЛАБА. 9. Гамильтоновы графы. Достаточные условия гамильтоновости графа. 17
 Скачать 1.25 Mb.
|
2. Ориентированные и неориентированные графы. Изоморфизм графов.Неориентированные графы – графы, в которых все ребра являются звеньями, то есть порядок двух концов ребра графа не существенен. Ориентированные графы – графы, в которых все ребра являются дугами, то есть порядок двух концов ребра графа существенен. Неориентированный граф можно представить в виде ориентированного графа, если каждое его звено заменить на две дуги с противоположным направлением. Изоморфные графы – графы, между множеством вершин которых существует взаимно однозначное соответствие, сохраняющее отношение инцидентности (для ориентированных графов сохраняется начало и конец каждого ребра). Два графа называются изоморфными, если между множествами их ребер и множествами их вершин установлено взаимно однозначное соответствие, сохраняющее инцидентность, то есть соответствующие ребра соединяют соответствующие вершины. Изоморфные графы можно считать различными представлениями одного и того же графа. Изоморфны ли графы, изображенные на рисунках 4 и 5? Решение. Графы на рисунке 4 изоморфны. Для доказательства этого обозначим соответствующие вершины одинаковыми буквами, см. рис. 6. Нетрудно заметить, что инцидентность соответствующих вершин и ребер сохраняется. Графы на рисунке 5 не изоморфны. Хотя между их вершинами и ребрами можно установить взаимно однозначное соответствие так, чтобы вершины одинаковой степени соответствовали друг другу, но у первого графа вершины степени 2 соединены ребром, а у второго нет.  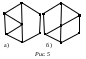 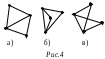 3. Способы задания графов. Метрические характеристики графа.Рассмотрим три способа задания графов: графический, аналитический и матричный. 1) Графический способ. Вершины изображают точками на плоскости, а ребра – линиями, соединяющими соответствующие точки. Для изображения дуги используется линия со стрелкой, указывающей направление от начала к концу дуги. 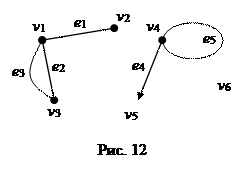 2) Аналитический способ. Граф задают перечислением элементов множества вершин и множества ребер. Для графа, изображенного на рисунке 12, эти множества: V={v1, v2, v3, v4, v5, v6} и Е={e1, e2, e3, e4, e5}, где e1=(v1, v2), e2=(v1, v3), e3=(v1, v3), e4=(v4, v5), и e5=(v4, v4). 3) Матричный способ. Имеется несколько вариантов задать граф матрицей. Наиболее употребимыми являются матрица инциденций и матрица смежности. а) Матрица инциденций – это прямоугольная матрица, число строк которой равно числу вершин, а число столбцов – числу дуг (ребер) графа. Элементы этой матрицы определяются следующим образом: 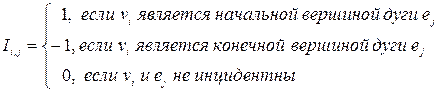 б) Матрица смежности вершин – это квадратная матрица, размер которой определяется числом вершин в графе. Элементы этой матрицы определяются так: 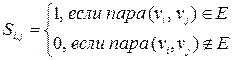 . Если в графе имеются параллельные ребра, то соответствующий элемент матрицы смежности полагают равным числу этих ребер. Метрическими (или числовыми) характеристиками называют параметры графа, определяемые через кратчайшие расстояния между вершинами: центр, радиус и диаметр. Диаметр определяется как самое длинное из всех кратчайших расстояний между вершинами графа, центр - как вершина, максимальное расстояние от которой до всех остальных вершин графа минимально, а это максимальное расстояние от центра есть радиус графа. |