Теория графов БАЛАБА. 9. Гамильтоновы графы. Достаточные условия гамильтоновости графа. 17
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
11. Кратчайшие пути на графах. Алгоритмы Декстры и Белламана- Мура.Зада́ча о кратча́йшем пути́ — задача поиска самого короткого пути (цепи) между двумя точками (вершинами) на графе, в которой минимизируется сумма весов рёбер, составляющих путь. Алгори́тм Де́йкстры — алгоритм на графах, находит кратчайшие пути от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса.  Алгоритм Беллмана —Мура — алгоритм поиска кратчайшего пути во взвешенном графе. За время {\displaystyle O(|V|\cdot |E|)} алгоритм находит кратчайшие пути от одной вершины графа до всех остальных. В отличие от алгоритма Дейкстры, алгоритм Беллмана — Форда допускает рёбра с отрицательным весом.  12. Кратчайшие пути между всеми парами вершин графа. Алгоритм Флойда.Зада́ча о кратча́йшем пути́ — задача поиска самого короткого пути (цепи) между двумя точками (вершинами) на графе, в которой минимизируется сумма весов рёбер, составляющих путь. Метод Флойда непосредственно основывается на том факте, что в графе с положительными весами ребер всякий неэлементарный (содержащий более 1 ребра) кратчайший путь состоит из других кратчайших путей. Этот алгоритм более общий по сравнению с алгоритмом Дейкстры, так как он находит кратчайшие пути между любыми двумя вершинами графа. В алгоритме Флойда используется матрица A размером nxn, в которой вычисляются длины кратчайших путей. Элемент A[i,j] равен расстоянию от вершины i к вершине j, которое имеет конечное значение, если существует ребро (i,j), и равен бесконечности в противном случае. Алгоритм Флойда Основная идея алгоритма. Пусть есть три вершины i, j, k и заданы расстояния между ними. Если выполняется неравенство A[i,k]+A[k,j] Шаг 0. Определяем начальную матрицу расстояния A0 и матрицу последовательности вершин S0. Каждый диагональный элемент обеих матриц равен 0, таким образом, показывая, что эти элементы в вычислениях не участвуют. Полагаем k = 1. Основной шаг k. Задаем строку k и столбец k как ведущую строку и ведущий столбец. Рассматриваем возможность применения замены описанной выше, ко всем элементам A[i,j] матрицы Ak-1. Если выполняется неравенство создаем матрицу Ak путем замены в матрице Ak-1 элемента A[i,j] на сумму A[i,k]+A[k,j] ; создаем матрицу Sk путем замены в матрице Sk-1 элемента S[i,j] на k. Полагаем k = k + 1 и повторяем шаг k. Таким образом, алгоритм Флойда делает n итераций, после i -й итерации матрица А будет содержать длины кратчайших путей между любыми двумя парами вершин при условии, что эти пути проходят через вершины от первой до i -й. На каждой итерации перебираются все пары вершин и путь между ними сокращается при помощи i -й вершины. 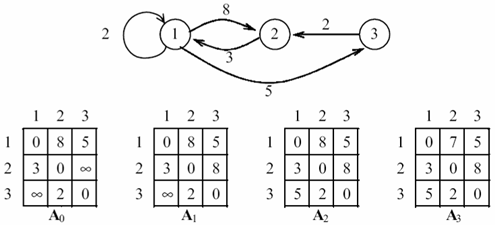 13. Упорядочивание дуг и вершин ориентированного графа. Алгоритм Фалкерсона.Под упорядочиванием вершин связного орграфа без циклов понимают такое разбиение его вершин на группы, при котором: 1) вершины первой группы не имеют предшествующих вершин, а вершины последней группы последующих; 2) вершины любой другой группы не имеют предшествующих в следующей группе; 3) вершины одной и той же группы дугами не соединяются. Аналогичным образом вводится понятие упорядочения дуг. В результате упорядочения элементов получают орграф, изоморфный исходному. Упорядочение элементов выполняется графическим или матричным способом. Графический способ упорядочивание вершин, дуг орграфа носит название алгоритма Фалкерсона. Алгоритм Фалкерсона (движение вперед) для упорядочения вершин: 1. Находят вершины графа, в которые не входит ни одна дуга. Они образуют первую группу. Нумеруют вершины группы в натуральном порядке 1, 2, ... . При этом присвоение номеров вершинам внутри группы может быть сделано не единственным образом, что не имеет значения. 2. Мысленно вычеркиваем все пронумерованные вершины и дуги, из них выходящие. В получившемся графе найдется, по крайней мере, одна вершина, в которую не входит ни одна дуга. Этой вершине, входящей во вторую группу, присваивается очередной номер и т.д. Этот шаг повторяется до тех пор, пока все вершины не будут упорядочены (пронумерованы). Алгоритм Фалкерсона для упорядочения дуг: 1. Найти дуги, не имеющие непосредственно предшествующих (они образуют I группу). 2. Вычеркнуть найденные дуги; после этого появится, по крайней мере, одна новая дуга, не имеющая непосредственно предшествующей (в графе без дуг I группы). Такие дуги составляют II группу. Повторять этот шаг, пока все дуги не будут разбиты на группы. В заключение упорядочения дугам присваивают новые обозначения с индексами 1, 2, ... . Пример. Графическим способом упорядочить вершины и дуги заданного орграфа. Решение. Используя алгоритм Фалкерсона, упорядочим вершины и дуги заданного орграфа.  |
