Теория графов БАЛАБА. 9. Гамильтоновы графы. Достаточные условия гамильтоновости графа. 17
 Скачать 1.25 Mb.
|
7. Теорема Фари.В математике теорема Фари утверждает, что любой простойпланарный граф может быть нарисованный без пересечений с прямыми краями отрезки. То есть возможность рисовать ребра графа как кривые, а не как отрезки прямых линий, не позволяет рисовать больший класс графов. Теорема названа в честь Иштвана Фари , хотя она была независимо доказана Клаусом Вагнером (1936 ), Фари (1948 ) и Шерман К. Стейн (1951 ). Д  ля любого плоского графа существует его плоское представление, у которого все ребра изображаются прямолинейными отрезками.1) Индукции по числу вершин 2) Существует вершина степени <=5. Считаем она внутри вершины контура и удаляем А вместе со всеми прилигающими ребрами. Получается грань 4-х или 5-угольника. Число вершин стало n-1. 3) Показать, что в этом 4-х или 5-ти угольнике существует место для А. Рассматриваются случаи невыпуклых многоугольников. 8. Эйлеровы графы. Построение эйлеровых циклов. Обход ребер графа по одному разу в обоих направлениях.Эйлеров граф отличен тем, что в нем можно обойти все вершины и при этом пройти одно ребро только один раз. В нём каждая вершина должна иметь только чётное число рёбер. Правильным обходом графа, или эйлеровым путем, называется такой маршрут, при котором все ребра графа проходятся ровно по одному разу. Эйлеровым циклом называется эйлеров путь, являющийся циклом. Граф называется эйлеровым, если в нем существует эйлеров цикл.  . Связный граф является эйлеровым тогда и только тогда, когда он четный. С 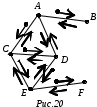 делать полный обход графа на рис.19, пройдя каждое ребро по одному разу в каждом направлении.Р 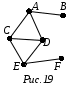 ешение. Начнем обход, например, с вершины А. Будем отмечать пройденный путь стрелками, как описано в алгоритме, см. рис.20. Маршрут будет следующий: A ↦ B * A ↦ C ↦ D A * D ↦* E ↦ F * E * C * E * D * C * A. Стрелка со звездочкой означает, что на соответствующем шаге выбранное продолжение маршрута является единственно возможным. Описанный метод можно применить для прохождения лабиринтов. Коридорам лабиринта соответствуют ребра графа, развилкам и тупикам – вершины. Следует обойти граф, как указано выше, пройдя каждый коридор по два раза: по одному в каждом направлении. Начало и конец каждого коридора следует отмечать стрелками, как указано в алгоритме. Стрелка с точкой ставится в конце коридора, если в соответствующую развилку попали в первый раз. Так как в результате весь лабиринт будет пройден, когда-нибудь будет найден выход. При повторном прохождении лабиринта следует идти только по стрелкам, для которых отсутствуют встречные стрелки. 9. Гамильтоновы графы. Достаточные условия гамильтоновости графа.Гамильтоновым графом называется граф, содержащий гамильтонов цикл. 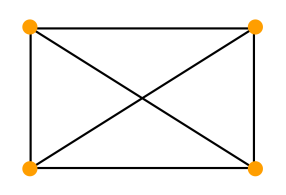 Гамильтоновым циклом называется простой цикл, который проходит через все вершины рассматриваемого графа. Говоря проще, гамильтонов граф — это такой граф, в котором можно обойти все вершины, и каждая вершина при обходе повторяется лишь один раз.  10. Взвешенные графы. Минимальное остовное дерево и алгоритмы его построения.Взвешенным графом называется граф, вершинам и/или ребрам которого присвоены «весы» — обычно некоторые числа. Пример взвешенного графа — транспортная сеть, в которой ребрам присвоены весы: они показывают стоимость перевозки груза по ребру и пропускные способности дуг. 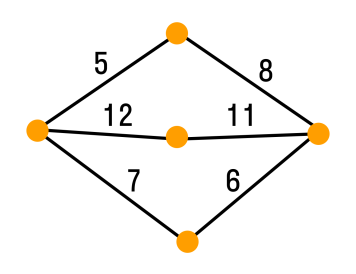 Остовным деревом графа называется его подграф, являющийся деревом и содержащий все вершины графа. На практике ребра графа могут быть снабжены дополнительной числовой характеристикой, называемой весом ребра. Такой граф называется взвешенным. Например, если граф – это сеть дорог, то вес может означать длину дорог, или стоимость перевозки груза, или время движения, и т.д. Обычно решается задача поиска минимального остовного дерева, то есть остовного дерева с минимальным суммарным весом ребер. Упражнение 5.4.1. Докажите, что минимальное остовное дерево существует. Опишем жадный алгоритм для построения минимального остовного дерева. Находим ребро с минимальным весом и включаем его в строящееся остовное дерево. Из оставшихся ребер отбрасываем те, при добавлении которых к уже построенному дереву образуется цикл. Среди оставшихся находим ребро с минимальным весом и включаем его в строящееся остовное дерево. Пункт 2 повторяем, пока не будет построено дерево. Замечание. Если на некотором шаге обнаруживаются несколько ребер с минимальным весом, то берем любое. П  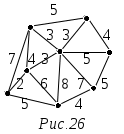 остроить минимальное остовное дерево для графа, изображенного на рис. 26.Шаг 1. Начальной вершине А присваиваем окончательную метку 0, всем остальным вершинам – временные метки +. Шаг 2. Для вершины Ai, метка которой получила на предыдущем шаге окончательное значение ai, определяем все возможные продолжения маршрута. Каждой не имеющей окончательной метки вершине Aj, в которую из ai ведет ребро с весом bij, присваиваем новую временную метку ai +bij, если это число меньше ее старой метки. Шаг 3. Из всех временных меток выбирается наименьшая и объявляется окончательной. В случае равенства меток выбирается любая из них. Шаг 4. Если вершина В получила окончательную метку, алгоритм останавливается. В противном случае возвращаемся к шагу 2. |