Теория графов БАЛАБА. 9. Гамильтоновы графы. Достаточные условия гамильтоновости графа. 17
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
14. Алгоритм нахождения максимального пути в графе.Максимальным путем называется путь с максимальным весом . В общем случае, в одном графе может быть несколько максимальных путей. Построение максимального пути во взвешенном ориентированном графе возможно, если в нем нет контуров с положительным весом. Если в графе есть такой контур, то некоторые пути могут иметь сколь угодно большой вес, т.к. каждый обход контура увеличивает вес пути на величину веса этого контура. Для нахождения максимального пути граф G (сеть) должен быть ациклическим, ибо в противном случае может оказаться, что длины некоторых путей не ограничены сверху. Если Gn - ациклический граф, то для любых двух его вершин xi ? xj выполняется одно из условий: 1. xi предшествует xj, xiSпредш (xj); 2. xi следует за xj, xiSслед (xj); 3. нет пути между xi и xj., Первое и второе условия одновременно не выполнимы из-за требуемой ацикличности графа. Перед вычислением максимального пути в орграфе необходимо упорядочить вершины графа по алгоритму Фалкерсона. Сам алгоритм вычисления максимального пути чисто перечислительный. Он перебирает все возможные пути от текущей вершины до всех последующих, достижимых из текущей вершины. Пусть dj - длина максимального пути от вершины x1 до вершины xj, тогда величина dj удовлетворяет следующим рекуррентным соотношениям (1. 2. 5): 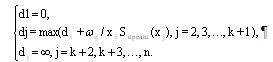 Соотношения (1. 2. 5) позволяют легко вычислить длины максимальных путей от s = x1 до вершин, достижимых из вершины s. Сами пути могут быть построены методом последовательного возвращения (второй этап в алгоритме Дейкстры). 15. Потоки в сетях. Построение максимального потока транспортной сети.Потоком по транспортной сети называется целочисленная функция (u), заданная на множестве ребер и обладающая свойствами: (uU) (u) С(u); для каждой внутренней (отличной от начала и конца) вершины х графа  = =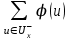 , где , где 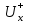 – множество ребер, входящих в вершину х, – множество ребер, входящих в вершину х, 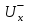 – множество ребер, выходящих из вершины х. – множество ребер, выходящих из вершины х.Смысл функции (u) – это количество транспорта, пропускаемого через сеть. Условие (1) означает, что количество транспорта, пропускаемого по ребру u, не превышает пропускную способность ребра. Условие (2) утверждает, что поток, входящий в вершину, равен выходящему (поток в вершинах не скапливается). Обозначим поток, выходящий из начальной вершины, через (х0), а поток, входящий в конечную вершину, через (z). Очевидно, (х0) = (z). Задача, связанная с транспортной сетью, – максимизировать поток, пропускаемый по сети. На графике каждое ребро транспортной сети помечается дробью, числитель которой означает пропускную способность ребра, а знаменатель – поток, проходящий по этому ребру. Пусть A X – множество вершин транспортной сети, х0А, zA. Разрезом транспортной сети называется множество  ребер, входящих в А. Мощностью разреза называется С(А) = ребер, входящих в А. Мощностью разреза называется С(А) = 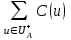 (это максимально возможный поток, входящий в А по ребрам разреза). (это максимально возможный поток, входящий в А по ребрам разреза).5.6.1. (z) С(А). Доказательство. У множества А могут быть выходящие дуги, по которым часть потока, входящего в разрез, выходит из А. Поэтому (z) (А), где (А) – поток, входящий в А по дугам разреза. Но (А) С(А), откуда (z) С(А). 5.6.2 (Форд – Фалкерсон). Максимальный поток по транспортной сети равен минимальной из мощностей разрезов, то есть 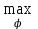 (z) = (z) = 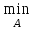 С(А). С(А).Доказательство. Из теоремы 1 имеем 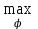 (z) (z) 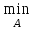 С(А). Чтобы доказать равенство, достаточно построить поток * и найти множество А* такие, что *(z) = С*(А). Тогда из неравенства будет следовать, что поток максимальный, а разрез минимальный. С(А). Чтобы доказать равенство, достаточно построить поток * и найти множество А* такие, что *(z) = С*(А). Тогда из неравенства будет следовать, что поток максимальный, а разрез минимальный.Максимальный поток строим с помощью следующего алгоритма, который состоит из двух частей. 1. Насыщение потока. Поток называется насыщенным, если любой путь из x0 в z содержит ребро u, для которого (u) = С(u) (насыщенное ребро). 1.1. Задаем произвольный начальный поток, например, нулевой на всех ребрах. 1.2. Ищем путь из x0 в z. Если путь найден, то переходим к пункту 1.3. Если путь не существует, то переходим к пункту 1.5. 1.3. Увеличиваем поток по найденному пути так, чтобы одно из ребер стало насыщенным. 1.4. Условно разрываем насыщенное ребро (все, если их несколько) и переходим к пункту 1.2. 1.5. Сеть насыщена и разорвана. 2. Перераспределение потока. Пометим рекурсивным образом все возможные вершины в сети. 2.1. Вершину x0 пометим –0. 2.2. Пусть xi – любая помеченная вершина, y – смежная с ней непомеченная. Вершину у помечаем +i, если данные вершины соединены ненасыщенным ребром xi y, и помечаем –i, если вершины соединены непустым ребром xi y. После пометки вершин возможны два случая: вершина z оказалась либо помеченной, либо непомеченной. 2.3. Вершинаz оказалась помеченной. Значит, существует последовательность помеченных вершин от х0 к z. В этой последовательности каждая последующая вершина помечена номером предыдущей со знаком + или –. Перераспределим поток на соответствующем маршруте, увеличивая его на ребрах, ориентированных по направлению движения от х0 к z, и уменьшая на ребрах, ориентированных в противоположном направлении. Это можно делать до тех пор, пока одно из ребер не станет насыщенным или пустым. При этом суммарный поток по сети увеличится, так как увеличится поток, выходящий из вершины от х0. Далее снова переходим пункту 2.1. 2.4. Вершинаz оказалась непомеченной. Это означает конец работы алгоритма, то есть полученный поток * является максимальным. Действительно, пусть А* – множество всех непомеченных вершин. Тогда ребра, входящие извне в эти вершины, насыщенные, а выходящие – пустые. Множество А* определяет разрез, так как х0А, zA. Так как входящие в А* ребра насыщенные, то *(А*) = С(А*). Так как выходящие из А* ребра пустые, то весь входящий в А* поток скатывается в z, и *(z) = *(А*) = С(А*). Работа алгоритма завершится за конечное число шагов, так как после каждого шага поток увеличивается на целое число, а сверху он ограничен пропускной способностью сети. Это доказывает теорему. |
