Теория графов БАЛАБА. 9. Гамильтоновы графы. Достаточные условия гамильтоновости графа. 17
 Скачать 1.25 Mb.
|
4. Деревья и леса.Деревом называется связный граф без циклов. Любые две вершины дерева соединены лишь одним маршрутом.  Лес-это неориентированный граф, в котором любые две вершины соединены не более чем одним путем. Эквивалентно, лес-это неориентированный ациклический граф, все связные компоненты которого являются деревьями; другими словами, граф состоит из непересекающегося объединения деревьев. Деревом называется связный граф, который не содержит циклов. Таким образом, в дереве невозможно вернуться в исходную вершину, перемещаясь по ребрам и не проходя по одному ребру два или более раз. Циклом называется замкнутый путь, который не проходит дважды через одну и ту же вершину. Простым путем называется путь, в котором никакое ребро не встречается дважды. Легко проверить, что дерево — это граф, в котором любые две вершины соединены ровно одним простым путем. Если выкинуть любое ребро из дерева, то граф станет несвязным. Поэтому: Дерево — минимальный по числу рёбер связный граф. Лес — упорядоченное множество упорядоченных деревьев. Висячей вершиной называется вершина, из которой выходит ровно одно ребро. Определения дерева: Деревом называется связный граф не содержащий простых циклов. Деревом называется связный граф, содержащий n вершин и n - 1 ребро. Деревом называется связный граф, который при удалении любого ребра перестает быть связным. Деревом называется граф, в котором любые две вершины соединены ровно одним простым путем. Очень часто в дереве выделяется одна вершина, которая называется корнем дерева. Дерево с выделенным корнем называют корневым или подвешенным деревом. Пример: генеалогическое дерево. I теорема - В дереве с более чем одной вершиной есть висячая вершина. II теорема - В дереве число вершин на 1 больше числа ребер. III теорема - У любого связного графа есть остовное дерево. 5. Плоские графы. Формула Эйлера для плоских графов.Граф называется плоским, если существует его представление на плоскости, при котором ребра не пересекаются во внутренних точках, то есть плоское представление. В 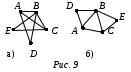 о многих источниках такой граф называется планарным, а плоским графом называют плоское представление планарного графа.Граф на рисунке 9 а) является плоским, так как на рисунке 9 б) приведено его плоское представление. Для связного плоского графа выполняется соотношение Г + В – Р = 2 (формула Эйлера). Доказательство. Пусть дан произвольный плоский граф. Будем удалять у него поочередно по одному ребру, разделяющему две различные грани. На каждом таком шаге уменьшается на 1 число ребер и число граней, так как две грани объединяются в одну. Граф при этом остается связным. Действительно, связность может нарушиться, только если удаляемое ребро входит в границу грани два раза, как на рисунке 10 ребро АВ входит в границу заштрихованной грани. Но в этом случае это ребро не разделяет две различные грани и не подлежит удалению. Продолжаем этот процесс до тех пор, пока не останется одна грань. Это значит, что получим граф без циклов, то есть дерево. Для него, согласно теореме 5.1.2, выполняется соотношение ГД + ВД – РД = 2. А так как у исходного графа по построению В = ВД , а Г – Р =ГД – РД, то отсюда получаем утверждение теоремы. Ф 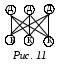 ормула Эйлера обобщается на случай несвязного плоского графа. В этом случае в рассмотрение вводится еще число К связных компонент графа, и формула принимает вид Г + В – Р – К = 1.6. Основные примеры неплоских графов. Существование у плоского графа вершин малых степеней.Плоским графом называется граф, изображенный на плоскости так, что никакие два его ребра (или, вернее, представляющие их кривые) геометрически не пересекаются нигде, кроме инцидентной им обоим вершины. Граф, изоморфный плоскому графу, называется планарным. Планарный граф можно определить еще так: граф планарен, если его можно уложить на плоскости. Рисунок графа, в котором никакие два его ребра не пересекаются, если не считать точками пересечения общие вершины, называют плоским представлением графа. Ясно, что плоское представление имеет только плоский граф. Обратно, у всякого плоского графа непременно найдется плоское представление. Плоские графы — это простые циклы, деревья, лес, а также граф, содержащий цикл, из вершин которого "выходят" деревья. Пример. Примером неплоского графа может служить полный граф с пятью вершинами. Любые попытки начертить его плоское представление обернутся неудачей. В качестве характеристики плоского представления графа вводится понятие грани. Гранью в плоском представлении графа  называ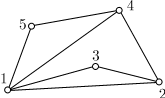ется часть плоскости, ограниченная простым циклом и не содержащая внутри других циклов.Пример.  На рисунке показано плоское представление графа с тремя гранями:  ,  ,  . Часть плоскости, ограниченная простым циклом  , гранью не является, так как содержит цикл . Простой цикл, ограничивающий грань, называется границей грани. Две грани будем называть соседними, если их границы имеют хотя бы одно общее ребро.  |