Теория графов БАЛАБА. 9. Гамильтоновы графы. Достаточные условия гамильтоновости графа. 17

• Название: 9. Гамильтоновы графы. Достаточные условия гамильтоновости графа. 17
• Дата: 04.05.2023
• Размер: 1.25 Mb.
• Имя файла: Теория графов БАЛАБА.docx
• Тип: Документы; #1108844
• страница: 7 из 7

16. Сетевой график. Правила построения сетевых графиков.

Сетевой график представляет собой ориентированный граф, в котором вершины соответствуют событиям, а дуги – работам.

События на сетевом графике (графе) изображаются вершинами графа, а работы – ориентированными дугами, показывающими связь между ними.

У сетевого графика есть начальная (исходная) вершина, не имеющая входящих дуг, и конечная вершина (завершающее событие), не имеющая выходящих дуг.

Существуют некоторые базовые правила составления сетевого графика:

1. 
   каждая работа должна быть заключена между двумя событиями. В сети не может быть работ, имеющих одинаковые коды;
   

2. 
   в сети не должно быть событий, из которых не выходит ни одной работы, если только это событие не является для данного графика завершающим; соответственно, в сети не должно быть события, в которое не входит ни одной работы, если только это событие не является исходным;
   

3. 
   в сетевом графике не должно быть замкнутых контуров.
   

4. 
   Построить сетевой график работы по данным, приведенным на рис.31.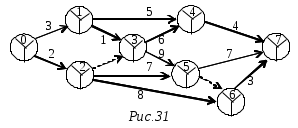
   

Решение. Заполняем сначала левые сектора. Результат приведен на рис.32.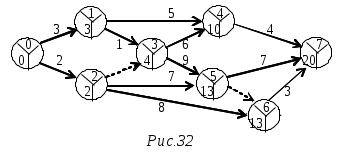



Затем заполняем правые сектора. Определяем цепь, задающую жесткий график работ. Окончательный результат приведен на рис.33.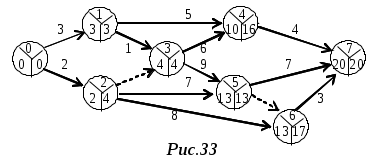

17. Двудольные графы. Теорема Кенига.

Граф называется двудольным, если множество его вершин можно разбить на два подмножества так, чтобы никакое ребро не соединяло вершины одного и того же подмножества.

Двудо́льный граф или бигра́ф -  это граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет вершину из одной части с какой-то вершиной другой части, то есть не существует рёбер между вершинами одной и той же части графа.



Например, полный двудольный граф состоит из двух множеств вершин и из всевозможных звеньев, которые соединяют вершины одного множества с вершинами другого множества.

В теории графов теорема Кёнига (теорема Кёнига-Эгервари, венгерская теорема^[1]), доказанная Денешем Кёнигом в 1931^[2], утверждает эквивалентность задач нахождения наибольшего паросочетания и наименьшего вершинного покрытия в двудольных графах.

18. Максимальные паросочетания. Количество ребер в максимальном паросочетании.

Максимальное паросочетание — это такое паросочетание M в графе G, которое не содержится ни в каком другом паросочетании этого графа, то есть к нему невозможно добавить ни одно ребро, которое бы являлось несмежным ко всем рёбрам паросочетания.

Другими словами, паросочетание M графа G является максимальным, если любое ребро в G имеет непустое пересечение, по крайней мере, с одним ребром из M. Ниже приведены примеры максимальных паросочетаний (красные рёбра) в трёх графах.

Максимальное паросочетание можно найти простым жадным алгоритмом.

Cамым большим максимальным паросочетанием является наибольшее паросочетание, которое может быть найдено за полиномиальное время.

Однако неизвестно никакого полиномиального по времени алгоритма для нахождения наименьшего максимального паросочетания, то есть максимального паросочетания, содержащего наименьшее возможное число рёбер.

Заметим, что наибольшее паросочетание из k рёбер является рёберным доминирующим множеством с k рёбрами. И обратно, если задано минимальное рёберное доминирующее множество с k рёбрами, мы можем построить наибольшее паросочетание с k рёбрами за полиномиальное время.

Таким образом, задача нахождения минимального по размеру максимального паросочетания эквивалентна задаче нахождения минимального рёберного доминирующего множества^[15].



Множество ребер называется независимым (паросочетанием), если никакие два из них не смежны. Наибольшее число ребер, образующих независимое мно-жество, называется реберным числом независимости и обозначается β1.

19. Алгоритм построения максимального паросочетания.

20. Построение оптимального паросочетания во взвешенном двудольном графе. Задача о назначениях.

Подмножество ребер M ⊆ E называется паросочетанием в графе G, если каждой вершине v ∈ V инцидентно не более одного ребра из M.

Паросочетание, покрывающее все вершины графа, называется совершенным.

Вершинным покрытием графа называется такое подмножество вершин R ⊆ V, что каждое ребро графа e ∈ E инцидентно по крайней мере одной вершине из R.

Между паросочетанием и вершинным покрытием графа существует (двойственная) взаимосвязь. А именно, для любых паросочетания M и вершинного покрытия R, имеет место неравенство |M| ≤ |R|.

Действительно, пусть M = {(i1, j1), …, (ik, jk)} паросочетание. Тогда в вершинном покрытии R должна быть хотя бы одна из вершин каждой пары {is, js}, s = 1, …, k. Следовательно, |R| ≥ k = |M|.

21. Система различных представителей. Теорема Холла.

Пусть   - некоторые множества и имеются элементы  ; элементы   называются Системой различных представителей, если все они попарно различны.

Система различных предствавителей соответствует максимальному паросочетанию.



Система множеств   Обладает системой различных представителей тогда и только тогда, когда в объединении любых K Множеств из числа данных   Имеется K различных элементов, 

22. Раскраски графов. Хроматическое число графа. Графы с малым хроматическим числом.

Раскраска графа — теоретико-графовая конструкция, частный случай разметки графа. При раскраске элементам графа ставятся в соответствие метки с учётом определённых ограничений; эти метки традиционно называются «цветами».

В простейшем случае такой способ окраски вершин графа, при котором любым двум смежным вершинам соответствуют разные цвета, называется раскраской вершин.

Аналогично раскраска рёбер присваивает цвет каждому ребру так, чтобы любые два смежных ребра имели разные цвета^[1].

Наконец, раскраска областей планарного графа назначает цвет каждой области, так, что каждые две области, имеющие общую границу, не могут иметь одинаковый цвет.

Раскраска вершин — главная задача раскраски графов, все остальные задачи в этой области могут быть сведены к ней.

Например, раскраска рёбер графа — это раскраска вершин его рёберного графа, а раскраска областей планарного графа — это раскраска вершин его двойственного графа^[1].



Хроматическое число графа – минимальное число красок, которое требуется для правильной раскраски графа.



Хроматический класс графа G — минимальное число цветов, в которые можно раскрасить ребра графа G так, чтобы смежные ребра имели разные цвета. Обозначается χ'(G).

Проблема реберной раскраски произвольного плоского кубического графа без мостов тремя цветами эквивалентна знаменитой Проблеме четырёх красок. Реберная раскраска определяет 1-факторизацию графа.

Рёберная раскраска графа подразумевает под собой назначение цветов ребрам так, что никакие два ребра одного цвета не принадлежат одной вершине. Эта задача эквивалентна разделению множества граней на множества независимых граней.

23. Алгоритмы построения оптимальных раскрасок.

Рёберная раскраска графа подразумевает под собой назначение цветов ребрам так, что никакие два ребра одного цвета не принадлежат одной вершине. Эта задача эквивалентна разделению множества граней на множества независимых граней.

Тотальная раскраска — это один из видов раскраски вершин и рёбер графа. Под ней подразумевают такое присвоение цветов, что ни соседние вершины, ни смежные ребра, ни вершины и ребра, которые их соединяют, не имеют одинакового цвета.



Жадная раскраска рассматривает вершины графа последовательно и присваивает каждой вершине свой первый доступный цвет, т. е. вершины рассматриваются в определенном порядке v₁, v₂, … v_n, а также v_i и назначен наименьший доступный цвет, который не используется ни одним из v_i соседи.

1) Выделим максимальное независимое множество вершин и ставим им в соответствие первый цвет: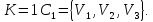



2) Из оставшихся вершин формируем независимое множество и ставим им в соответствие второй цвет: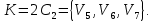



3) Берем третий цвет и, из всех оставшихся вершин, формируем независимое множество: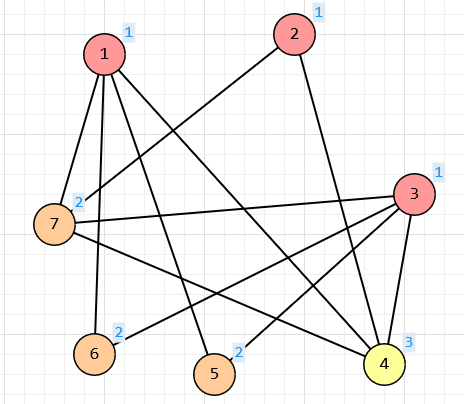





Последовательный алгоритм - последовательно раскрашиваются вершины – берется очередная вершина и раскрашивается в цвет, не совпадающий с цветами смежных окрашенных вершин.

Быстрый алгоритм раскраски с использованием битовых операций - Авторы алгоритма работают с матрицей смежности и полагают, что любая вершина графа соединяется сама с собой, поэтому на главной диагонали матрицы будут стоять единицы. Между двумя вершинами может быть только одно ребро.

24. Хроматическое число планарного графа. Теорема Хивуда о пяти красках.

Хромати́ческое число́ гра́фа G — минимальное число цветов, в которые можно раскрасить^[1] вершины графа G так, чтобы концы любого ребра имели разные цвета. Обычно обозначается χ(G).

Множество всех полиграфических карт с точки зрения теории графов представляет собой множество всех планарных графов

Лемма: В любом планарном графе G существует вершина степени не больше 5.

Теорема о пяти красках — вершины любого планарного графа можно покрасить в пять цветов так, чтобы любые две смежные вершины были разных, или, что то же самое, хроматическое число планарного графа не больше 5.

1) n=1 χ(G)=1<=5

2) Предполагаем, что для всех планарных графов, число вершин меньше n, условие выполнено.

3) В плоском графе существует вершина, степень которой не превосходит <=5. Удалим эту вершину, получим граф с n-1 вершиной.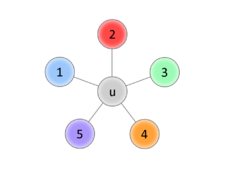



Обозначим за u — возвращаемую вершину, v(k)— вершину, покрашенную в k цвет.
Если среди вершин, смежных u, есть две вершины одного цвета, значит остаётся по меньшей мере один свободный цвет, в который мы и покрасим u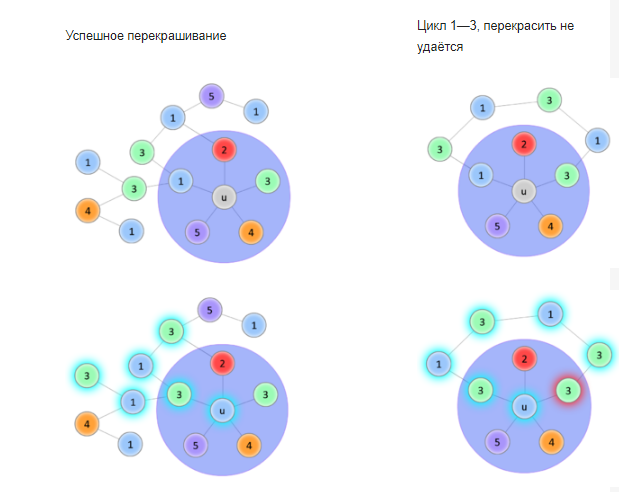

.