Отчет по лабораторнопрактической работе 11
 Скачать 297.41 Kb. Скачать 297.41 Kb.
|
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА – Российский технологический университет» РТУ МИРЭА
Институт кибернетики (ИК) Кафедра общей информатики (ОИ) ОТЧЕТ ПО ЛАБОРАТОРНО-ПРАКТИЧЕСКОЙ РАБОТЕ №11 Синтез четырехразрядного счетчика с параллельным переносом между разрядами двумя способами по дисциплине «ИНФОРМАТИКА»
Москва 2021 СОДЕРЖАНИЕ1Постановка задачи 3 2Проектирование и реализация 4 1.1Восстановленная таблица переходов счетчика 4 Таблица переходов является частично определенной: состояния 1110 и 1111, согласно исходным данным, возникать никогда не должны, поэтому очередное состояние Q(t + 1) для этих случаев мы может интерпретировать как нам удобно в целях минимизации управляющей логики. 4 1.2Проектирование оптимальных схем управления триггерами 4 1.3Реализация счетчика с оптимальной схемой управления 9 1.4Реализация счетчика на преобразователе кодов 10 3Выводы 11 4Информационные источники 12 Постановка задачиРазработать счетчик с параллельным переносом на D-триггерах двумя способами: с оптимальной схемой управления, выполненной на логических элементах общего базиса; со схемой управления, реализованной на преобразователе кодов (быстрая реализация, но не оптимальная схема). В качестве исходных данных использовать индикатор CNT лабораторного комплекса, на котором слева направо отображены: направление счета (0 – сложение, 1 – вычитание); максимальное значение счетчика (не путать с модулем счета); шаг счета. Протестировать работу схемы и убедиться в ее правильности. Подготовить отчет о проделанной работе и защитить ее. Проектирование и реализацияПосле ввода личного кода в программу мы получили индикатор CNT = 1d7. Теперь восстановим по нему таблицу переходов счетчика (см. таблица 1). Таблица 1 – таблица переходов счетчика
Рассмотрим столбцы Qi(t + 1) как самостоятельные функции от четырех переменных и проведем их минимизацию, то есть построим карты Карно для МДНФ и МКНФ каждой функции(рис. 1-8).
 Рисунок 1 – Карта Карно для МДНФ функции Q3(t + 1)
Рисунок 2 – Карта Карно для МКНФ функции Q3(t + 1) Из рис. 1 и рис. 2 видно, что МКНФ описывается меньшим количеством переменных, чем МДНФ, поэтому в целях минимизации возьмем МДНФ. Запишем МКНФ для Q3(t + 1): 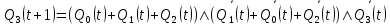 (1) (1)
Рисунок 3 – Карта Карно для МДНФ функции Q2(t + 1)
   Рисунок 4 – Карта Карно для МКНФ функции Q2(t + 1) Из рис. 3 и рис. 4 видно, что МДНФ описывается меньшим количеством переменных, чем МКНФ, поэтому в целях минимизации возьмем МДНФ. Запишем МДНФ для Q2(t + 1): 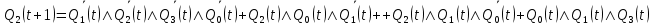 + + 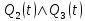 (2) (2)
Рисунок 5 – Карта Карно для МДНФ функции Q1(t + 1)
Рисунок 6 – Карта Карно для МКНФ функции Q1(t + 1) Из рис. 5 и рис. 6 видно, что МДНФ описывается меньшим количеством переменных, чем МКНФ, поэтому в целях минимизации возьмем МДНФ. Запишем МДНФ для Q1 (t + 1): 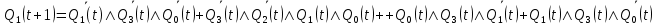 (3) (3)
 Рисунок 7 – Карта Карно для МДНФ функции Q0(t + 1)
 Рисунок 8 – Карта Карно для МКНФ функции Q0(t + 1) Из рисунков 7 и 8 видно, что и МКНФ, и МДНФ описывается одной переменной, поэтому нет никакой разницы, какую функцию использовать. Запишем МКНФ для Q0(t + 1):  (4) (4)Реализация счетчика с оптимальной схемой управленияС помощью программы Logisim по полученным МДНФ и МКНФ функциям составим схему, реализующую счетчик с оптимальной схемой управления (рис. 9). 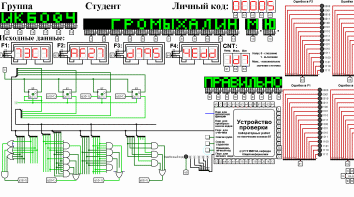 Рисунок 9 – тестирование счетчика с оптимальным управлением С помощью программы Logisim составим схему, реализующую счетчик на преобразователе кодов (рис. 10). 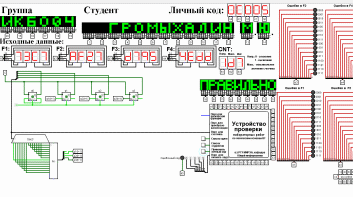 Рисунок 10 – тестирование счетчика на преобразователе кодов Итог: тестирование показало, что все собранные схемы работают правильно. ВыводыРеализовал счетчик двумя способами: с оптимальной схемой управления и с использованием преобразователя кодов. Протестировал работу схем и убедился в их правильности. Информационные источники1. Смирнов С.С., Карпов Д.А. Информатика: Методические указания по выполнению практических работ / С.С. Смирнов, Д.А. Карпов – М., МИРЭА – Российский технологический университет, 2020. – 102 с. 2. Документация программы Logisim : [сайт]. – URL: http://cburch.com/logisim/ru/docs.html (дата обращения: 02.10.21). – Режим доступа: свободный. – Текст: электронный. 3. Лекции по информатике. Доцент кафедры ОИ, к.т.н. Г. Б. Воронов. МИРЭА – Российский технологический университет. 2021. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||




 *
* 0
0 0
0 1
1 1
1 1
1 1
1
 1
1 *
* 1
1 0
0 0
0 0
0 0
0
 1
1 1
1 1
1 0
0 *
* 0
0 0
0 00
00 1
1 01
01 1
1 11
11 10
10 0
0