Интерполяция и аппроксимация экспериментальных данных. ЛР1. Отчет по лабораторной работе 1 По дисциплине "Математические методы обработки результатов экспериментов"

• Название: Отчет по лабораторной работе 1 По дисциплине "Математические методы обработки результатов экспериментов"
• Анкор: Интерполяция и аппроксимация экспериментальных данных
• Дата: 05.05.2023
• Размер: 101.88 Kb.
• Имя файла: ЛР1.docx
• Тип: Отчет; #1111320

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования "Уфимский государственный нефтяной технический университет"
Кафедра "Математика"
Отчет по лабораторной работе №1

По дисциплине "Математические методы обработки результатов экспериментов"

"Интерполяция и аппроксимация экспериментальных данных"
Вариант №2


Выполнил: студент гр. БГБ-21-02 Абдуллин А.

Проверил: доцент Лазарев В. А.
Уфа, 2023
Дано:

Таблица 1 – Сеточная функция.

X	8	12	16	20	24	28	32	36	40	44	48	52	56
F	-456	-601	-668	-693	-720	-746	-815	-810	-834	-812	-927	-910	-864

Задача 1:

Найти интерполирующую функцию, используя метод Лагранжа и метод Ньютона.

Решение:

1. 
   Метод Лагранжа
   

Найдем интерполирующую функцию, используя полином четвертой степени. Для этого выберем 5 равноотстоящих точек:
Таблица 2 – Равноотстоящие точки, выбранные из начальной сеточной функции.

	1	2	3	4	5
X	8	20	32	44	56
F	-456	-693	-815	-812	-864

;

;

;

;

;

;
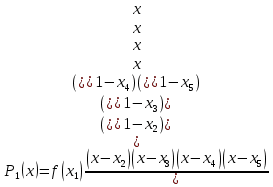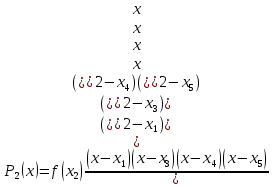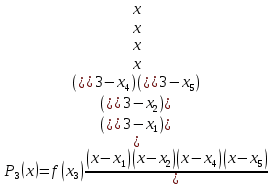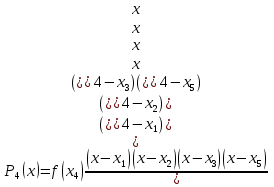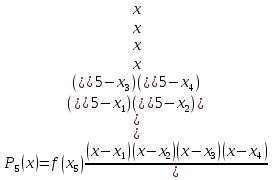Подставим значение:

;

;

;

;

;

;

Итоговый интерполяционный полином:


Проверка:
;

;

;

;

;

Как видно из проверки все значение вычисленные по интерполирующей функции совпали со значениями узлов заданной сеточной функции
Для наглядности построим графики по исходным данным и интерполирующей функции с помощью программного обеспечения Excel:
График 1 – График, построенный по исходной сеточной функции.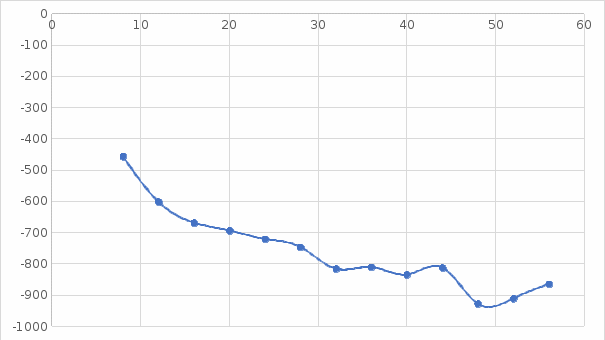


График 2 – График, построенный по расчетам интерполирующей функции.

X	8	12	16	20	24	28	32	36	40	44	48	52	56
f	-456	-539,342	-620,811	-693	-750,848	-791,638	-815	-822,909	-819,687	-812	-808,86	-821,626	-864

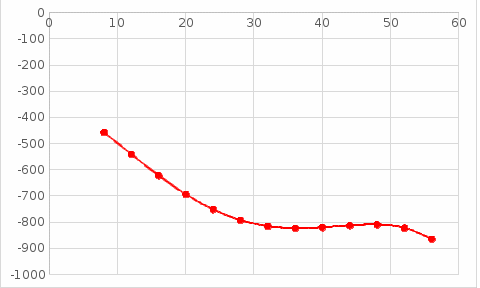Совместим оба графика для визуального сравнения.
График 3 – Совмещенные графики.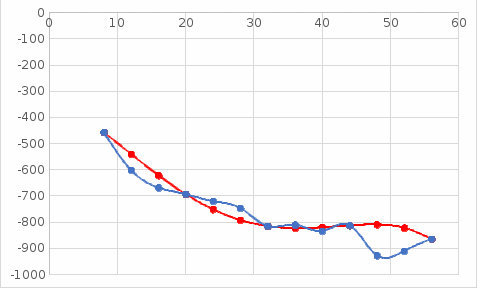


2. Метод Ньютона

Найдем интерполирующую функцию, используя всё также полином четвертой степени. Для этого выберем те же самые 5 равноотстоящих точек, что и при расчете методом Лагранжа:
Таблица 2 – Равноотстоящие точки, выбранные из начальной сеточной функции.

	1	2	3	4	5
X	8	20	32	44	56
F	-456	-693	-815	-812	-864

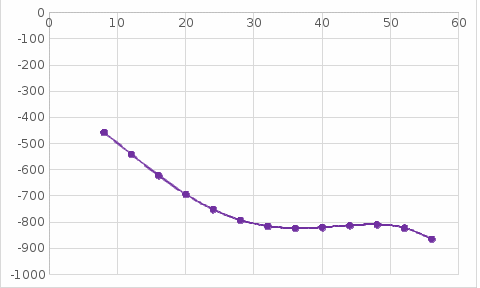
Запишем полином в виде:

;
;

;

;

;

;

;

;

;

;

;
Подставим значение: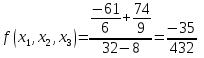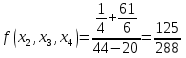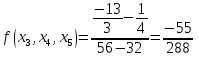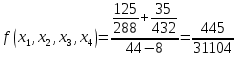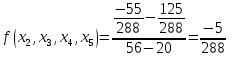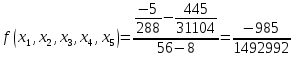
;

;

;

;

;

;

;

;

;

;
;
Итоговый интерполяционный полином:


Проверка:
;

;

;

;

;
Как видно из проверки все значение вычисленные по интерполирующей функции совпали со значениями узлов заданной сеточной функции
Для наглядности построим графики по исходным данным и интерполирующей функции с помощью программного обеспечения Excel:

График 4 – График, построенный по расчетам интерполирующей функции.

X	8	12	16	20	24	28	32	36	40	44	48	52	56
f	-456	-539,342	-620,811	-693	-750,848	-791,638	-815	-822,909	-819,687	-812	-808,86	-821,626	-864

Совместим оба графика для визуального сравнения.
График 5 – Совмещенные графики.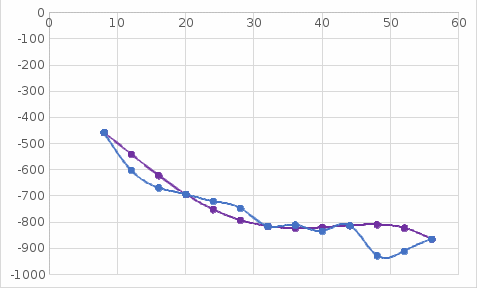



Сумма квадратов отклонений (абсолютных погрешностей) = 31201,59.

Задача 2:

Необходимо по исходным данным подобрать вид аппроксимирующей функции.

X	8	12	16	20	24	28	32	36	40	44	48	52	56
F	-456	-601	-668	-693	-720	-746	-815	-810	-834	-812	-927	-910	-864

Решение:

Изобразим табличные данные графически: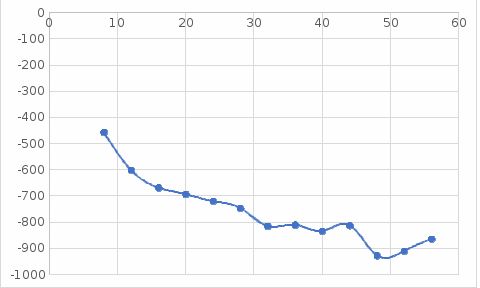


График 6 – График, построенный по исходной сеточной функции.

Из рисунка видно, что сразу нельзя определить вид аппроксимирующей функции(имеется облако точек, не имеющих определенную последовательность). В качестве эмпирической формулы для аппроксимирующей функции можно принять квадратичную или линейную функции :
1)


Имеем m=2, n = 13 (m – степень полинома и n – количество узлов). Запишем критерий минимизации

Запишем частные производные по коэффициентам





Раскроем скобки и получим систему






n=13.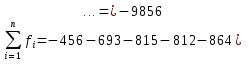












-13660224
Получаем систему уравнений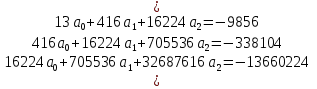


Решаем её с помощью метода Крамера






Т.о. получим аппроксимирующую функцию для исходной сеточной функции

Построим график аппроксимирующей функции по исходным значениям X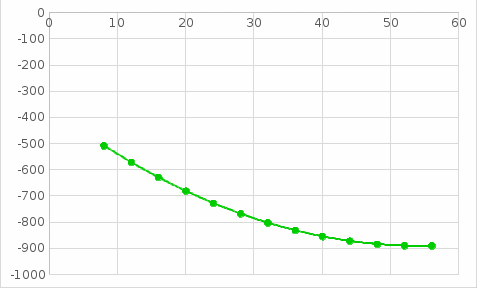


График 7 – График, построенный по аппроксимирующей функции

X	8	12	16	20	24	28	32	36	40	44	48	52	56
F	-456	-601	-668	-693	-720	-746	-815	-810	-834	-812	-927	-910	-864
f	-506,82	-570,38	-628,18	-680,22	-726,5	-767,02	-801,78	-830,78	-854,02	-871,5	-883,22	-889,18	-889,38

График 8 – Совмещенные графики.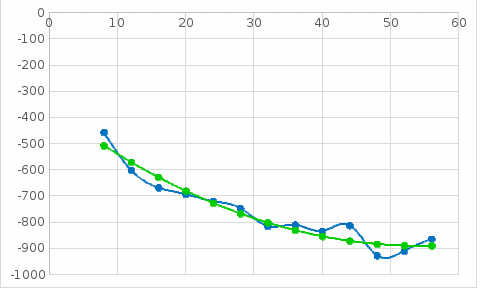

X	8	12	16	20	24	28	32	36	40	44	48	52	56
F	-456	-601	-668	-693	-720	-746	-815	-810	-834	-812	-927	-910	-864
f	-506,82	-570,38	-628,18	-680,22	-726,5	-767,02	-801,78	-830,78	-854,02	-871,5	-883,22	-889,18	-889,38
Абс погр-ть, |F-y|	50,82	30,62	39,82	12,78	6,5	21,02	13,22	20,78	20,02	59,5	43,78	20,82	25,38
Относ.погр-ть,|F-y|/F *100%	-0,111	-0,051	-0,060	-0,018	-0,009	-0,028	-0,016	-0,026	-0,024	-0,073	-0,047	-0,023	-0,029

Сумма квадратов отклонений (абсолютных погрешностей) = 13295,24.
2) Линейная аппроксимация
Имеем m=1, n = 13 (m – степень полинома и n – количество узлов). Запишем критерий минимизации

Запишем частные производные по коэффициентам



Раскроем скобки и получим систему




n=13.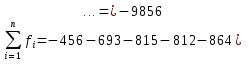






Получаем систему уравнений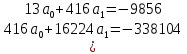


Решаем её с помощью метода Крамера



Т.о. получим аппроксимирующую функцию для исходной сеточной функции



Построим график аппроксимирующей функции по исходным значениям X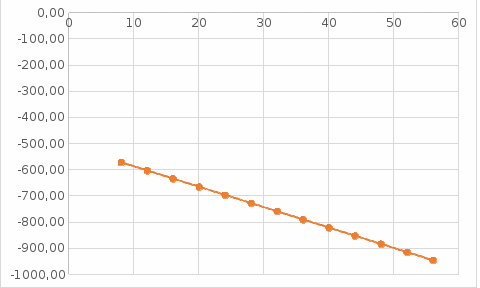


График 8 – График, построенный по аппроксимирующей функции

X	8	12	16	20	24	28	32	36	40	44	48	52	56
F	-456	-601	-668	-693	-720	-746	-815	-810	-834	-812	-927	-910	-864
f	-570,97	-602,16	-633,36	-664,56	-695,76	-726,96	-758,15	-789,35	-820,55	-851,75	-882,95	-914,14	-945,34

График 9 – Совмещенные графики.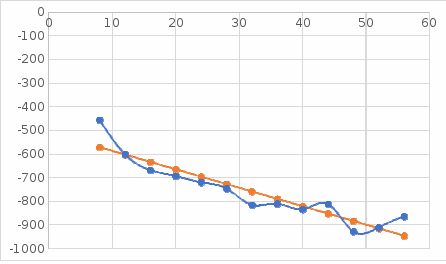

Сумма квадратов отклонений (абсолютных погрешностей) = 30170,57.
Выводы: Интерполяционный многочлен четвертой степени показывает большую погрешность, что говорит о недостаточной точности экспериментальных данных, точно отражающих зависимость у от х. Аппроксимация квадратичным многочленом дает очень малые погрешности, что также свидетельствует о точности экспериментальных данных и отчетливой выраженности тенденции. Линейная аппроксимация дает также большие погрешности. На основе проведенного анализа можно утверждать, что наиболее адекватным приближением будет интерполяция квадратичным многочленом.