ОТУ (ЛР 1). Отчет по лабораторной работе 1 по дисциплине Основы теории управления
 Скачать 259.5 Kb.
|
|
Министерство образования Российской федерации ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра автоматизированных систем управления (АСУ) ОТЧЕТ По лабораторной работе № 1 по дисциплине «Основы теории управления» Выполнил:Студент__________ 230105 28.03.2008 2008 1. ЦЕЛЬ РАБОТЫ Целью лабораторной работы является изучение и приобретение практических навыков работы с моделями и частотными и переходными характеристиками типовых динамических звеньев систем управления. 2. ОСНОВНЫЕ СООТНОШЕНИЯ В общем случае какой-либо объект в теории автоматического управления описывается передаточной функцией, содержащей полиномы от р произвольного порядка в числителе и знаменателе. Если передаточная функция объекта содержит простой множитель только в числителе либо в только в знаменателе, то такой объект называется типовым динамическим звеном. К  лассификацию типовых звеньев удобно осуществить, рассматривая различные частные формы дифференциального уравнения Значения коэффициентов уравнения (1) и названия для наиболее часто встречающихся звеньев приведены в таблице 1. Как известно, звенья, у которых коэффициенты а2 0 и b1 0 , обладают статизмом, т.е. однозначной связью между входной и выходной переменными в статическом режиме. Другие виды звеньев, у которых коэффициенты а2 0, а1 0 и а0 0, обладают инерционностью (замедлением). Таблица 1
3. РЕЗУЛЬТАТЫ РАБОТЫ Классификацию типовых звеньев удобно осуществить, рассматривая различные частные формы дифференциального уравнения. Пропорциональное (безынерционное) звено описывается уравнением  и имеет передаточную функцию  .Параметр k называется коэффициентом передачи звена и может иметь любую размерность. Инерционное (апериодическое) звено 1-го порядка Описывается дифференциальным уравнением вида 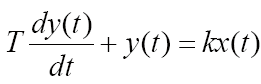 Перейдя к изображениям, была получена передаточная функция 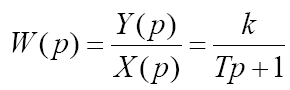 Идеальное дифференцирующее звеноописывается уравнением 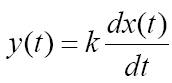 а его передаточная функция имеет вид  .Идеальное интегрирующее звеноописывается таким уравнением  причём передаточная функция представима в виде 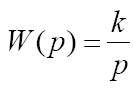 Реальное дифференцирующее звено Такое звено является последовательным соединением дифференцирующего и инерционного звеньев, а его передаточная функция имеет вид 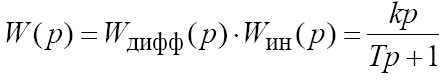 Инерционное апериодическое звено 2-го порядка В общем случае звено второго порядка описывается уравнением 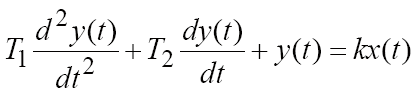 Передаточная функция апериодического звена 2-го порядка имеет вид 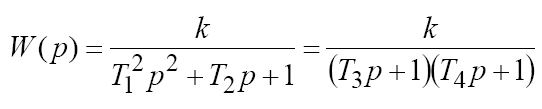 где 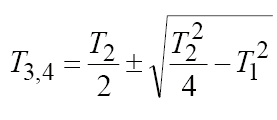 .Из выражения передаточной функции такого типа звена видно, что апериодическое звено второго порядка состоит из двух инерционных (апериодических) звеньев с эквивалентными постоянными времени Т3, Т4, поэтому логарифмические частотные характеристики этих инерционных звеньев складываются. Инерционное колебательное звено 2-го порядка Это звено получается при комплексных сопряжённых полюсах передаточной функции. Передаточную функцию звена удобнее записать в виде: 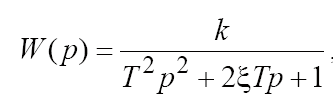 причём при 0 < ξ < 1 звено колебательное, а при ξ ≥ 1 звено уже является апериодическим 2-го порядка. В данной работе были рассмотрены все эти типы динамических типовых звеньев. Коэффициенты их уравнений представлены в таблице 2. Таблица 2
Далее для каждого звена по его передаточной функции запишем операторное уравнение. Так как параметр k = 10 (коэффициент перед b1), то операторные уравнения запишутся в виде: Безынерционное (пропорциональное) звено W(s) =  Инерционное 1-го порядка (апериодическое) звено W(s) =  Инерционное 2-го порядка (апериодическое) звено W(s) =  Инерционное 2-го порядка (колебательное) звено W(s) =  Идеальное интегрирующее звено W(s) =  Реальное интегрирующее звено W(s) =  Идеальное дифференцирующее звено W(s) =  Реальное дифференцирующее звено W(s) =  Для инерционных звеньев по логарифмическим частотным характеристикам определяем частоты сопряжения и среза. Инерционное 1-го порядка (апериодическое) звено W(s)ср = 99,5 рад/с Инерционное 2-го порядка (апериодическое) звено W(s)ср = 70,93 рад/с Инерционное 2-го порядка (колебательное) звено W(s)ср = 16,48 рад/с Значения полюсов и нулей передаточных функций, а также их влияние на переходный процесс, представлены на графиках ниже. Инерционное 2-го порядка (апериодическое) На графике представлены нули функции (крестиками). 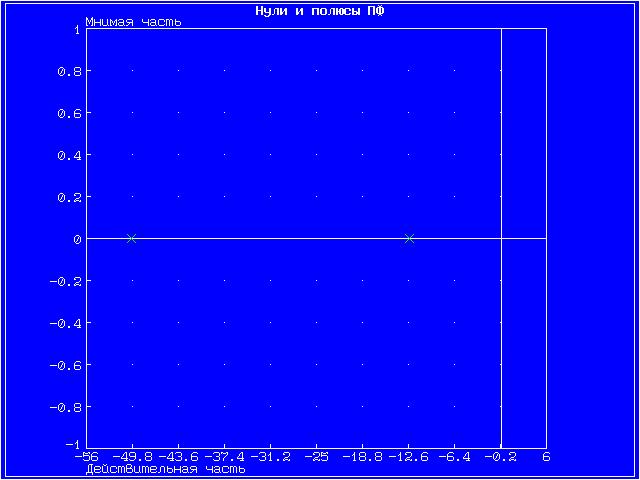 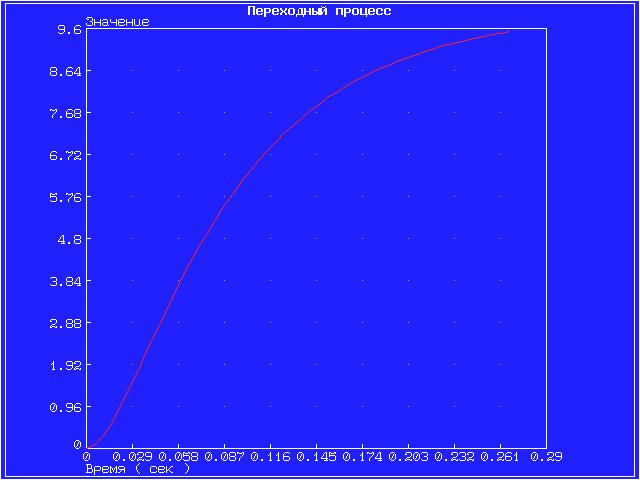 Инерционное 2-го порядка (колебательное) На графике представлены полюсы функции. 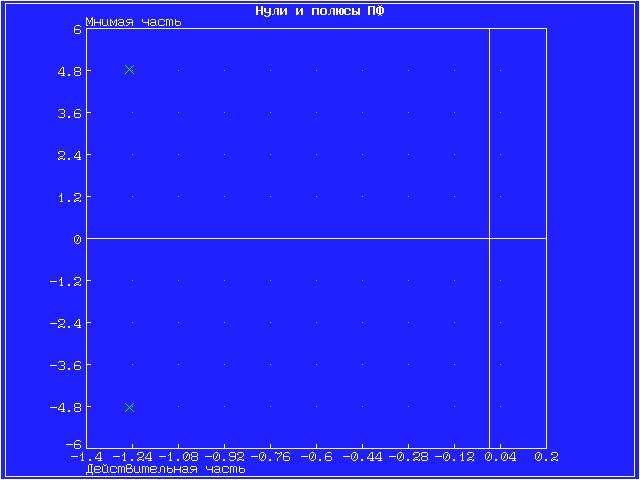 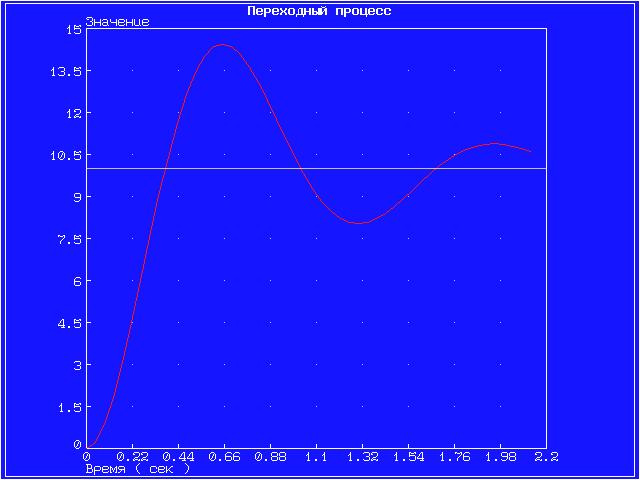 Графики амплитудной фазовой характеристики (АФХ), логарифмической амплитудной частотной характеристики (ЛАЧХ) и логарифмической фазовой частотной характеристики (ЛФЧХ). Точная ЛАЧХ системы управления рассчитывается по формуле:  где А — коэффициент наклона ЛАХЧ. Точная ЛФЧХ рассчитывается как сумма аргументов от АФХ звеньев, составляющих САУ, то есть:  где k — номер звена, n — общее количество звеньев САУ. Графики ЛАЧХ и ЛФЧХ представлены на одной системе координат. Красный график — логарифмическая амплитудная частотная характеристика, зелёный график — логарифмическая фазовая частотная характеристика. График амплитудной фазовой характеристики представлен на отдельном рисунке. Инерционное 2-го порядка (апериодическое) 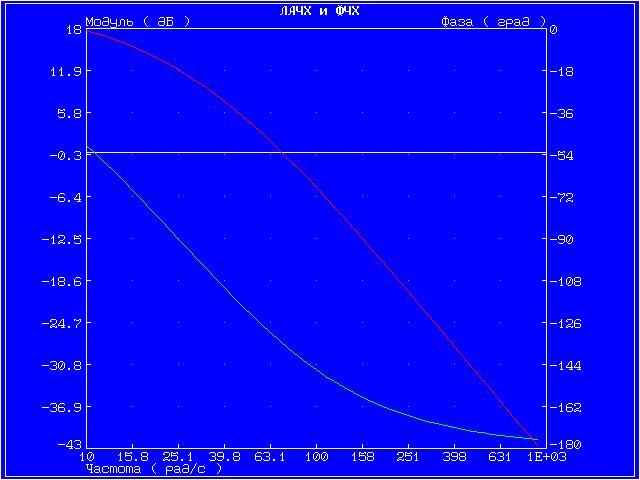 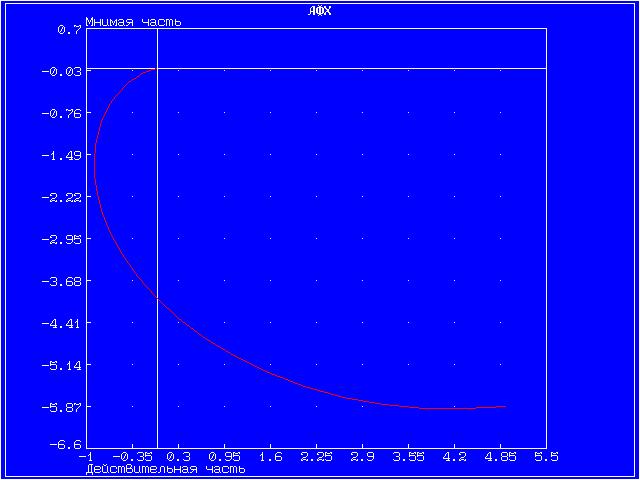 Инерционное 2-го порядка (колебательное) 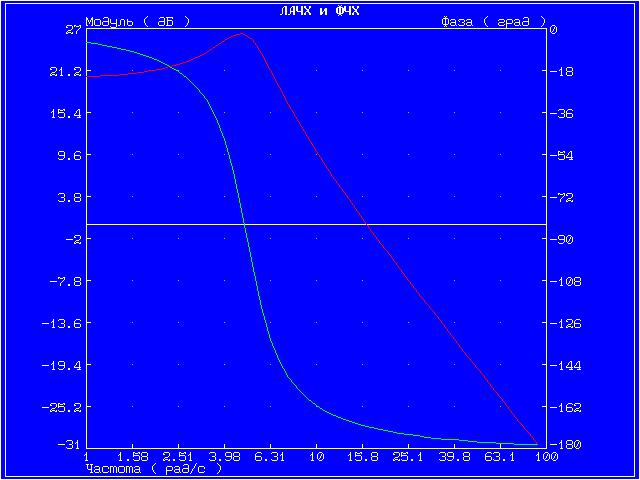 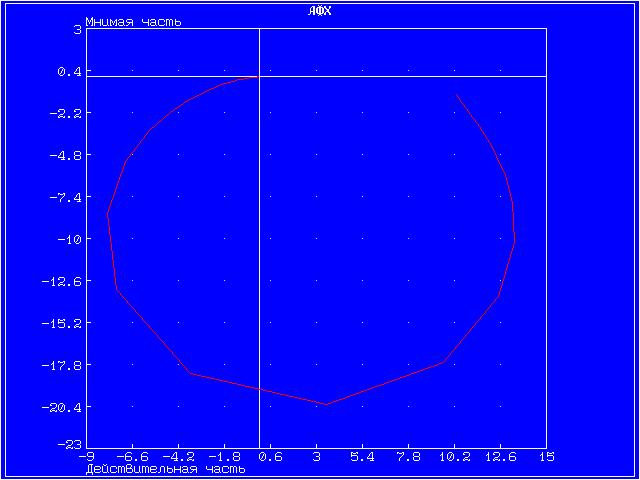 4. ВЫВОДЫ В результате проделанной работы были изучены модели восьми звеньев, но более подробно исследовались звенья 2-го порядка. Для звена по его передаточной функции записано операторное уравнение. Построены графики переходных функций и определены нули и полюсы динамического звена. С помощью логарифмических частотных характеристик определены частоты среза и сопряжения. Колебательное звено имеет более сложные характеристики и менее гладкие графики АФХ, ЛАЧХ, ЛФЧХ. Колебания малых частот «пропускаются» звеном с отношением амплитуд выходной и входной величин, близким к статистическому коэффициенту передачи звена k. Колебания больших частот проходит с сильным ослаблением амплитуды. 5. ВОПРОСЫ 1. Что такое передаточная функция? Любая система, которую можно возбудить гармоническими колебаниями, будет реагировать на них также каким-то колебательным движением. Существует характеристика, которая определяет преобразование амплитуды и сдвиг фазы выходного колебания по отношению к входному. Такой характеристикой может быть следующее отношение  .Функцию  называют характеристикой реакции линейной системы на показательное возмущение или параметрической передаточной функцией.2. С какой целью и каким образом выделяют типовые динамические звенья САУ? Для исследования стационарных линейных систем удобно ввести элементарные типовые стационарные звенья, передаточными функциями которых являются отдельные простейшие множители в формуле 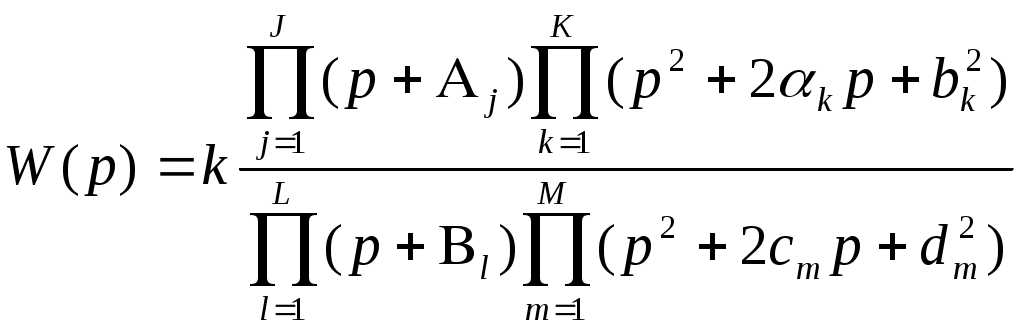 ,где r – любое целое число. Типы звеньев САУ различаются по виду передаточной функции, определяющей все их динамические свойства и характеристики. К настоящему времени принято типовые динамические звенья САУ разделять на обыкновенные и особые, которые в свою очередь делятся на три группы: позиционные, интегрирующие и дифференцирующие. 3. Как влияет безынерционное звено на амплитуду и фазу синусоидального сигнала? При включении в цепь безынерционного звена амплитуда синусоидального входного сигнала уменьшается, а фаза наоборот увеличивается. 4. Какие звенья называются апериодическими? Апериодическое звено – это звено динамические свойства которого, характеризуются постоянной времени Т, это время, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости изменения ее в начальный момент времени. 5. Как проходят через инерционное звено первого порядка гармонические сигналы низкой и высокой частоты? При прохождении гармонического сигнала низкой частоты он усиливается, высокой частоты наоборот уменьшается. 6. Какие звенья называются колебательными? Звенья, у которых постоянные времени Т1<2Т2, имеют колебательный процесс и называются колебательными. Корни характеристического уравнения этого типового динамического звена являются комплексными. 7. При каком соотношении между постоянными времени Т1 и Т2 инерционное звено второго порядка имеет апериодический процесс и при каком – колебательный? Если Т1≥2Т2, то инерционное звено 2-го порядка имеет апериодический переходный процесс. Характеристическое уравнение, соответствующие этому звену имеет не комплексные, а отрицательные действительные корни. Если Т1<2Т2, то звено имеет колебательный процесс, т.к. полюсы этого типового динамического инерционного звена 2-го порядка являются комплексными. 8. Какие звенья называются интегрирующими? Рассмотрим звено с передаточной функцией  В таком звене при  преобладает инерционное запаздывание, т.е. интегрирование. Поэтому такое звено часто называют интегрирующим.9. Какие звенья называются дифференцирующими? Рассмотрим звено с передаточной функцией В таком звене при  преобладает форсирование, т.е. дифференцирование. Такое звено называют дифференцирующим. 10. Чем отличаются идеальные дифференцирующее и интегрирующее звенья от реальных? Выходная величина идеального интегрирующего звена пропорциональна интегралу от входной величины, коэффициент передачи звена имеет размерность с-1. А реальное интегрирующее звено обладает инерционностью, поэтому его выходная величина не равна точно интегралу от входной величины. В идеальном дифференцирующем звене выходная величина пропорциональна производной от входной величины, а в реальном дифференцирующем звене эта пропорциональность не соблюдается. Любые реальные звенья не являются элементарными, т.к. их можно заменить последовательным соединением других типовых динамических звеньев. 11. Почему дифференцирующие звенья плохо пропускают медленно меняющиеся входные сигналы? Дифференцируемые звенья плохо пропускают медленно меняющиеся входные сигналы, так как они реагируют только на изменение входной величины. |