тмм лаба. тмм лаба гуд. Отчет по лабораторной работе 1 по дисциплине Теория машин и механизмов
 Скачать 7.91 Mb. Скачать 7.91 Mb.
|
|
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра ПМИГ ОТЧЕТ по лабораторной работе №1 по дисциплине «Теория машин и механизмов» “Исследование передаточного механизма”
Санкт-Петербург 2023 Протокол к лабораторной работе №1 Установка №1 Кривошипно-шатунный механизм   1.Расчет подвижности механизма. Формула Чебышева: W=3*2-2*2-1=1 Формула Сомова-Малышева: W=6*n – 5*P5 – 4*P4 – 3*P3 – 2* P2 – P1 => W=6*n – 5*P5 – 4*P4=6*2– 5*2– 3*1= – 1; Вывод: механизм по Чебышеву обладает 1 степенью подвижности. Это значит, что достаточно задать одну координату любому звену механизма в системе координат, чтобы определить положения всех остальных звеньев. Такой механизм является оптимальным, так как он подвижен (W>0) и его можно привести в движение одним приводом. 2. Название всех кинематических пар 4-ого и 5-ого классов n – подвижные звенья; n=2 – вал и стойка Pн – низшие кинематические пары; Pн= 2: P5- вал и стойка, P5- ползун и стойка Pв - высшие кинематические пары; Pв= 1: P4- шатун и кривошип 3. Кинематическая схема. Передаточное число пар и всего механизма. 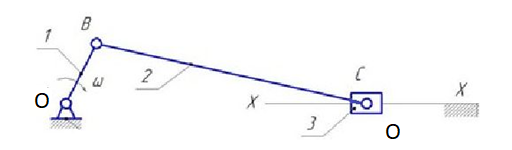 O – стойка 1 – кривошип 2 – шатун 3 – ползун Передаточное число вычисляется только при одинаковом типе движения, например, в зубчатой передачи передаточное число – это отношения чисел зубьев колес. В механизме нет передаточного числа, так как механизм преобразует вращательное движение кривошипа в поступательное движение ползуна. Установка №2 Механизм с мальтийским крестом Количество зубчиков: 44,28,22,4; количество пазов мальтийского креста: 6   1.Расчет подвижности механизма. Формула Чебышева: W= 3n – 2*Pн – Pв= 3*4-2*4-3=1 Формула Сомова-Малышева: W=6*n – 5*P5 – 4*P4=6*4 – 5*4 – 4*3= –8 Вывод: механизм по Чебышеву обладает 1 степенью подвижности. Это значит, что достаточно задать одну координату любому звену механизма в системе координат, чтобы определить положения всех остальных звеньев. 2. Название всех кинематических пар 4-ого и 5-ого классов n=4- червяк, колёса, мальтийский крест Pн= 4; названия: вал и стойка Pв = 3; Названия: I- червячная передача, II- цилиндрическая передача, III-мальтийский крест; 3.Передаточное число: U12=Z2:Z1=28:4=7 U34=Z4:Z3=44:22=2 U56=Z6:Z5=6:44=0,14 U16=7*2*0,14=1,96 Такой механизм является оптимальным, так как он подвижен (W>0) и его можно привести в движение одним приводом. Кинематическая схема 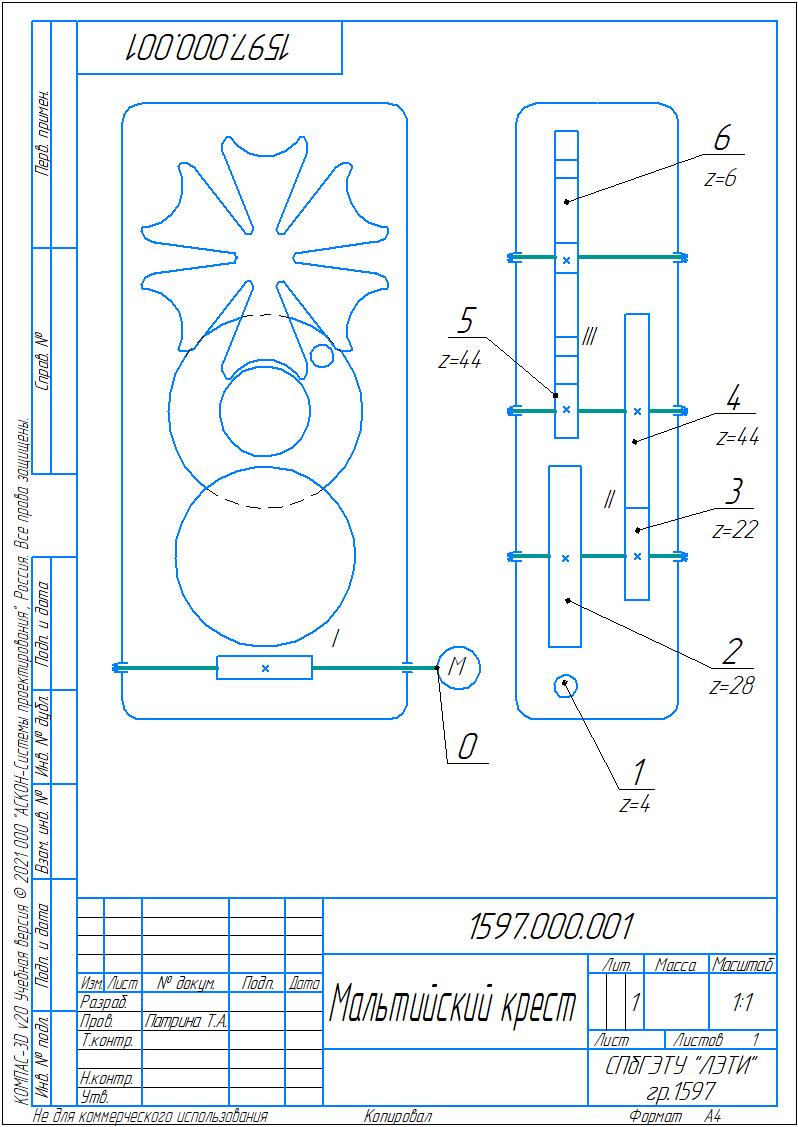 0-стойка,1-червяк, 2-шестерёнка, 3,4-сдвоенная шестеренка, 5,6-мальтийский крест Установка №3 Зубчатая передача цилиндрического типа Количество зубчиков: 2х50, 2х30, 65   1. Расчет подвижности механизма. Формула Чебышева: W= 3n – 2*Pн – Pв= 3*4-2*4-3=1 Формула Сомова-Малышева: W=6*n – 5*P5 – 4*P4=6*4 – 5*4 – 4*3= –8 Вывод: механизм по Чебышеву обладает 1 степенью подвижности. Это значит, что достаточно задать одну координату любому звену механизма в системе координат, чтобы определить положения всех остальных звеньев. 2. Название всех кинематических пар 4-ого и 5-ого классов n=4-вал и стойка Pн= 4, Название: вал и стойка Pв = 3 Название: I, II, III- цилиндрическая передача 3. Передаточное число U12=Z2:Z1=30:65=0,46 U23=Z3:Z2=30:30=1 U45=Z5:Z4=50:50=1 U15=0,46 Такой механизм является оптимальным, так как он подвижен (W>0) и его можно привести в движение одним приводом. Кинематическая схема 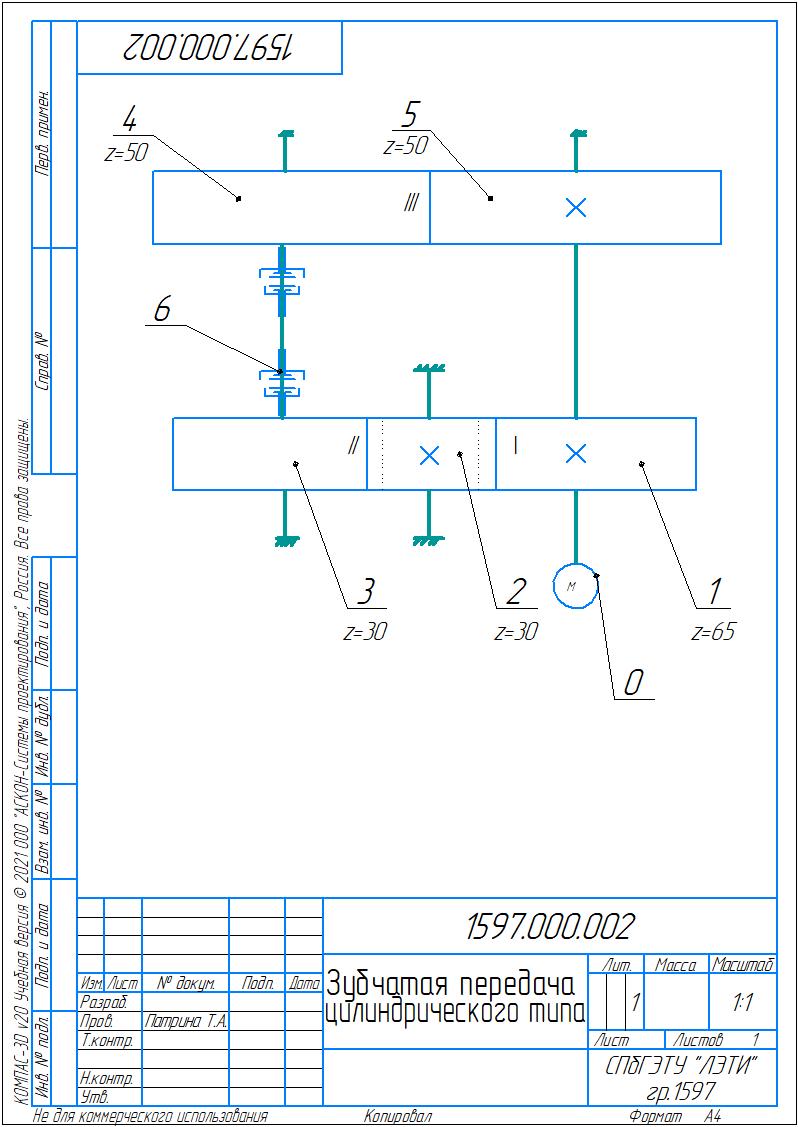 0-стойка, 1,2,3,4,5-шестеренки, 6-муфта Выводы и результаты: Мы овладели методами анализа структуры механизма Все плоские механизмы по Чебышеву обладают 1 степенью подвижности. Это значит, что достаточно задать одну координату любому звену механизма в системе координат, чтобы определить положения всех остальных звеньев. Передаточные числа можно определить не для всех механизмов. Если механизм преобразует одно движение в другое, то для него нельзя посчитать передаточное число. Передаточное число для механизма с мальтийским крестом равно = 1,96, передаточное число для зубчатой передачи цилиндрического типа = 0,46. Были построены и изучены кинематические схемы для данных установок, также благодаря которым было посчитано передаточное число. |
