Адаев Жарас АИСУ 20-13 ОСИПИ 1 лаб. Отчет по лабораторной работе 1 По дисциплине
 Скачать 179.74 Kb. Скачать 179.74 Kb.
|
|
Решение
Определим среднюю информацию, содержащуюся в одной букве передаваемого текста, т.е. энтропия на одну букву: 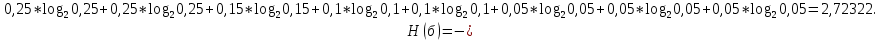 Неопределенность на одну букву: 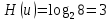 Определим среднее число элементарных символов на букву как произведение количества символов кода на вероятность появления данной буквы: 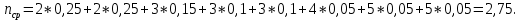 Информация на один элементарный символ: 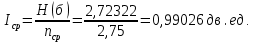 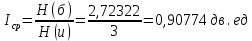 Задача 7. Источник сообщений выдает целые xi (i=1…….12) значения случайной величины Х, распределение которой подчиняется закону Пуассона с параметром α=3. Закодировать сообщение методом Шенно - Фано. Определить: 1) Пригодность кода для передачи сообщений в смысле их однозначного кодирования. 2) На сколько код Шенно-Фано длиннее оптимального (в процентах). Решение
Находим вероятности по формуле Пуассона: 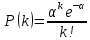 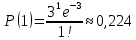 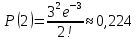 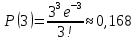 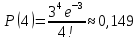 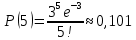 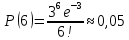 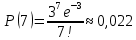 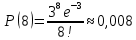 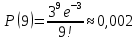 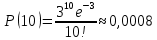 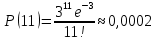 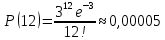 Определим среднюю информацию, содержащуюся в одной букве передаваемого текста, т.е. энтропия на одну букву: 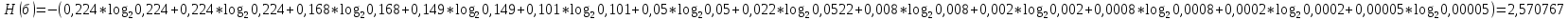 Неопределенность на одну букву: 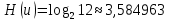 Определим среднее число элементарных символов на букву как произведение количества символов кода на вероятность появления данной буквы: 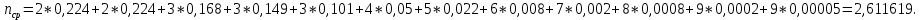 Информация на один элементарный символ: 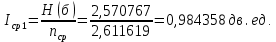 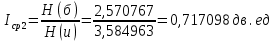 Таким образом, информация на один символ близка к своему верхнему пределу 1. Следовательно, построенный код в целом отвечает принципу оптимальности. В случае кодирования простым двоичным кодом каждая буква изображается пятью двоичными знаками и информация на один символ 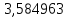 дв.ед. дв.ед.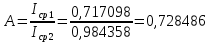 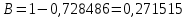 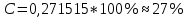 На 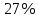 код Шенно-Фано длиннее оптимального. код Шенно-Фано длиннее оптимального.Задание 8. Построить код Шенно-Фано двумя способами разбиения множества групп на подгруппы для символов источника сообщений появляющихся с вероятностями, заданными таблицей
1 способ: первая группа . p(a6)+ p(a3)+ p(a5) = 0,58. Вторая группа . p(a8)+ p(a4)+ p(a2)+ p(a1)+ p(a7) =0,42 2 способ: первая группа . p(a6)+ p(a3) = 0,42 Вторая группа . p(a5)+ p(a8)+ p(a4)+ p(a2)+ p(a1)+ p(a7 ) = 0,58 Провести сравнительный анализ результатов решения двумя способами. Решение
Определим среднюю информацию, содержащуюся в одной букве передаваемого текста, т.е. энтропия на одну букву: 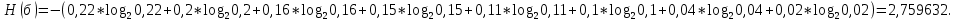 Неопределенность на одну букву: 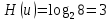 Определим среднее число элементарных символов на букву как произведение количества символов кода на вероятность появления данной буквы: 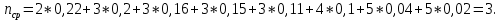 Информация на один элементарный символ: 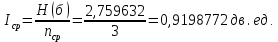 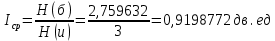
Определим среднюю информацию, содержащуюся в одной букве передаваемого текста, т.е. энтропия на одну букву: 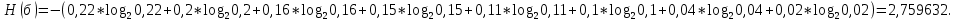 Неопределенность на одну букву: 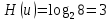 Определим среднее число элементарных символов на букву как произведение количества символов кода на вероятность появления данной буквы: 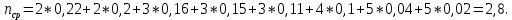 Информация на один элементарный символ: 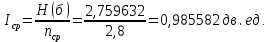 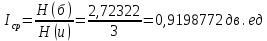 Таким образом, информация на один символ близка к своему верхнему пределу 1. Следовательно, построенный код в целом отвечает принципу оптимальности. В случае кодирования простым двоичным кодом каждая буква изображается пятью двоичными знаками и информация на один символ 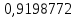 дв.ед. дв.ед.Вывод: В данном задании были построены две таблицы, различными способами, 1 способ: первая группа. p(a6) + p(a3) + p(a5) = 0,58. Вторая группа. p(a8) + p(a4) + p(a2) + p(a1) + p(a7) =0,42 2 способ: первая группа. p(a6) + p(a3) = 0,42 Вторая группа. p(a5) + p(a8) + p(a4) + p(a2) + p(a1) + p (a7)= 0,58 Была найдена средняя информация, содержащаяся в одной букве, H(u) = 2,759, неопределенность на одну букву H(u) = 3, среднее число элементарных символов 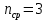 , информация на один элементарный символ: , информация на один элементарный символ: 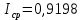 , , 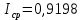 , для второй таблицы было найдено средняя информация, содержащаяся в одной букве, H(u) = 2,7596, неопределенность на одну букву H(u) = 3, среднее число элементарных символов , для второй таблицы было найдено средняя информация, содержащаяся в одной букве, H(u) = 2,7596, неопределенность на одну букву H(u) = 3, среднее число элементарных символов 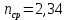 , информация на один элементарный символ: , информация на один элементарный символ: 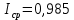 , , 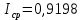 . .Задание 9. Построить оптимальный код сообщения, состоящего из: a) пяти равновероятных букв; b) шести равновероятных букв; с) семи равновероятных букв; d) восьми равновероятных букв. Дать оценку эффективности построенных кодов. В каких случаях код, построенный для первичного алфавита с равновероятным появление букв, окажется самым эффективным? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
