Адаев Жарас АИСУ 20-13 ОСИПИ 1 лаб. Отчет по лабораторной работе 1 По дисциплине
 Скачать 179.74 Kb. Скачать 179.74 Kb.
|
|
Некоммерческое акционерное общество «Алматинский университет энергетики и связи имени Гумарбека Даукеева»  ОТЧЕТ по лабораторной работе № 1 По дисциплине ______ Основы сбора и передачи информации_________ На тему: «Основы теории кодирования сообщений» Образовательная программа 6В07108 – «Автоматизация и управление»__ Выполнил Адаев Жарас Группа АИСУ-20-13 (Ф.И.О.) ПринялВодолазкина Н. (ученая степень, звание, Ф.И.О.) «»__2022 г. (оценка) (подпись) Алматы 2022 Лабараторная работа №1. Основы теории кодирования сообщений Цель работы: изучить понятия кодирования и декодирования информации, метод Шенно-Фано. Краткие теоретические сведения Преобразование информации из одной формы представления (знаковой системы) в другую называется кодированием. Понятие кодирование означает преобразование информации в форму, удобную для передачи по определённому каналу связи. Декодирование – восстановление принятого сообщения из кодированного вида в вид доступный для потребителя. Одно и тоже сообщение можно закодировать различными способами. Необходимо найти оптимальный способ кодирования, при котором на передачу сообщения тратится минимальное время. Если на передачу каждого элементарного символа (0 или 1) тратится одно и тоже время, то оптимальным будет такой код, при котором на передачу сообщения заданной длины будет затрачено минимальное количество символов. Кодирование Шеннона-Фано: Кодирование методом Шеннона-Фано является одним из простейших методов статистического кодирования. Кодирование по Шеннону-Фано производится в соответствии с следующим алгоритмом: 1 Все символы из исходного алфавита U записывают в порядке убывания вероятностей. 2 Всю совокупность символов разбивают на две примерно равные по сумме вероятностей группы: одной из них (в группе могут быть один или более символов) присваивают значение 1, другой - 0. 3 Каждую из этих групп снова разбивают (если это возможно) на две части и каждой из частей присваивают значения 1 или 0. Данный пункт повторяется итеративно и рекурсивно до разбиения всех групп. Задача 1. Пусть алфавит источника содержит шесть элементов { A, Б, В, Г, Д, Е}, появляющихся с вероятностями Р(А) = - 0.15, Р(В) =0.1, Р(Б) = 0.25, Р(Г) = 0.13, Р(Д) = Р(Е) = 0.12. Найти энтропию такого источника, среднее число символов на одну букву при кодировании методом Ш-Ф. Решение Энтропия такого источника: Н(Х) 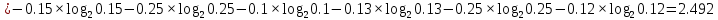 Алгоритм построения сжимающего кода Шеннона – Фано заключается в следующем:  Таблица 1. Посторение кода Ш-Ф 1. Все m символов дискретного источника располагаются в порядке убывания вероятностей их появления. 2. Образованный столбец символов делится на две группы таким образом, чтобы суммарные вероятности каждой группы мало отличались друг от друга. 3. Верхняя группа кодируется символом «1», а нижняя – «0». 4. Каждая группа делится на две подгруппы с близкими суммарными вероятностями; верхняя подгруппа кодируется символом «1», а нижняя – «0». 5. Процесс деления и кодирования продолжается до тех пор, пока в каждой подгруппе не окажется по одному символу сообщения источника. 6. Записывается код для каждого символа источника; считывание кода осуществляется слева направо. При использовании простейшего равномерного кода для кодирования шести элементов алфавита источника потребуется по три двоичных символа на каждую букву сообщения. Если же используется код Шеннона – Фано, то среднее число символов на одну букву: 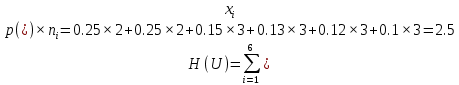 nср = 3*0,25+3*0,25+3*0,15+3*0,13+3*0,12+3*0,1 =3. что меньше, чем при простейшем равномерном коде и незначительно отличается от энтропии источника. Задача 2. Закодировать методом Шенно-Фано блоки «мы все учились понемногу чему-нибудь и как-нибудь».  Решение
Среднее число элементарных символов на букву: Ncp=2*0,37+3*0,13+3*0,125+3*0,11+3*0,08+4*0,06+4*0,052+4*0,023+4*0,05 = 2,815. Энтропия на одну букву: H(u) = - ( 0.37* log2 0.37 + 0.13* log2 0.13 + 0.125* log2 0.125+ 0.11* log2 0.11+ 0.08* log2 0.08+ 0.06* log2 0.06 + 0.06* log2 0.06 + 0.052* log2 0.052 + 0.05* log2 0.05+ 0.023* log2 0.023 ) = 2,726. Информация на один элементарный символ: Iср = H(u)/nср= 0,968. Задача 3. Сообщение состоит из последовательности букв А, B и С, вероятности которых не зависят от предыдущего сочетания букв и равны Р(А)=0,7, Р(В)=0,2, Р(С)=0,1. Провести кодирование по алгоритму ШенноФано отдельных букв и двухбуквенных сочетаний. Сравнить коды по их эффективности и избыточности. Решение
А=00; АВ=0010; ВА=1000; В=10; АС=0011; СА=1100; С=11; СВ=1110; ВС=1011; Среднее число элементарных символов на букву Ncp= 1*0,7+2*0,2+2*0,1=1,3. Энтропия на букву Н(u) = -(0,7*log2 *0,7+0,2*log2 *0,2+0.1 *log2 *0,1) = 0,115. Информация на один элементарный символ Icp=H(u)/ncp = 0,0885. Задача 4. Закодировать сообщение методом Шенно-Фано «Теория информацииКодированияМодуляции». Решение Составляется алфавит кода и для каждого символа этого алфавита и определяется вес [количество повторений символа в сообщении]. Т – 1, Е – 1, О – 5, Р – 3, И – 8, Я – 3, Н - 2, Ф - 1, М - 2, А - 2, Ц - 2, К - 1, Д - 2, В - 1, У - 1, Л – 1. Алфавит ранжируется по убыванию веса символа. И – 8, О – 5, Р – 3, Я – 3, А – 2, Д – 2, Н – 2, Ц – 2, М – 2, Т – 1, Е – 1, Ф – 1, К - 1, В – 1, У - 1, Л – 1. Далее создается таблица символов:
Используя полученную таблицу кодов, кодируется входной поток - каждый символ заменяется соответствующим кодом. 11010 11011 010 0110 00 0111 00 1010 11100 010 0110 1100 1000 1011 00 00 11101 010 1001 00 0110 010 11110 1000 1010 00 0111 1100 010 1001 111110 111111 0111 1011 00 00 Задача 5. Построить код Шенно-Фано для системы из семи букв: A, B, C, D, E, F, G, вероятности появления которых соответственно 0,1, 0,2, 0,05, 0,3, 0,05, 0,15, 0,15. Определить среднее количество разрядов на одну букву. Декодировать этим кодом последовательность: 10011101001000111101110101111000. Решение Составим таблицу кодов для символов алфавита
10011101001000111101110101111000 Используя полученную таблицу кодов декодируем заданную нам набор двоичных чисел, каждый код заменяется соответствующим символом. 100 1110 100 100 01 1110 1110 101 1110 00 Полученный результат: FEFFBEEGED Определим среднюю информацию, содержащуюся в одной букве передаваемого текста, т.е. энтропия на одну букву:  Неопределенность на одну букву:  Определим среднее число элементарных символов на букву как произведение количества символов кода на вероятность появления данной буквы:  Информация на один элементарный символ:  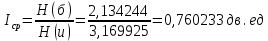 Задача 6. Провести эффективное кодирование ансамбля из восьми знаков (m=8), используя метод Шенно-Фано. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
