Адаев Жарас АИСУ 20-13 ОСИПИ 1 лаб. Отчет по лабораторной работе 1 По дисциплине
 Скачать 179.74 Kb.
|
|
Решение a) пяти равновероятных букв;
Определим среднюю информацию, содержащуюся в одной букве передаваемого текста, т.е. энтропия на одну букву: 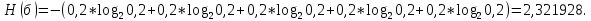 Неопределенность на одну букву: 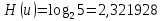 Определим среднее число элементарных символов на букву как произведение количества символов кода на вероятность появления данной буквы: 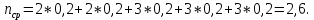 Информация на один элементарный символ: 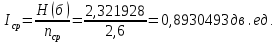 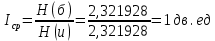 b) шести равновероятных букв;
Определим среднюю информацию, содержащуюся в одной букве передаваемого текста, т.е. энтропия на одну букву: 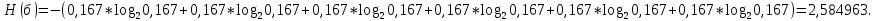 Неопределенность на одну букву: 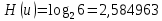 Определим среднее число элементарных символов на букву как произведение количества символов кода на вероятность появления данной буквы: 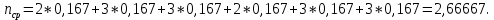 Информация на один элементарный символ: 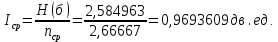 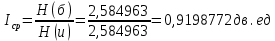 с) семи равновероятных букв;
Определим среднюю информацию, содержащуюся в одной букве передаваемого текста, т.е. энтропия на одну букву: 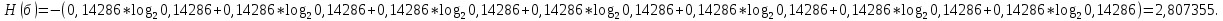 Неопределенность на одну букву: 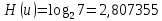 Определим среднее число элементарных символов на букву как произведение количества символов кода на вероятность появления данной буквы: 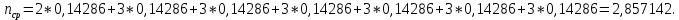 Информация на один элементарный символ: 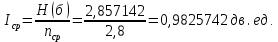 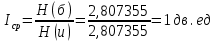 d) восьми равновероятных букв.
Определим среднюю информацию, содержащуюся в одной букве передаваемого текста, т.е. энтропия на одну букву: 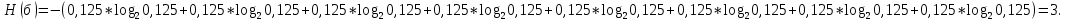 Неопределенность на одну букву: 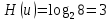 Определим среднее число элементарных символов на букву как произведение количества символов кода на вероятность появления данной буквы: 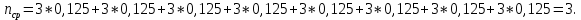 Информация на один элементарный символ: 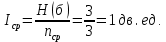 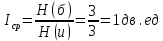 Как мы видим по четырём по четырем примерам эфективным оказался равноверятный способ. Так как равноверятным способом информация на один элементарный символ расчитали 1 . Вывод: В данном заданий необходимо было построить оптимальный код сообщения который состоит из 5 равновероятных букв, в данном случае было предоставлено еще 3 случая при шести, семи, восьми равновероятных букв, для решения необходимо было построить таблицу в которой были записаны буквы и их вероятности, таким образом получили код, определили среднюю информацию на букву H(u) = 2,321, неопределенность на одну букву H(u) = 2,3219, среднее число элементарных символов 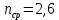 , информация на один элементарный символ:  ,  , 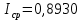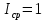таким же образом были выполнены действия и для других случаев. Вывод: В данной лабораторной работе № 1 были выполнены 9 заданий, где в каждом необходимо было поострить таблицу с символами и их вероятностями, были найдены следующие значения: средняя информация которая содержится в одной букве, неопределённость на одну букву, среднее число элементарных символов на одну букву, информация на один элементарный символ, все это необходимо было находить практически в каждом задании, построить код Шенно-Фано, была необходимость использовать формулу Пуассона 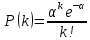 , таким образом были решены все поставленные задания. Контрольные вопросы: Что понимают под кодированием сообщения? Преобразование информации из одной формы представления (знаковой системы) в другую называется кодированием. Приведите примеры простейших кодовых сообщений. Шифр транспонирования В транспозиционном шифре буквы переставляются по заранее определённому правилу. Например, если каждое слово пишется задом наперед, то из hello world получается dlrow olleh. Другой пример — менять местами каждые две буквы. Таким образом, предыдущее сообщение станет eh ll wo ro dl. Азбука Морзе В азбуке Морзе каждая буква алфавита, цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов. Какие коды называются равномерными? Код называется равномерным (или кодом постоянной длины), если все его кодовые слова содержат одинаковое число букв (одинаковую длину слов). Что называется двоичным кодом? Двоичный код — это способ представления данных в виде кода, в котором каждый разряд принимает одно из двух возможных значений, обычно обозначаемых цифрами 0 и 1. Разряд в этом случае называется двоичным разрядом. Как можно закодировать четыре сообщения a,b,c,d, используя только два сигнала, 0 и 1? Один из вариантов кодирования может быть следующим: 00, 01, 10, 11. При таком кодировании вероятность появления сообщений не учитывалась или предполагалась равновероятность (р = 0,25). Между тем их появление в информационном тексте может происходить с различной частотой; предположим, вероятности появления сообщений равны: р = 0,4; р = 0,3; р = 0,2; р = 0,1. Учитывая вероятность сообщений, Фано предложил следующее оптимальное кодирование  Как строится код Шенно-Фано? Кодирование методом Шеннона-Фано является одним из простейших методов статистического кодирования. Кодирование по Шеннону-Фано производится в соответствии с следующим алгоритмом: 1Все символы из исходного алфавита U записывают в порядке убывания вероятностей. 2Всю совокупность символов разбивают на две примерно равные по сумме вероятностей группы: одной из них (в группе могут быть один или более символов) присваивают значение 1, другой - 0. 3Каждую из этих групп снова разбивают (если это возможно) на две части и каждой из частей присваивают значения 1 или 0. Данный пункт повторяется итеративно и рекурсивно до разбиения всех групп. Как определяется число элементарных сигналов, приходящихся на одну букву сообщения? Это произведение количества символов кода на вероятность появления данной буквы. Сформулировать основную теорему о кодировании. Теорема Шеннона об источнике шифрования показывает, что невозможно сжать данные настолько, что оценка кода (среднее число бит на символ) меньше чем энтропия Шеннона исходных данных, без потери точности информации. Тем не менее можно получить код, близкий к энтропии Шеннона без значительных потерь. Что называется декодирование сообщения? Декодирование – восстановление принятого сообщения из кодированного вида в вид доступный для потребителя. Что называется блочным кодированием? При блочном кодировании входная информация разбивается на блоки по k символов, которые преобразуются по определенному закону в n-символьные блоки, где n>k . Блочное кодирование предназначено, в основном, для обнаружения одиночных и групповых ошибок в канале связи и в определенных случаях для их исправления. Представьте пример реализации блочного кодирования при построении оптимального неравномерного кода. Кодируемые блоки располагаются в порядке убывания частот и двоичное кодирование осуществляется по тому же принципу. В ряде случаев разумно кодировать не на блоки букв, а целые куски текста. Например, «поздравляю новым годом желаю здоровья успехов в работе». |