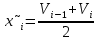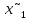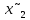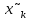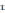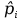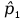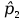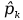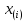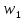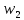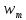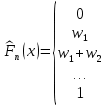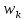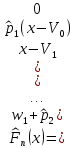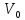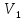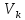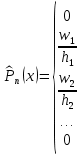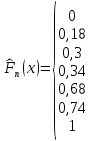Предварительная обработка выборочных данных. ЛР1. Отчет по лабораторной работе 1 Предварительная обработка выборочных данных
 Скачать 136.1 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Оренбургский государственный университет» Финансово-экономический факультет Кафедра математических методов и моделей в экономике Отчет по лабораторной работе №1 «Предварительная обработка выборочных данных» по дисциплине «Теория вероятностей и математическая статистика» ОГУ 38.03.01.6020.552 ОО Руководитель работы: ____________ «_____»_________________2020 г. Исполнитель: Студент гр. __________________ _________________ . «_____»_________________2020 г. Оренбург 2020 Теоретические сведения Выборочная совокупность представляет собой множество расположенных в беспорядке чисел; анализ таких данных затруднителен, поэтому необходима предварительная обработка данных. 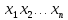 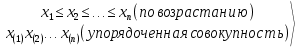- апостериорная выборка вариационный рядЕсли генеральная совокупность характеризуется дискретным признаком, то выборочную совокупность целесообразно представлять в виде дискретного вариационного ряда (ДВР). Таблица 1 – Показатели характеризующие ДВР
Если признак, характеризующий генеральную совокупность является непрерывным или дискретным, но принимающим большое количество возможных значений, то предварительная обработка выборочных данных сводится к построению интервального вариационного ряда (ИВР). 1. k- количество интервалов k=1+3,321*lgn; I- интервал 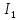 : [ 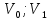) 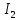: [ 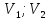)… 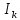 : [ 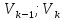]2. 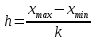 3. 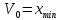 4. 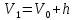 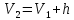 … 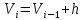 5. 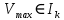 Таблица 2 – Показатели характеризующие ИВР
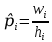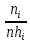 = Интервальный вариационный ряд строится таким образом, чтобы признак был более или менее распределен в каждом интервале. Этого удается достичь путем построения неравных интервалов. При использовании интервалов различной длины, анализ относительных и абсолютных частот становится некорректным, поскольку они зависят от длины интервала. В связи с этим вводится понятие плотности относительных частот, характеризующее число наблюдений, значений признака на единицу длины интервала. Оценка законов распределения генеральной совокупности Эмпирической функцией распределения 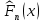 называется функция, которая для любого x определяется значением суммы относительных частот всех тех значений признака 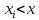 Таблица 3 – Построение эмпирической функции распределения для ДВР
Таблица 4 – Построение эмпирической функции распределения для ИВР
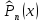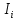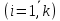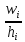Эмпирической плотностью распределения  называется функция, которая во всех интервалах   принимает значение  и равна 0 вне интервалов.Графиком эмпирической плотности распределения является гистограмма – фигура, состоящая из прямоугольников, основанием которых является величина интервалов, а высота – плотность относительных частот. ИВР:
Исходные данные
Ход решения Х1 Представим выборочные данные в виде ИВР: n=50 k=1+3,321*lg50 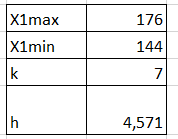 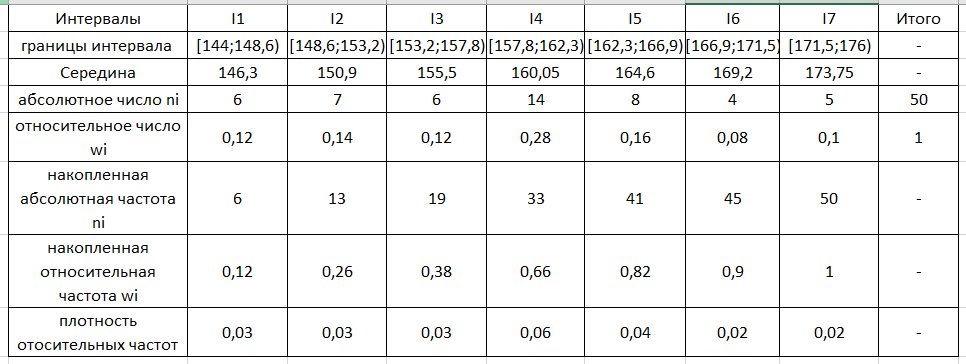 Построим оценку функции распределения: 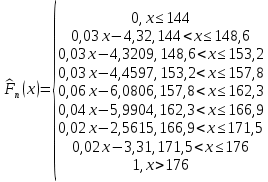 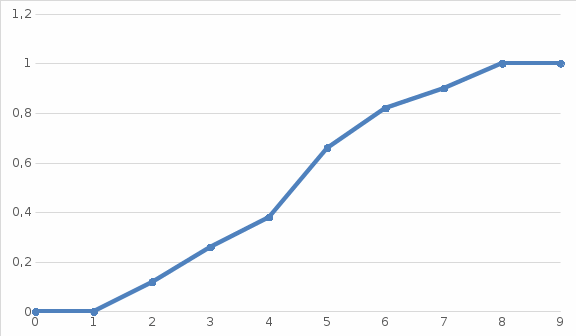 Рисунок 1 – Оценка функции распределения ИВР Построим оценку плотности распределения: 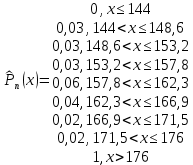 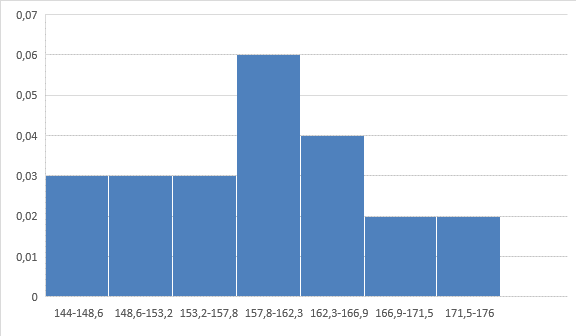 Рисунок 2 – Оценка плотности распределения ИВР Анализируя гистограмму, можно предположить, что генеральная совокупность распределена по нормальному закону распределения. Х4 Представим выборочные данные в виде ДВР: n=50 m=6  Построим оценку функции распределения:
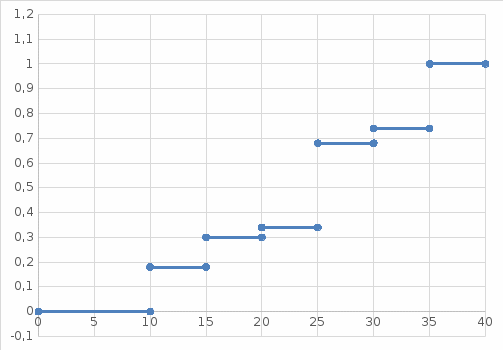 Рисунок 7 – Оценка функции распределения ДВР |
)
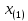
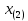
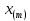
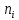
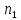
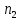
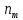
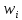
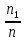
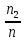
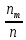
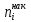
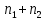
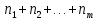
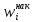
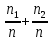
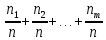
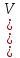