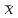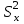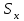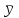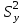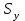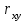Эконометрика Дмитриенко В.А ЛБ 1. Отчет по лабораторной работе 1 расчет точечных характеристик случайного вектора
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
 Федеральное агентство железнодорожного транспорта Федеральное агентство железнодорожного транспортаФедеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА АЛЕКСАНДРА I» Кафедра «Экономика и менеджмент в строительстве» Отчет по лабораторной работе № 1 «РАСЧЕТ ТОЧЕЧНЫХ ХАРАКТЕРИСТИК СЛУЧАЙНОГО ВЕКТОРА» Вариант 3
Санкт – Петербург 2021 Предмет изучения. Предметом изучения в лабораторной работе являются широко используемые математические соотношения для вычисления точечных числовых характеристик случайного вектора. 1.2. Цель работы. 1. Освоение математических соотношений для вычисления по табличным данным числовых характеристик экономических показателей. 2. Реализация вычислений точечных характеристик случайного вектора с помощью пакета стандартных программ на персональных ЭВМ. 3. Построение корреляционного поля случайной двумерной величины и изображение графика прямых линий, характеризующих выборочные средние значения каждой случайной величины. 1.3. Задание на лабораторную работу. Вычислить по выборке значений 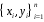 случайного вектора, представленных в таблице 1.1, числовые характеристики. Случайный вектор задан по 12 месяцам, он характеризует результирующий показатель –курс рубля и фактор – цена нефти. случайного вектора, представленных в таблице 1.1, числовые характеристики. Случайный вектор задан по 12 месяцам, он характеризует результирующий показатель –курс рубля и фактор – цена нефти.Таблица 1.1.
1.4. Краткие теоретические сведения По выборке значений 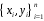 случайного вектора или случайной двумерной величины случайного вектора или случайной двумерной величины 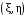 можно вычислить следующие оценки числовых характеристик генеральной совокупности: можно вычислить следующие оценки числовых характеристик генеральной совокупности: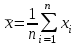 – выборочное среднее случайной величины – выборочное среднее случайной величины 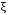 или выборочная оценка математического ожидания случайной величины или выборочная оценка математического ожидания случайной величины 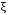 ; ;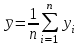 – выборочное среднее случайной величины – выборочное среднее случайной величины 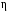 или выборочная оценка математического ожидания случайной величины или выборочная оценка математического ожидания случайной величины 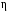 ; ;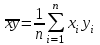 – выборочное среднее произведения случайных величин – выборочное среднее произведения случайных величин 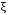 и и 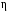 или выборочная оценка математического ожидания произведения случайных величин или выборочная оценка математического ожидания произведения случайных величин 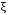 и и 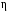 ; ;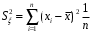 – выборочная дисперсия случайной величины – выборочная дисперсия случайной величины 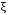 или выборочная оценка дисперсии случайной величины или выборочная оценка дисперсии случайной величины 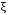 ; ;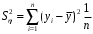 – выборочная дисперсия случайной величины – выборочная дисперсия случайной величины 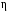 или выборочная оценка дисперсии случайной величины или выборочная оценка дисперсии случайной величины 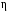 ; ;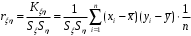 – выборочный коэффициент корреляции или выборочная оценка коэффициента корреляции случайных величин – выборочный коэффициент корреляции или выборочная оценка коэффициента корреляции случайных величин 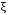 и и 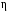 . Свойство оценки коэффициента корреляции: . Свойство оценки коэффициента корреляции: 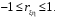 Для выборочных дисперсий 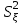 , , 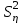 и выборочного корреляционного момента и выборочного корреляционного момента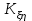 справедливы следующие соотношения: справедливы следующие соотношения: 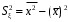 ; ; 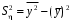 ; ; 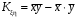 . .Приведенные соотношения для вычисления оценок числовых характеристик случайной величины и случайного вектора выступают в качестве точечных оценок параметров случайного вектора –курса рубля и импорта товаров. 1.5. Алгоритм и блок-схема алгоритма расчета точечных характеристик случайного вектора 1.5.1. Алгоритм расчета точечных характеристик компонент случайного вектора в Excel с помощью встроенных функций Расчет точечных оценок выполняется в среде Excel с помощью встроенных функций. Для их использования необходимо выбрать пустую ячейку и ввести в нее знак «=». Затем следует открыть список «Функции» и выбрать требуемую функцию. Если в этом списке она отсутствует, то ее можно найти, щелкнув по нижней строке списка «Другие функции…» (рис. 1.1). Так же вызов функции можно осуществить нажатием кнопки  – «Вставка функции», которая расположена слева от строки ввода формулы в ячейку. – «Вставка функции», которая расположена слева от строки ввода формулы в ячейку. Для расчета среднего выборочного значения технико-экономических показателей используется функция «СРЗНАЧ».     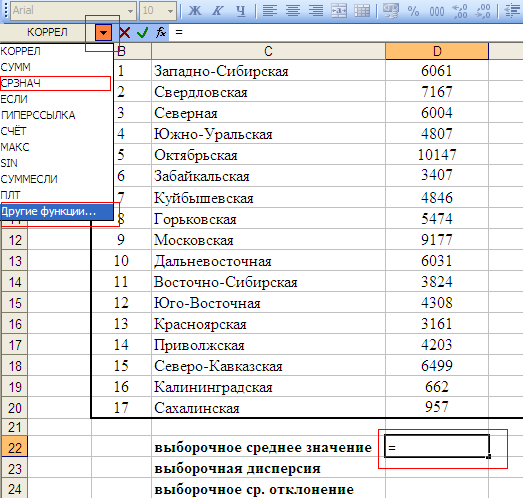 Рис. 1.1. Вызов списка встроенных функций Excel В качестве рабочей ячейки, для расчета среднего значения, удобно выбирать пустую ячейку непосредственно под столбцом статистических данных. После ввода знака «=» в эту ячейку, следует открыть список недавно используемых функций. Зачастую в этом списке присутствует искомая функция «СРЗНАЧ». В противном случае необходимо щелкнуть по строке «Другие функции…» (рис. 1.1). Выбор строки «Другие функции…» приведет к появлению на экране окна «Мастера функций». В верхней части этого окна можно ввести название искомой функции и нажать кнопку «Найти», либо выбрать категорию «Полный алфавитный перечень» и в перечне найти «СРЗНАЧ» (рис. 1.2).   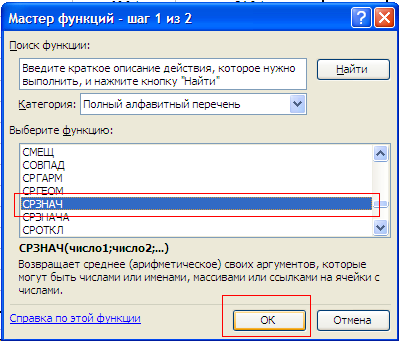 Рис. 1.2. Поиск функции «СРЗНАЧ» Подтверждение выбора функции «СРЗНАЧ» нажатием кнопки «ОК» приведет к появлению на экране окна «Аргументы функции». В верхней области для ввода данных задаются через двоеточие координаты первой и последней ячейки статистических данных (рис. 1.3).   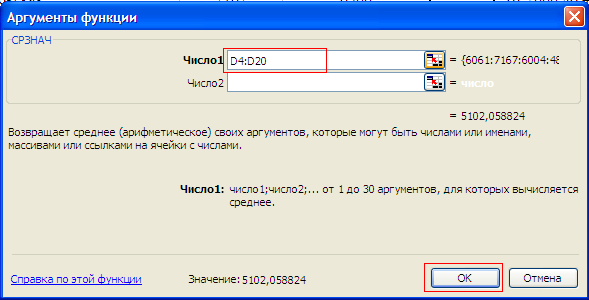 Рис. 1.3 Ввод аргументов функции «СРЗНАЧ» Кроме ввода данных через двоеточие, так же можно осуществлять эту процедуру с помощью выделения ячеек «протаскиванием» (после щелчка по соответствующей кнопке справа от области ввода данных). Реализация этого способа будет продемонстрирована ниже, в алгоритме расчета коэффициента корреляции. Заданный в строке «Число 1» диапазон статистических данных подтверждается нажатием кнопки «ОК». Как результат, в выбранной ячейке рабочего листа «Excel» появляется выборочное среднее значение оцениваемого экономического показателя (рис. 1.4). Если необходимо вычислить среднее значение еще одного экономического показателя по выборке той же самой размерности, то следует ввести новые данные в соседние ячейки (справа) и «протащить» вправо за правый нижний угол полученную формулу для расчета среднего значения (рис. 1.4).   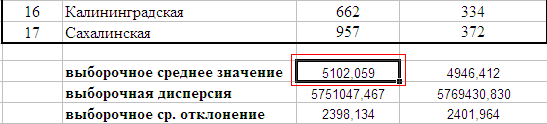 Рис. 1.4. Вывод результатов расчета выборочного среднего значения Аналогичным образом осуществляется вычисление других выборочных точечных оценок. Наименование встроенных функций Excel для расчета точечных оценок среднего, дисперсии и среднеквадратичного отклонения приведены в таблице 1.2. Таблица 1.2.
1.5.2. Алгоритм расчета выборочного коэффициента корреляции между двумя компонентами случайного вектора Расчет выборочного коэффициента корреляции осуществим в программе Excel с помощью встроенной функции «КОРРЕЛ». Для этого необходимо выделить пустую ячейку на рабочем листе «Лабораторная работа №1», и после нажатия клавиши «=» раскрыть список функций. Щелчок по строке «Другие функции» в списке функций приведет к появлению окна «Мастер функций». В нем необходимо выбрать категорию «Статистические» или категорию «Полный алфавитный перечень». После выделения функции «КОРРЕЛ» следует подтвердить выбор нажатием кнопки «ОК» (рис. 1.5). 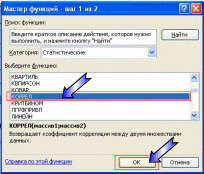 Рис. 1.5. Выбор функции «КОРРЕЛ» в списке статистических функций В окне для ввода аргументов необходимо задать массивы данных, для которых будет вычислено значение выборочного коэффициента корреляции. Ввод данных осуществляется щелчком по клавише ввода данных и последующим выбором диапазон данных для соответствующего массива. На рис. 1.6 и рис. 1.7 представлен ввод данных объясняющей переменной в поле «Массив1». Аналогичным образом вводятся данные результирующей переменной в поле «Массив2».  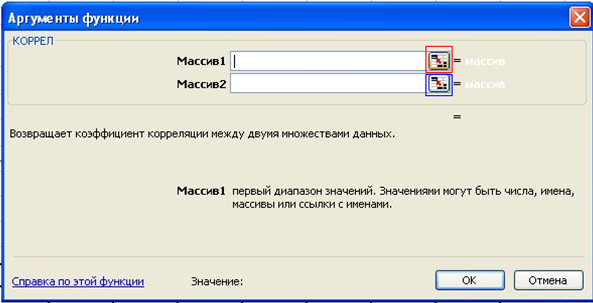 Рис. 1.6. Ввод данных объясняющей переменной   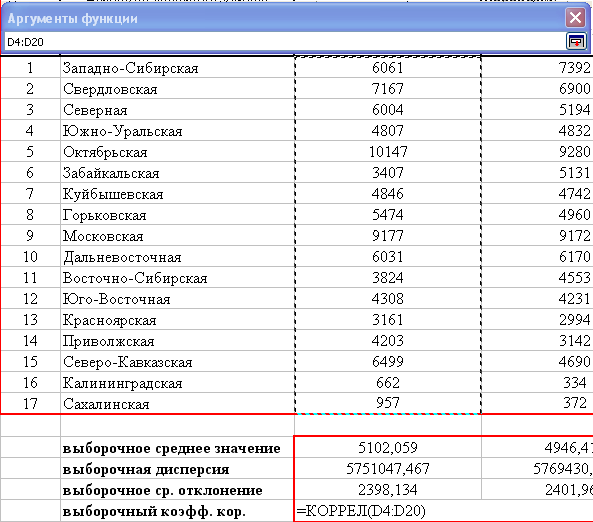 Рис. 1.7. Выбор диапазона данных объясняющей переменной Подтверждение диапазона данных в окнах «Массив1» и «Массив2» выполняется нажатием кнопки «ОК». Рассчитанное значение выборочного коэффициента корреляции появляется в выбранной ячейке (рис. 1.8).   Рис. 1.8. Вывод значения коэффициента корреляции в заданную ячейку Для построения корреляционного поля используются выборочные средние значения исследуемых показателей. На точечную диаграмму наносятся средние значения результирующей переменной на каждом уровне фактора. И, аналогично, наносятся средние значения фактора на каждом уровне результирующего показателя. Множества средних значений результирующего показателя соединяются гладкой линией. Множество средних значений фактора также соединяются гладкой линией. Результатом является график горизонтальной линии 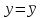 и вертикальной линии и вертикальной линии 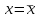 , на котором дополнительно отмечаются статистические данные в виде точек. , на котором дополнительно отмечаются статистические данные в виде точек.В случае расположения большего количества точек статистических данных в смежных областях корреляционного поля можно делать вывод о наличии линейной связи. Равномерное распределение статистических данных по различным областям корреляционного поля свидетельствует об отсутствии линейной связи между исследуемыми показателями. 1.5.3. Блок-схема алгоритма решения задачи математическими методами в электронных таблицах Excel На рис. 1.9. представлена блок-схема алгоритма по вычислению точечных характеристик случайного вектора в Excel с помощью встроенных функций «СРЗНАЧ», «ДИСПР», «СТАНДОТКЛОНП», «КОРРЕЛ».   Рис. 1.9. Блок-схема алгоритма по вычислению точечных оценок в Excel 1.6. Результаты расчетов точечных характеристик случайного вектора В таблице 1.3 приведены числовые характеристики исследуемых показателей, рассчитанные с помощью встроенных функций Excel «СРЗНАЧ», «ДИСПР», «СТАНДОТКЛОНП», «КОРРЕЛ», а на рис. 1.10 представлено корреляционное поле, построенное по средним значениям курса рубля и цены нефти. Таблица 1.3.
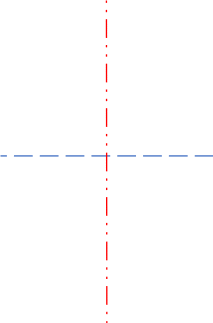 Рис. 1.10. Корреляционное поле технико-экономических показателей – курса рубля и цены нефти 1.7. Анализ полученных результатов Величина 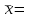 60,93 характеризует средний курс, вычисленный по 12 исследуемым месяцам. Среднее значение цены нефти составило 60,93 характеризует средний курс, вычисленный по 12 исследуемым месяцам. Среднее значение цены нефти составило 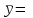 27,09. При этом разброс значений цены нефти и курса рубля относительно их средних составили соответственно 27,09. При этом разброс значений цены нефти и курса рубля относительно их средних составили соответственно 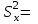 22,67 и 22,67 и 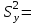 0,35. 0,35.Расчетное значение коэффициента корреляции 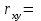 -0,11 близкое к 0 и расположение статистических данных в смежных областях корреляционного поля (рис. 1.10), свидетельствуют о наличии корреляционной связи между и ценой нефти и курсом рубля. Следовательно, имеет смысл осуществить построение парной линейной регрессии. -0,11 близкое к 0 и расположение статистических данных в смежных областях корреляционного поля (рис. 1.10), свидетельствуют о наличии корреляционной связи между и ценой нефти и курсом рубля. Следовательно, имеет смысл осуществить построение парной линейной регрессии. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||