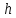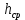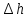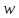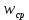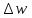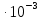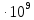отчет по 10 лр:модуль юнга. Отчет по лабораторной работе 10 Тема Определение модуля упругости (модуль Юнга) по деформации изгиба
 Скачать 407.57 Kb. Скачать 407.57 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ Кафедра общей и технической физики Отчет по ЛАБОРАТОРНОЙ РАБОТЕ № 10 Тема: «Определение модуля упругости (модуль Юнга) по деформации изгиба» Выполнил: студент гр. ВД-21 Аронович К.Ю. (шифр группы) (подпись) (Ф.И.О.) Проверил: руководитель работы: (должность) (подпись) (Ф.И.О.) Санкт-Петербург 2022 г Цель работы: Определить модуль Юнга материала путём измерения прогиба стержня при механической нагрузке. Краткое теоретическое содержание: Явление, изучаемое в работе: модуль упругости (модуль Юнга). Определение основных физических понятий, объектов, процессов и величин: Деформация – изменение размера и формы тема под действием сил. Деформация называется упругой, если она исчезает после прекращения действия сил. При упругой деформации, по закону, экспериментально установленному Гуком, величина абсолютной деформации Δl пропорциональна приложенной силе F: 𝐹 = 𝑘∆𝑙(1) Где k – постоянная величина для данного образца. Модуль Юнга – физическая величина, характеризующая способность материала сопротивляться растяжению, сжатию при упругой деформации. Механическое напряжение – отношение силы, приложенной к плоскости к площади этой плоскости. Измеряется в паскалях, единицах давления. Деформация изгиба – деформация, при которой одна из частей предмета сжимается, а другая растягивается. При этом плоскость, разделяющая верхнюю и нижнюю часть изгиба, находятся в ненапряженном состоянии. Законы и соотношения, описывающие изучаемые процессы, на основании которых получены расчётные формулы: Закон Гука при растяжении/сжатии стержня. где S – площадь поперечного сечения, [S] = м2; F – приложенная сила, [F] = Н; l –первоначальная длина тела, [l]= м; Δl – абсолютное удлинение стержня, [Δl] = м; E – коэффициент пропорциональности (модуль Юнга), [E] = Н/м2. Схема установки:  Рис 1. Экспериментальная установка и измеритель стрелы прогиба Установка (рис. 1) представляет собой стержень из исследуемого материала 1, расположенный горизонтально и своими концами свободно опирающийся на две призмы 2, обращенными рабочими ребрами вверх. Призмы установлены на вертикальных стойках поперечно по отношению к оси балки. Посередине стержня на него надета серьга 3, к которой подвешена платформа 4 с грузами 6. Стрела прогиба измеряется с помощью механического индикатора 5. Индикатор закреплен на общем основании с опорными стойками балки. 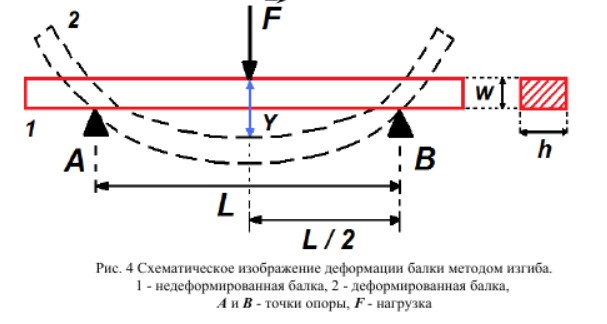 Рис 2. Схематическое изображение деформации балки методом изгиба. Где 1 – недеформированная балка; 2 – деформированная балка; А и В – точки опоры; F – нагрузка. Основные расчётные формулы Определение модуля Юнга 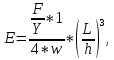 [Н/м2] или [Па], где F – приложенная в центре стержня сила [Н]; w и h – размеры поперечного сечения стержня [м]; Y – стрела прогиба стержня под нагрузкой; L – расстояние между опорами балки [м]. [Н/м2] или [Па], где F – приложенная в центре стержня сила [Н]; w и h – размеры поперечного сечения стержня [м]; Y – стрела прогиба стержня под нагрузкой; L – расстояние между опорами балки [м]. Расчёт силы тяжести 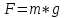 , [Н], где m – масса груза [кг]; g – ускорение свободного падения = 9,8 [м/с2]. , [Н], где m – масса груза [кг]; g – ускорение свободного падения = 9,8 [м/с2].Расчёт стрелы прогиба 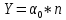 , [м], где , [м], где 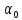 – цена деления индикатора; n – отсчёт по шкале индикатора прогиба. – цена деления индикатора; n – отсчёт по шкале индикатора прогиба.Погрешности прямых измерений 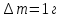 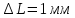 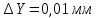 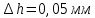 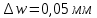 Формула для расчёта погрешностей косвенных измерений 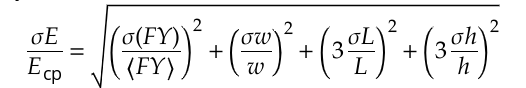 Таблицы с результатами измерений и вычислений Табл. 1. Результаты измерений и расчётов
Табл. 2. Результаты измерений и расчётов
Пример вычисления для опыта №1 Исходные данные: L = 420 мм = 0,42 м Вычисления: Расчёт средних значений высоты и ширины поперечного сечения стержня: 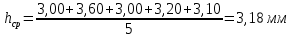 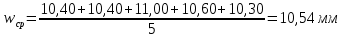 Расчет силы, действующей на балку: 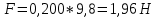 Стрела прогиба балки: 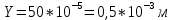 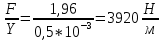 Модуль Юнга: 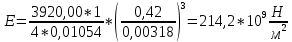 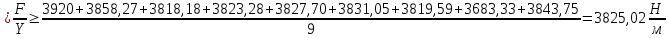 Погрешность косвенных измерений: 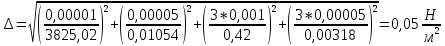 Среднее значение модуля Юнга: 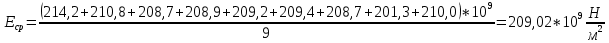 Окончательный результат: 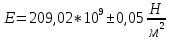 Графический материал 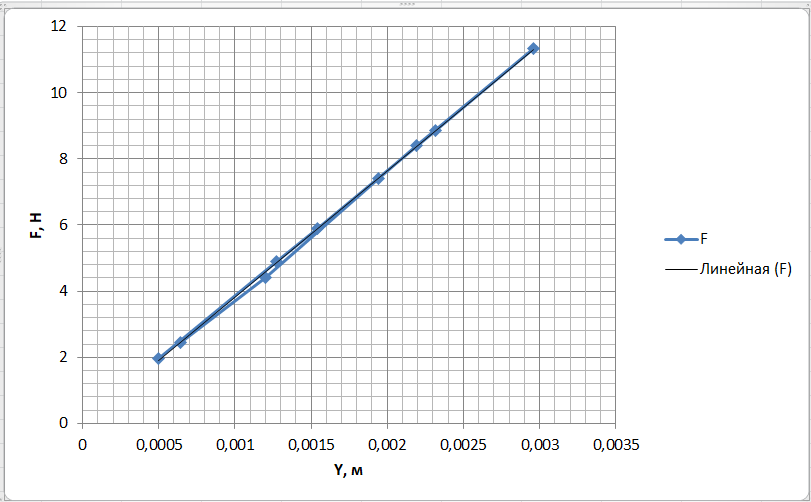 Рис. 3. Зависимость прогиба стержня от силы тяжести, действующей на стержень. Вывод Модуль Юнга равен 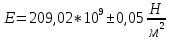 . Это говорит о том, что материал, из которого сделан стержень, - никель. . Это говорит о том, что материал, из которого сделан стержень, - никель. Из графика следует, что величина прогиба для двух циклов (увеличения и уменьшения массы грузов) примерно одинакова под действием одинаковых сил. |