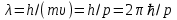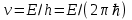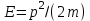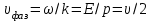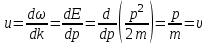отчет Дифракция электронов. oтчет лаб 12. Отчет по лабораторной работе 12 "Дифракция электронов"
 Скачать 233.98 Kb. Скачать 233.98 Kb.
|
|
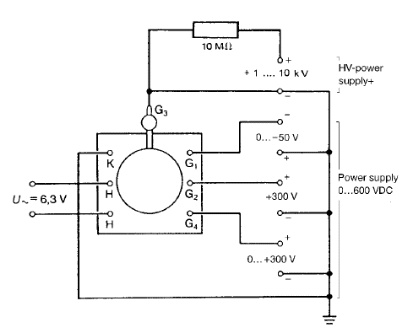
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО науки и высшего ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» ОТЧЕТ По лабораторной работе № 12 “Дифракция электронов” Выполнил: студент гр. НБШ-22 /Ле Нгуен Туан Ха / (шифр группы) (подпись) (Ф.И.О.) Дата: Проверил: (должность) (подпись) (Ф.И.О.) Санкт-Петербург 2023 Теоретическое содержание. Цель работы: Исследование волновых свойств электронов Явление изучаемое в работе: Дифракционный метод  3 Схему установки:
Физическое обоснование цели работы и метода измерения: При исследовании теплового излучения абсолютно чёрного тела и явления фотоэффекта было установлено, что испускание и поглощение излучения происходит отдельными порциями (квантами), причём энергия кванта излучения равна E = hnили в другой записи: E = ħw, (1) где w=2pn — угловая частота соответствующего электромагнитного излучения, а ħ = h/2p— модифицированная постоянная Планка ( 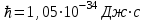 ). ).Квант электромагнитного излучения, или фотон как частица (корпускула) особого рода, не имеющая массы покоя, обладает энергией (1) и импульсом: 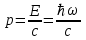 (2) (2)Кроме того, исходя из общего соотношения между массой и энергией 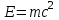 , ,фотону можно также приписать некоторую величину, по размерности совпадающую с массой (не следует, смешивать это понятие с понятием массы в классической механике): 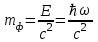 , (3) , (3)где с — скорость света в вакууме. Итак, было установлено, что свет (излучение) обладает как волновыми, так и корпускулярными свойствами. Впервые гипотезу о волновых свойствах электрона высказал в 1925 г. французский физик Луи де Бройль1. Основная мысль де Бройля сводилась к тому, что можно применить квантовую теорию света для описания волновых свойств, движущихся элементарных частиц. При этом он предположил, что движущийся свободный электрон, имеющий импульс  и кинетическую энергию Е, описывается такой же функцией, что и плоская волна: и кинетическую энергию Е, описывается такой же функцией, что и плоская волна: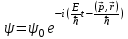 , (4) , (4)где скалярное произведение 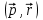 равно: равно: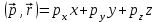 , (5) , (5)а 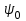 — постоянная амплитуда. — постоянная амплитуда.По аналогии с квантовой теорией света де Бройль предположил, что соотношения (1) и (2), определяющие энергию и импульс фотона, справедливы и для волны, сопоставляемой свободному электрону, т.е. частота w такой волны и волновое число k определяются формулами: 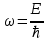 ; (6) ; (6)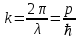 . (7) . (7)Отсюда с учетом (6) и (7) выражение для обычной плоской электромагнитной волны: 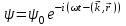 , ,принимает вид (4), т.е. получаем плоскую волну, названную позже волной деБройля. В более простом случае движения свободного электрона вдоль оси ОХ соответствующая (4) волновая функция будет иметь вид: 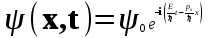 . (8) . (8)В 1927 г. гипотеза де Бройля была подтверждена опытами по дифракции электронов, а еще позже на опыте были установлены волновые свойства и других элементарных частиц. Поэтому можно сказать, что электрону, движущемуся со скоростью 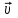 , при условии, что , при условии, что 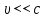 , будет соответствовать длина волны: , будет соответствовать длина волны: , (9) , (9)называемая длиной волны деБройля. Распространение волн де Бройля не связано с распространением в пространстве электромагнитного поля. Волны де Бройля имеют специфическую квантовую природу, не имеющую аналогов в классической физике. Движущаяся частица обладает кинетической энергией:  . .Так как модуль импульса равен 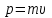 , то можно записать выражение кинетической энергии через модуль импульса: , то можно записать выражение кинетической энергии через модуль импульса: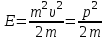 , ,а модуль импульса выразить через кинетическую энергию: 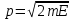 . .Тогда соотношение (9) можно представить в виде: 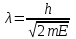 . .Для электрона, ускоренного электрическим полем с разностью потенциалов U (или  ), кинетическая энергия может быть выражена через разность потенциалов и заряд: ), кинетическая энергия может быть выражена через разность потенциалов и заряд: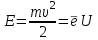 , ,где 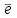 — заряд электрона. — заряд электрона. . (10) . (10)  Рис. 1. В 1927 году Дэвиссон и Джермер подтвердили экспериментально гипотезу де Бройля, исследуя отражение электронов от монокристалла никеля, принадлежащего кубической системе. Кристалл был отшлифован перпендикулярно диагонали кристаллической ячейки (111) (рис. 1). Пучок электронов падал на отшлифованную грань. Изменялись интенсивность электронного пучка и угол 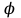 . На пути отражённого электронного пучка был расположен цилиндрический электрод (Э). Интенсивность отражённого пучка оценивалась по силе тока, текущего через гальванометр. Рассеяние оказалось особенно интенсивным при определённом угле . На пути отражённого электронного пучка был расположен цилиндрический электрод (Э). Интенсивность отражённого пучка оценивалась по силе тока, текущего через гальванометр. Рассеяние оказалось особенно интенсивным при определённом угле 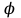 , который соответствовал отражению от атомных плоскостей. Сила тока оказалась значительной при напряжении 54 В. Длина волны Брэгга была вычислена по формуле , который соответствовал отражению от атомных плоскостей. Сила тока оказалась значительной при напряжении 54 В. Длина волны Брэгга была вычислена по формуле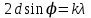 , (11) , (11)где d — расстояние междуатомными плоскостями и получилась равной 1,65*10-10 м. Вычисления по формуле (9) дали длину волны 1,67*10-10 м. Это послужило экспериментальным доказательством гипотезы де Бройля. Аналогично тому, как согласуются между собой квантовая и волновая теории света, согласуются корпускулярные и волновые свойства элементарных частиц, в частности электронов. Пусть число электронов (или других частиц), попавших в данный элемент объёма dV, пропорционально квадрату амплитуды волны де Бройля и величине элемента объема, т. е. число электронов приблизительно равно  . Тогда вероятность dW того, что частица находится в данном элементе объема dV, пропорциональна квадрату амплитуды волны де Бройля, или квадрату модуля этой волны, т.е.: . Тогда вероятность dW того, что частица находится в данном элементе объема dV, пропорциональна квадрату амплитуды волны де Бройля, или квадрату модуля этой волны, т.е.: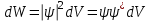 , (12) , (12)где 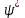 — функция, комплексно сопряжённая с самой волновой функцией. Из этого равенства следует, что квадрат модуля волны де Бройля (волновой функции) равен плотности вероятности нахождения свободной частицы в данной точке пространства. Такое толкование волновой функции справедливо не только для свободного электрона, но и для связанного электрона. Волновая функция удовлетворяет условию нормировки вероятностей: — функция, комплексно сопряжённая с самой волновой функцией. Из этого равенства следует, что квадрат модуля волны де Бройля (волновой функции) равен плотности вероятности нахождения свободной частицы в данной точке пространства. Такое толкование волновой функции справедливо не только для свободного электрона, но и для связанного электрона. Волновая функция удовлетворяет условию нормировки вероятностей: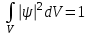 , ,это означает, что пребывание частицы где-либо в пространстве, есть достоверное событие и вероятность этого события равна 1. Следовательно, физический смысл волновой функции состоит в том, что квадрат её модуля есть плотность вероятности обнаружить частицу (электрон) в данной точке пространства, причем сама волновая функция является комплексной величиной. По поводу волновых свойств электрона необходимо заметить также, что с точки зрения квантовой теории движение электронов можно рассматривать как электронные волны, определяемые волновыми функциями Y. Хотя сама волновая функция не имеет особого физического смысла, однако для свободного электрона существует определенная и весьма наглядная связь движения волны с движением самого электрона. В самом деле, если рассматривать не строго монохроматическую волну с определёнными величинами w и 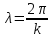 , а почти монохроматическую волну или группу волн (пакет), то: , а почти монохроматическую волну или группу волн (пакет), то: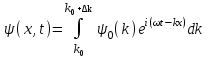 , ,где ko — есть волновое число, соответствующее середине группы. Известно, что групповая скорость vгр или скорость группы волн vопределяется формулой: 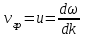 . .С другой стороны, для свободного электрона из (6) и (7) имеем: 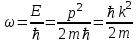 . .Тогда, на основании последнего выражения, скорость группы волн, или скорость пакета, будет равна: 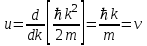 , ,где v — есть модуль мгновенной скорости свободного электрона. Связь между корпускулярными и волновыми свойствами частиц, обладающих массой покоя m, отражена в таблице 1. Таким образом, для простейшего случая свободного электрона можно заключить, что групповая скорость волн де Бройля равна скорости движения электрона (частицы). Таблица 1
В этом смысле можно сказать, что волновая функция для свободного электрона или волна де Бройля имеет наглядное физическое истолкование. Поэтому с известным приближением движение свободного электрона можно рассматривать как движение группы (пакета) волн де Бройля. В отличие от электромагнитных волн для волн де Бройля существует дисперсия даже для частицы в вакууме.  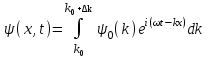 , ,где ko — есть волновое число, соответствующее середине группы. Известно, что групповая скорость vгр или скорость группы волн vопределяется формулой: 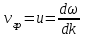 . .С другой стороны, для свободного электрона имеем: 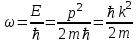 . .Тогда, на основании последнего выражения, скорость группы волн, или скорость пакета, будет равна: 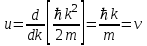 , ,где v — есть модуль мгновенной скорости свободного электрона. Приборные погрешности: ∆Dвнут = ∆Dвнеш = 1мм ∆UA = 0.1кВ Результаты прямых измерений и вычислений:
Длина волны рассчитывается из анодного напряжения Для определения диаметра дифракционного кольца, измерьте внутренний и внешний край кольца штангенциркулем (в затемненной комнате). Найдите середину ширины кольца: отнимите от внешнего диаметра кольцаDвн внутреннийDвнут: ∆D = Dвн - Dвнут разницу разделите пополам. Для нахождения радиуса кольца r прибавьте к диаметру внутреннего края кольца Dвнут половину ширины кольца ∆D /2 и разделите пополам. r = (∆D/2 + Dвнут)/2. в соответствии с 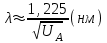 , результаты расчётов занесите в таблицу: , результаты расчётов занесите в таблицу:
погрешности измерений межплоскостных расстояний графита Δ d1 и Δ d2 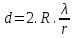
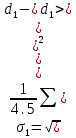 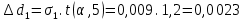 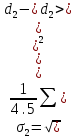 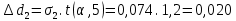 Окончательный результат: 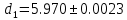 мм мм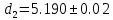 мм мм r (мм) Построенные графики зависимостей  : :   r1 r2 λ, (пм) 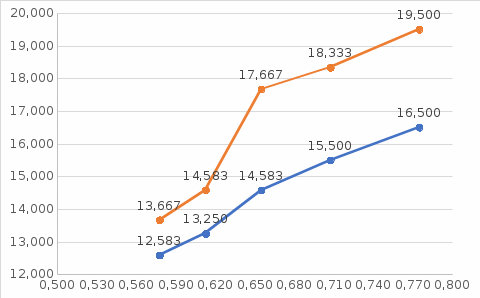 Вывод Опытным путем мы получили, что при электромагнитной дифракции диаметр дифракционного кольца пропорционален электрическому току. 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||