ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ГАЗА МЕТОДОМ НАГРЕТОЙ НИТИ. лаба 17. Отчет по лабораторной работе 17 определение коэффициента теплопроводности газа методом нагретой нити
 Скачать 236.12 Kb. Скачать 236.12 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра общей и технической физики ОТЧЕТ по лабораторной работе № 17 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ГАЗА МЕТОДОМ НАГРЕТОЙ НИТИ Автор: студент гр. (Шифр группы) (подпись) (ФИО) Дата: Проверил: (подпись) (ФИО) Санкт-Петербург 2022 ЦЕЛЬ РАБОТЫ определить коэффициент теплопроводности воздуха методом нагретой нити при атмосферном давлении и различных температурах поверхности вертикальной цилиндрической трубки КРАТКОЕ ТЕОРЕТИЧЕСКОЕ СОДЕРЖАНИЕ Явление, изучаемое в работе: явление переноса энергии между молекулами газов (явление теплопроводности) Нарушение равновесия приводит к переносу из одних мест среды в другие вещества (диффузия), импульса (вязкость), энергии или тепла (теплопроводность). Эти явления носят название явлений переноса. Интенсивность процесса характеризуется потоком той или иной величины. Поток любой физической величины - это её количество, переносимое в единицу времени через воображаемую поверхность, перпендикулярно направлению переноса. Плотностью потока физической величины называется ее количество, переносимое в единицу времени через единичную площадку, перпендикулярно направлению переноса. Коэффициент теплопроводности - физическая величина, характеризующая и численно равная плотности потока энергии при градиенте температуры равном единице. Закон теплопроводности Фурье: вектор плотности теплового потока, передаваемого теплопроводностью, пропорционален вектору градиента температуры 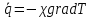 , ,где χ – коэффициент теплопроводности, gradT – градиент температуры. Метод нагретой нити. Метод применяется для изучения процессов теплообмена в лабораторных условиях. Нить представляет собой проволоку, натянутую вдоль оси вертикального цилиндра. Нить цилиндра нагревается электрическим током I. После того как устанавливается стационарный режим, температура нити перестанет изменяться. Выделяющееся при этом тепло полностью отдается в окружающую среду. Закон Джоуля-Ленца: количество тепла, выделившегося в проводнике при прохождении по нему тока, определяется по формуле 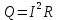 , ,гдеQ – поток тепла, I – сила тока, R – сопротивление Сопротивление нити: 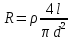 , ,где ρ, l, d – удельное сопротивление, длина и диаметр нити Зависимость электрического сопротивления от температуры: 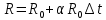 , , где 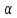 – коэффициент температурного сопротивления, – коэффициент температурного сопротивления, 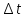 – разность температур у поверхностей проволоки Tr и цилиндра TR – разность температур у поверхностей проволоки Tr и цилиндра TRОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ Поток тепла, переносимый воздухом с проволоки: 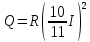 , ,где Q – поток тепла, [Q] = Вт, R – сопротивление, [R] = Ом, I – сила тока, [I] = А. Температура поверхности проволоки: 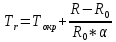 , ,где Tокр – температура окружающей среды (воздуха), [Tокр] = К, R – сопротивление, [R] = Ом, R0 – сопротивление проволоки при комнатной температуре, [R0] = Ом, 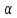 – коэффициент температурного сопротивления, – коэффициент температурного сопротивления, 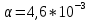 Ом/град. Ом/град.Коэффициент теплопроводности: 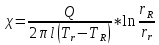 , ,гдеQ – поток тепла, [Q] = Вт, l – длина цилиндра, [l] = м, Tr– температура газа у поверхности цилиндра, [Tr] = К, TR – температура газа у поверхности нити, [TR] = К, rR– радиус цилиндра, [rR] = м, rr– радиус нити, [rr] = м, 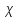 – коэффициент теплопроводности, [ – коэффициент теплопроводности, [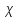 ] = ] = 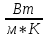 . .СХЕМА УСТАНОВКИ 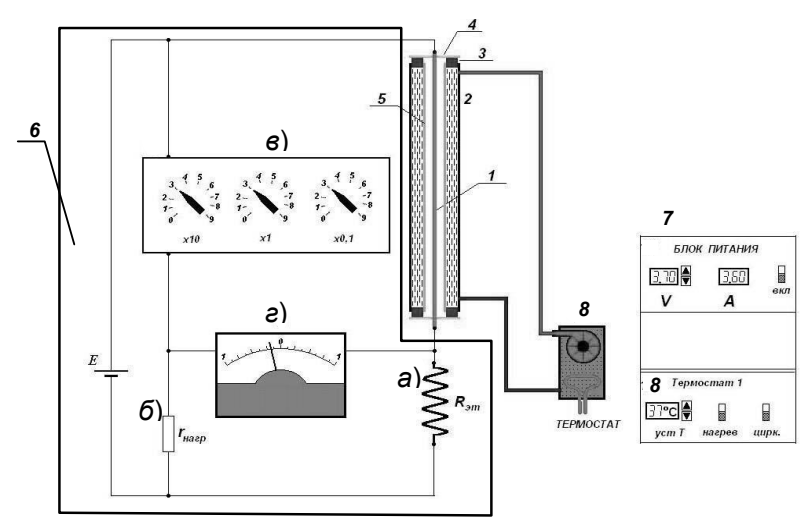 Вертикальная цилиндрическая трубка длиной l с двойными стенками и с натянутой внутри проволокой; магазин сопротивлений; эталонное Rэт = 3,5 Ом и нагрузочное rн = 35 Ом сопротивление; гальванометр; источник питания; термостат. Нить 1 (проволока) натянута между упорами 3, 4 внутри трубки 2. Трубка 5 имеет двойные стенки, между которыми циркулирует вода с заданной температурой. Температура стенок трубки поддерживается термостатом 8, который управляется с пульта управления с надписью "8 термостат 1". Нить 1 включена в схему измерительного моста Уинстона 6, состоящего из эталонного а) и нагрузочного б) сопротивлений, магазина сопротивлений в) и гальванометра г). Параметры моста подобраны таким образом, что при балансе моста сопротивление магазина сопротивлений в 10 раз больше сопротивления нити. Вся схема подключена к источнику питания Е, параметры которого задаются с пульта 7. ФОРМУЛЫ ДЛЯ РАСЧЕТА ПОГРЕШНОСТЕЙ КОСВЕННЫХ ИЗМЕРЕНИЙ Коэффициент теплопроводности: 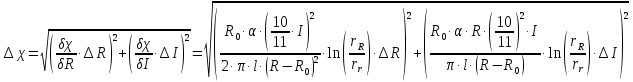 , ,гдеR – значение результата измерения сопротивления, [R] = Ом, 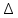 R – приборная погрешность сопротивления, [ R – приборная погрешность сопротивления, [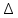 R] = Ом, R] = Ом,R0 – сопротивление проволоки при комнатной температуре, [R0] = Ом, I – значение результата измерения силы тока, [I] = А, 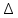 I – приборная погрешность силы тока, [ I – приборная погрешность силы тока, [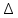 I] = А, I] = А,l = 0,5 м – длина проволоки, α = 4,6*10-3 Ом/град – коэффициент температурного коэффициента, rr = 5*10-5 м – радиус проволоки, rR = 4*10-3 м – радиус внутренней стенки цилиндра. Исходные данные: l = 0,5 м – длина проволоки, α = 4,6*10-3 Ом/град – коэффициент температурного коэффициента, rr = 5*10-5 м – радиус проволоки, rR = 4*10-3 м – радиус внутренней стенки цилиндра. Tокр = 293 K Погрешности прямых измерений: 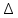 R= 0,05 Ом, R= 0,05 Ом,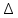 I= 0,01 А, I= 0,01 А, 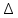 T= 1 К. T= 1 К.Результаты измерений
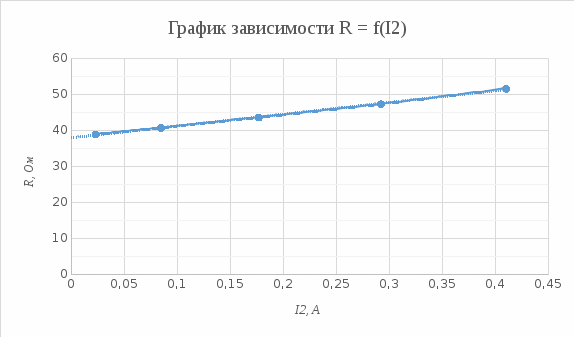 R0 = 38 Ом – сопротивление проволоки при комнатной температуре Результаты измерений и вычислений зависимости сопротивления проволоки от протекающего тока
ПРИМЕР РАСЧЕТА: Поток тепла: 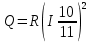 = 38,8*(0,15 * 10/11) 2 = 0,72 Вт = 38,8*(0,15 * 10/11) 2 = 0,72 ВтТемпература поверхности проволоки: 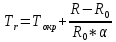 = 293,15+(38,8-- 38) / (38 * 4,6 * 10-3) = 297,73 К = 293,15+(38,8-- 38) / (38 * 4,6 * 10-3) = 297,73 КСреднеарифметическая температура: 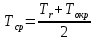 = (297,73 + 293,15) / 2 = 295,44 К = (297,73 + 293,15) / 2 = 295,44 ККоэффициент теплопроводности: 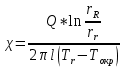 = == 0,72 * ln (4*10-3 / 5*10-5) / (2 * 3,14 * 0,5 * (297,73-293,15)) = 0,22 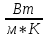 Погрешность коэффициента теплопроводности: 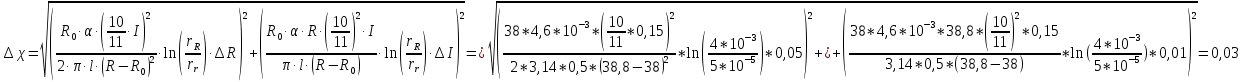 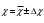 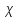 = (0,33±0,03) = (0,33±0,03) 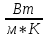 для 20℃ для 20℃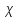 = (0,29±0,01) = (0,29±0,01) 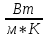 для 40℃ для 40℃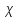 = (0,262±0,006) = (0,262±0,006) 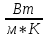 для 60℃ для 60℃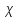 = (0,245±0,004) = (0,245±0,004) 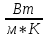 для 80℃ для 80℃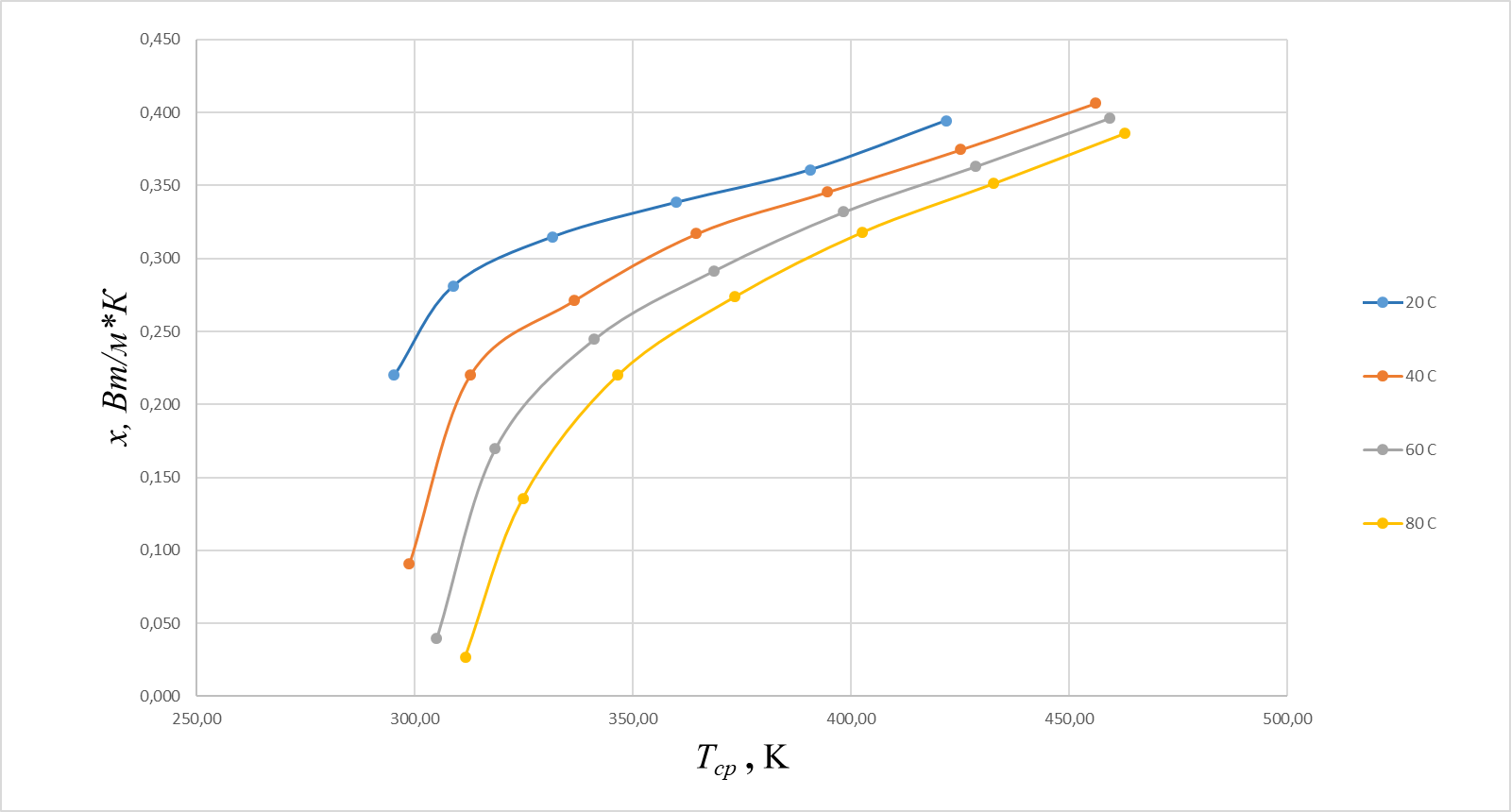 ВЫВОД В данной лабораторной работе был экспериментально определён коэффициент теплопроводности воздуха, который оказался равен 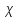 = (0,33±0,03) = (0,33±0,03) 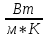 . Полученный результат отличается от справочного значения, равного 0,026 . Полученный результат отличается от справочного значения, равного 0,026 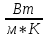 , на , на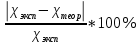 = = 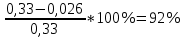 . Можно утверждать о неточности данной методики и о грубых ошибках в измерениях. . Можно утверждать о неточности данной методики и о грубых ошибках в измерениях. |
