Отчет по лабораторной работе 2 Тема Дискретнособытийная модель работы банковского отделения
 Скачать 1.52 Mb.
|
|
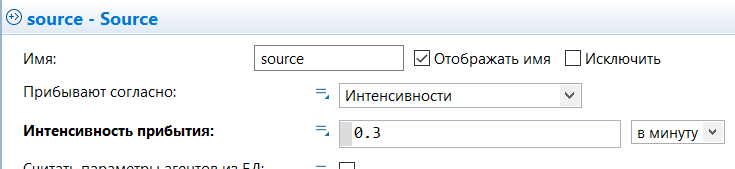
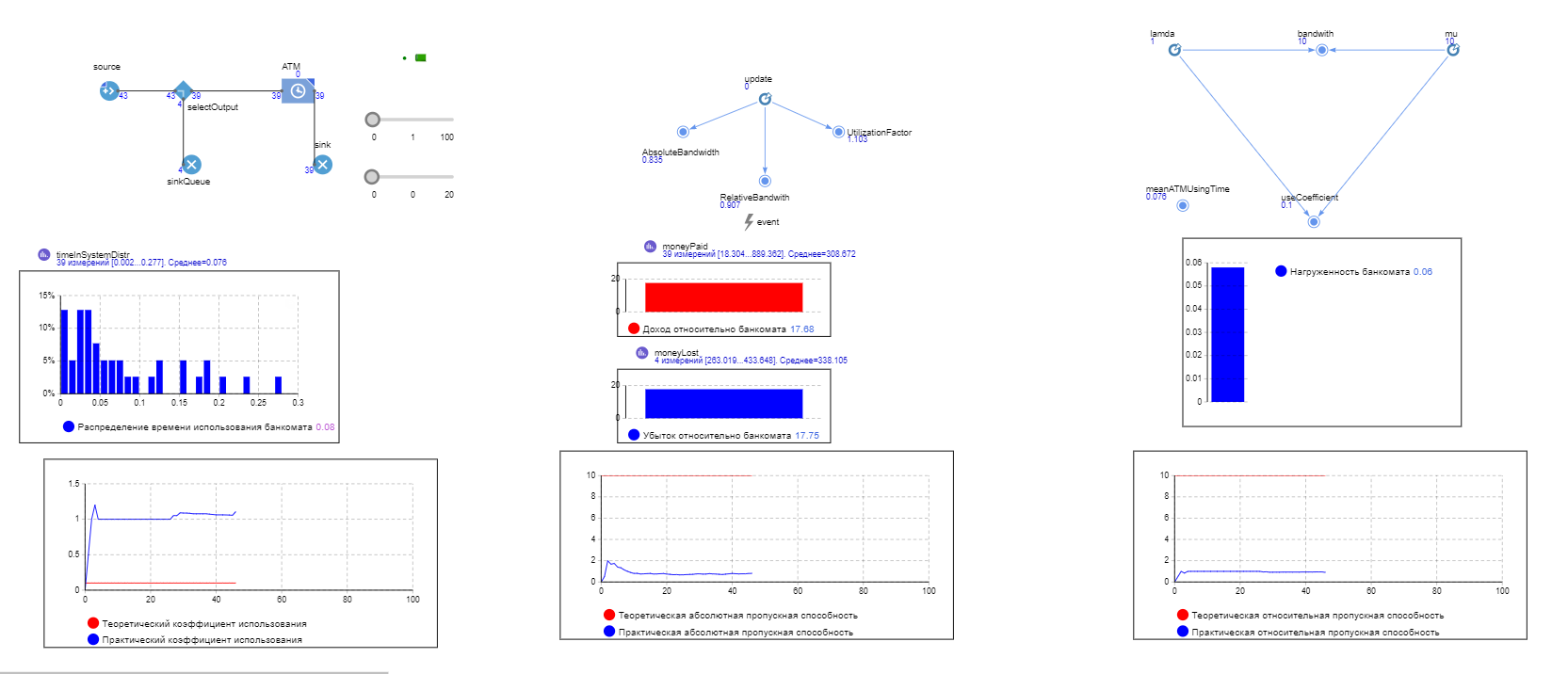
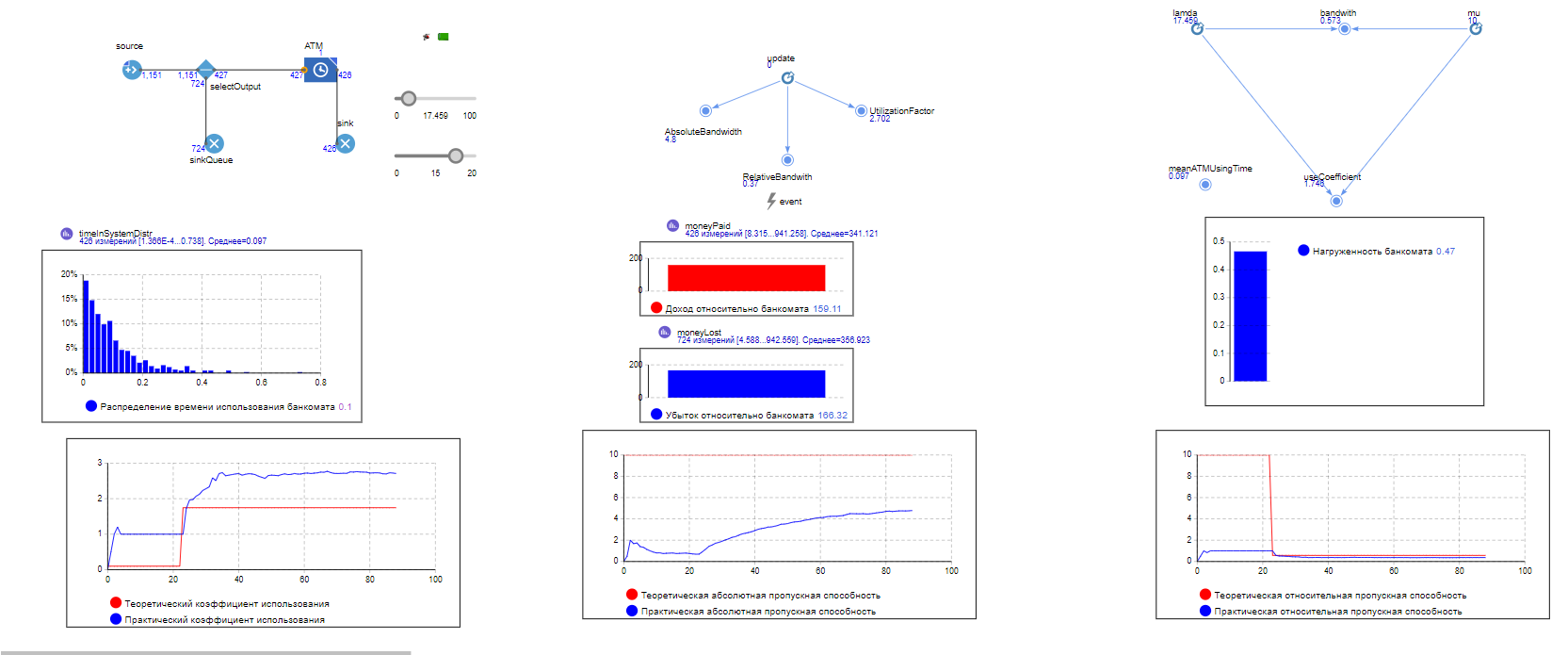
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Ф  акультет Информационных Систем и ТехнологийК  афедра «Информационные системы»Д  исциплина «Методы моделирования»ОТЧЕТ по лабораторной работе №2 Тема Дискретно-событийная модель работы банковского отделения   Выполнил студент ___________________ /______А.Р. Шадаев_____/ подпись инициалы, фамилия К  урс 3 Группа ПИбд-32 Направление/ специальность 09.03.04 Программная инженерия_______________ Р  уководитель доцент, к.т.н., Евсеева Ольга Николаевнадолжность, ученая степень, ученое звание _______________________________________________________________________ фамилия, имя, отчество Дата сдачи: «____»_________________20____г. Дата защиты: «____»________________20____г. Оценка: ______________________ Ульяновск 2023 г. Задание 1:Постройте модель СМО М/М/1/1. Интенсивность входного потока lamda и интенсивность обслуживания mu для которой задаются интерактивно. Определите ее показатели эффективности в теории (расчет) и на практике (модель). Сравните свои результаты. Создадим агент Customer, в нем определим 3 параметра: 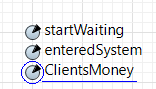 startWaiting – отвечает за ожидание клиентом освобождения банкомата. Значение не указано, потому что параметр будет инициализировать в ходе работы программы. enteredSystem – отвечает за начало отсчета времени клиентом за банкоматом. Значение не указано, потому что параметр будет инициализировать в ходе работы программы. ClientsMoney – отвечает за финансовые средства клиента, по умолчанию равен 10. Также в агенте Customer находится 3d-модель клиента. А в агенте Teller находится только 3-d модель офисного работника. Вернемся к агенту Main. Сделаем 3-d модель банкомата и окно, где будет моделироваться ситуация обслуживания клиента у банкомата.  В свойствах цвета точечного узла пропишем следующее:  То есть, если банкомат свободен, то точка будет отмечена зеленым цветом, в противном случае – красным. Создадим окно 3-d моделирования: 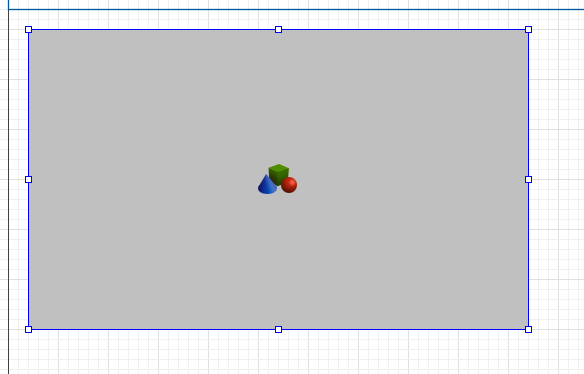 Чтобы построить такую систему массового обслуживания, нам нужно построить следующую схему:  source – генерирует агентов (в нашем случае посетителей банка); selectOutput – развилка if-else. Если банкомат (ATM) никого не обслуживает (ATM.size < 1, т.е. его вместимость равна 0), то клиент переходит к банкомату. В противном случае клиент переходит в блок sinkQueue, где объект клиента будет уничтожен;  sinkQueue – уничтожает поступивших клиентов. В этом блоке также ведется статистика и передается на график - когда клиент входит в этот блок, в данные гистограммы moneyLost будет записываться информация о том, сколько мы бы могли заработать денег, но из-за того, что банкомат уже был в это время занят, а значит клиент не смог воспользоваться банкоматом, поэтому мы не смогли заработать деньги клиента, а значит для нас эти деньги будут считаться потерянными. Как раз на графике будет отсчитываться этот убыток относительно банкомата;   - отвечает за убыток относительно банкомата ATM – банкомат. Представляет из себя блок Delay. В нашем случае задерживает клиентов на заданный период времени. Это означает, что клиент тратит время на проведение необходимой ему операции у банкомата ATM; ATM вмещает в себя только одного клиента. Моделирует время задержки с помощью функции exponential(mu, 0) в минуту, которая генерирует экземпляр экспоненциального распределения. Экспоненциальное распределение часто используется для того, чтобы смоделировать время между случайными событиями, например, время между прибытиями поездов в модели очередей. В качестве 1-го параметра принимает параметр формы распределения, а 2-го – минимальное значение переменной. В нашем случае 1-й параметр – параметр mu, а 2-й – нулевое значение. Параметр mu представляет из себя интенсивность обслуживания клиентов. Численно равен 10.   Обязательно должна быть установлена галочка напротив пункта «Включать сбор статистики» для дальнейшего анализа информации по обслуживанию клиентов у банкомата.  При входе в блок ATM обязательно считается то, сколько времени у банкомата провел клиент. 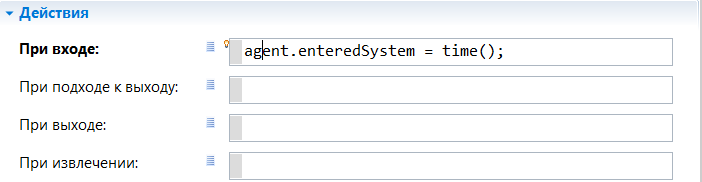 sink – уничтожает поступивших клиентов. В отличие от блока sinkQueue считает сколько времени у банкомата провел клиент путем добавления информации о проведенном времени в данные гистограммы timeInSystemDistr и в дальнейшем отображения этих данных на графике. Также подсчитывает сколько денег внес клиент в банкомат путем добавления информации о деньгах клиента в данные гистограммы moneyPaid, также эта информация будет отображена на графике.  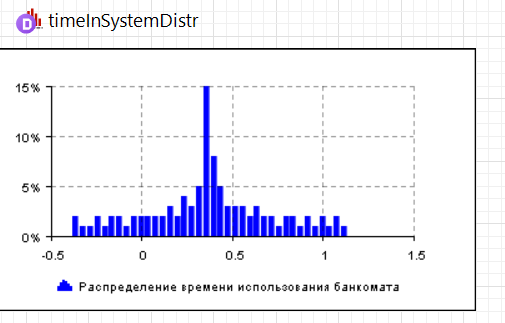 - отвечает за распределение времени при использовании банкомата  - отвечает за полученный доход от клиента относительно банкомата Вся схема:  Значения lamda и mu будем задавать с помощью следующей схемы:  lamda - интенсивность входящего потока. 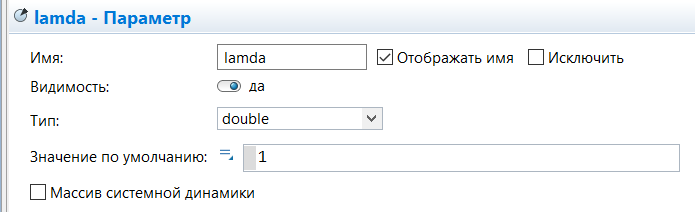 mu – интенсивность обсдуживания. Он же и является по определению абсолютной пропускной способностью.  bandwith – относительная пропускная способность. Ее значение определяется путем деления mu на lamda (mu/lamda) 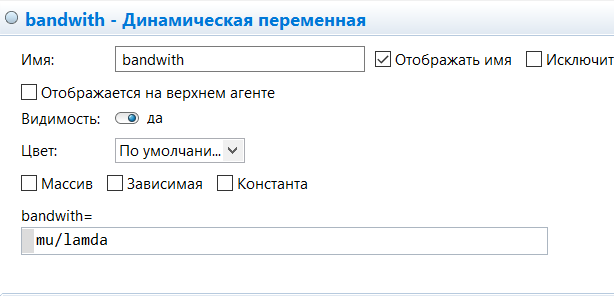 useCoefficient – коэффициент использования. Значение параметра определяется путем деления lamda на mu (lamda/mu) 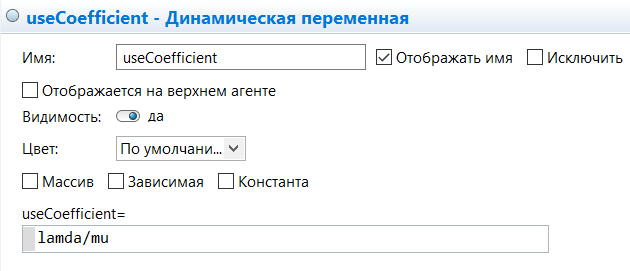 meanATMUsingTime – среднее время использования банкомата. Определяется путем обращения к функции mean() у данных гистограммы timeInSystemDistr  Чтобы отслеживать нагруженность банкомата, добавим столбиковую диаграмму со следующими свойствами: 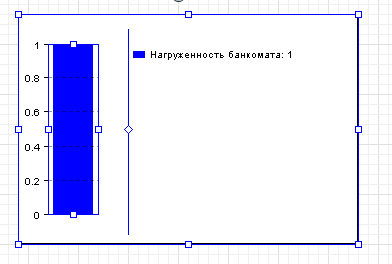 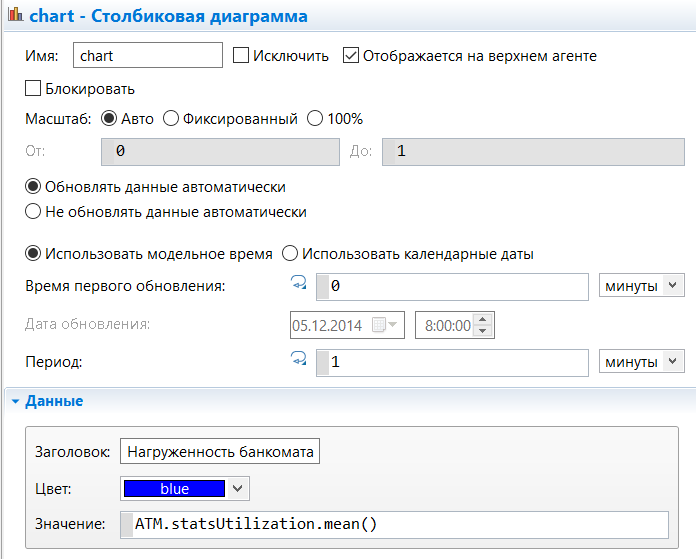 - отвечает за нагруженность банкоматаВся схема: 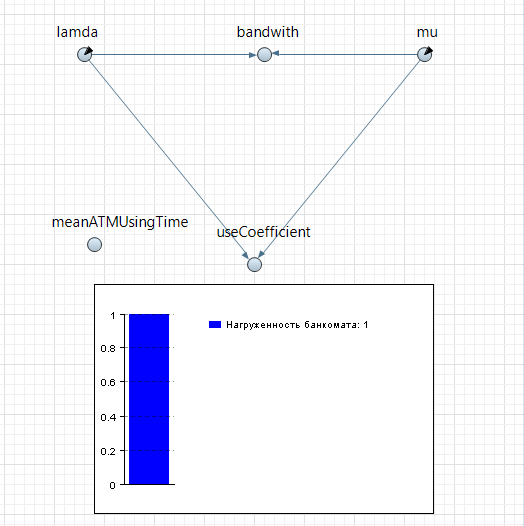 Чтобы интенсивность входного потока lamda и интенсивность обслуживания клиентов mu регулировать интерактивно, добавим ползунки lamdaParam и muParam. 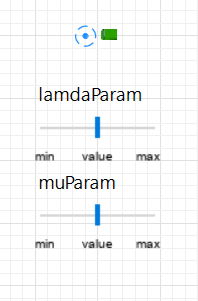 В свойствах lamdaParam пропишем следующее:  В свойствах muParam пропишем следующее:  Осталось добавить теоретический и практический коэффициенты использования, теоретическую и практическую абсолютную пропускную способности, теоретическую и практическую относительную способности. Для этого построим следующую схему: 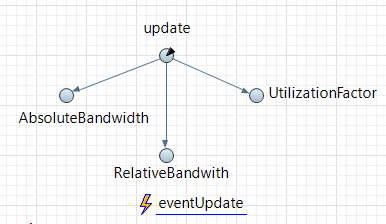 update – параметр, который связан с событием eventUpdate, обновляет нижеперечисленные параметры раз в минуту. AbsoluteBandwith – абсолютная пропускная способность. Значение задается с помощью выражения: sink.count() / (time() + update). Количество объектов в блоке sink, разделенное на время + параметр обновления. 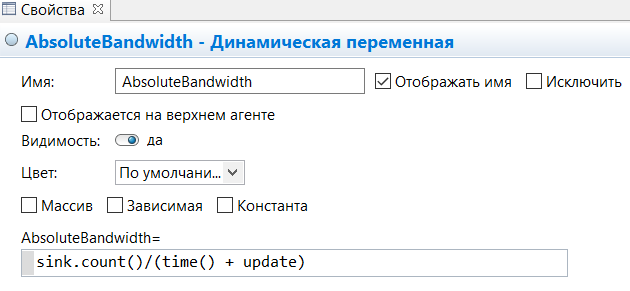 RelativeBandwith – относительная пропускная способность. Значение задается с помощью выражения: sink.count() / (source.countArrivals() + update) . Количество объектов в блоке sink, разделенное на количество прибывших агентов в блоке source + параметр обновления. 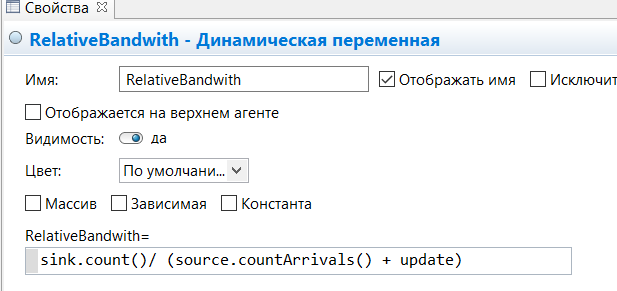 UtilizationFactor – фактор использования. Задается с помощью следующего выражения: source.countArrivals() / (sink.count() + update) . Количество прибывших агентов в блоке source, разделенное на количество агентов в блоке sink + параметр обновления. 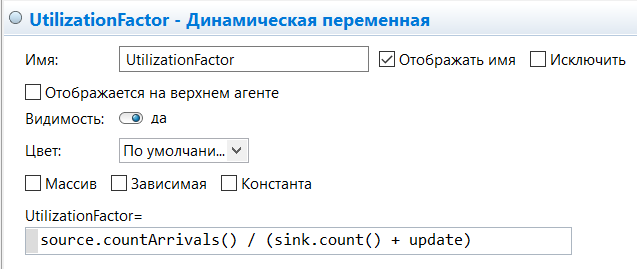 eventUpdate – событие, обновляет параметр update. 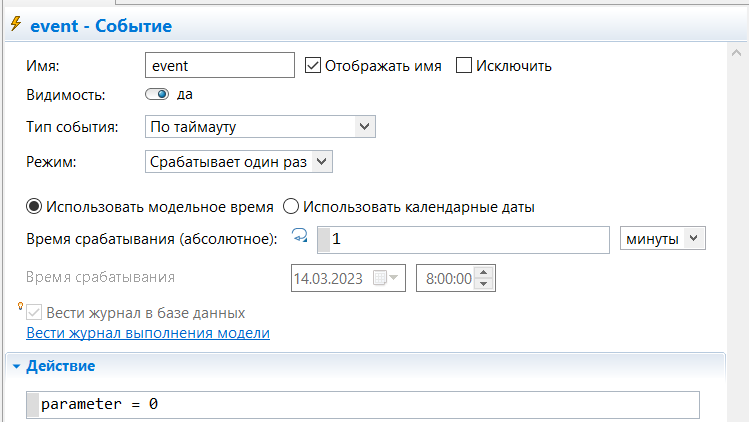 Добавим график, который измеряет теоретический и практический коэффициенты использования: 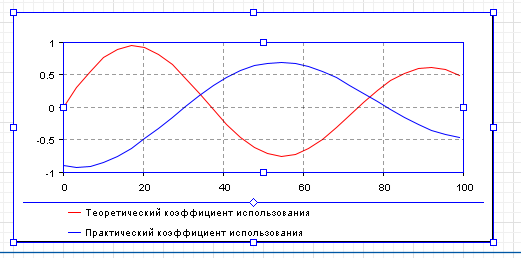 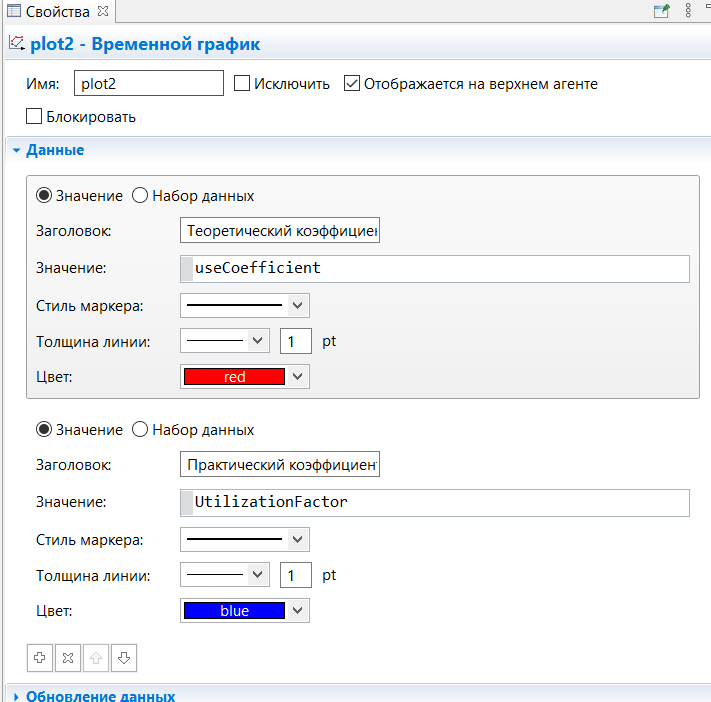 Добавим график, который измеряет теоретическую и практическую абсолютную способности:  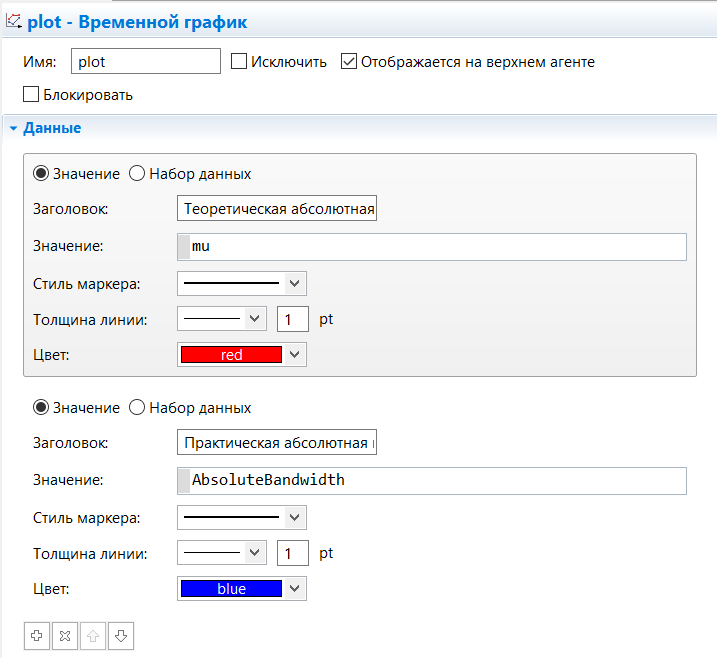 Добавим график, который измеряет теоретическую и практическую относительную способности: 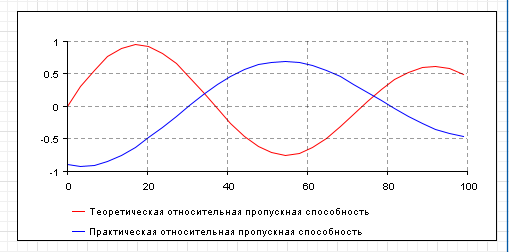  Общая схема: |
