Лабораторная работа №3. Отчет по лабораторной работе 3 "Определение ускорения свободного падения при помощи универсального маятника"
 Скачать 79.74 Kb. Скачать 79.74 Kb.
|
|
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ГОРНЫЙ ИНСТИТУТ (ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ) ОТЧЕТ По лабораторной работе №3 “Определение ускорения свободного падения при помощи универсального маятника” Выполнил: студент группы РГГ13 Шатохин А.С. Проверил: Ломакина Е.С. Санкт-Петербург 2013 Цель работы: определить ускорение свободного падения с помощью универсального маятника. Краткое теоретическое содержание: Наиболее точные измерения ускорения свободного падения выполняются с помощью косвенных методов. Многие из них основаны на использовании формул для периода колебаний математического и физического маятников. Математическим маятником называется материальная точка, подвешенная на невесомой, нерастяжимой нити и совершающая колебание в вертикальной плоскости под действием силы тяжести. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити. Период колебаний математического маятника 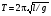 , (1) , (1)где l - длина маятника; [l]=м, g - ускорение свободного падения. [g]=м/  Ускорение g можно вычислить, измерив Т и l. Погрешность определения g в этом случае связана с тем, что реальный маятник, используемый в лабораторных условиях, может только с некоторым приближением рассматриваться как математический (чем больше l, тем точнее измерения). Физическим маятником называется абсолютно твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр тяжести. Период колебаний физического маятника 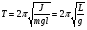 , (2) , (2)где J - момент инерции маятника относительно оси качаний (точки подвеса); m - его масса; [m]=кг, l- расстояние от центра тяжести до оси качаний.[l]=м. Величину L = J/(ml) называют приведенной длиной физического маятника. Она равна длине такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Зная T, m, lиJ можно по формуле (2) найти ускорение свободного падения g. Массу маятника и период его колебаний можно измерить с очень высокой точностью, но точно измерить момент инерции не удается. Указанного недостатка лишен метод оборотного маятника, который позволяет исключить момент инерции из расчетной формулы для g. Метод оборотного маятника основан на том, что во всяком физическом маятнике можно найти такие две точки, что при последовательном подвешивании маятника за одну или другую, период колебаний его остается одним и тем же. Расстояние между этими точками представляет собой приведенную длину данного маятника. 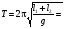 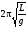 , где L- приведенная длина оборотного маятника , где L- приведенная длина оборотного маятникаРасчетные формулы: 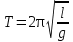 – период колебаний математического маятника, l – длина математического маятника [l]=1 м, g – ускорение свободного падения [g]= 9.8 м/ – период колебаний математического маятника, l – длина математического маятника [l]=1 м, g – ускорение свободного падения [g]= 9.8 м/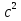 , [T]= 1 c. , [T]= 1 c.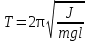 =2 =2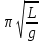 – период колебаний физического маятника , где J – момент инерции маятника относительно оси качаний [J]=1кг* – период колебаний физического маятника , где J – момент инерции маятника относительно оси качаний [J]=1кг*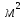 ,m-его масса [m]=1кг, l – расстояние от центра тяжести до оси качаний. ,m-его масса [m]=1кг, l – расстояние от центра тяжести до оси качаний.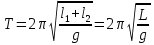 g=4 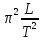 – измерение ускорения свободного падения с помощью оборотного маятника. – измерение ускорения свободного падения с помощью оборотного маятника.L=  – приведенная длина физ. маятника, которая равна длине такого математического маятника, период колебаний которого совпадает с периодом данного физ. маятника. – приведенная длина физ. маятника, которая равна длине такого математического маятника, период колебаний которого совпадает с периодом данного физ. маятника.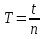 – где t-время колебаний маятника [t]=c, n-количество колебаний за время t. – где t-время колебаний маятника [t]=c, n-количество колебаний за время t.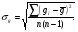 - средняя квадратичная ошибка для g измеренного при помощи математического маятника, где - средняя квадратичная ошибка для g измеренного при помощи математического маятника, где 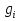 -результат одного вычисления, -результат одного вычисления, 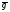 - средний результат, м/ - средний результат, м/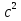 . .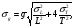 - средняя квадратичная ошибка для g измеренного при помощи оборотного маятника, где L – приведенная длина оборотного маятника [L]=м, - средняя квадратичная ошибка для g измеренного при помощи оборотного маятника, где L – приведенная длина оборотного маятника [L]=м, 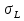 – погрешность измерения длины, оцениваемая по цене деления измерительной линейки. – погрешность измерения длины, оцениваемая по цене деления измерительной линейки.Схема установки: 10 11 2 1 8 3 4 5 7 9 6 С1 С2 1 – основание. 2 - математический маятник. 3 - винт. 4 - верхний кронштейн. 5 – винт. 6 - два диска. 7 – колонка. 8 - оборотный маятник. 9 - нижний кронштейн. 10 - фотоэлектрический датчик. 11 - универсальный электронный секундомер. Таблица: Расчеты для математического маятника:
Пример расчетов для опыта №1: 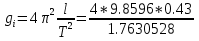 =9.6188339 м/ =9.6188339 м/ Расчет средней квадратичной ошибки для g: 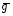 =9,6960514 м/ =9,6960514 м/ 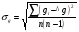 = =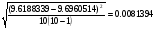 g=(9.6960514 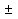 0.0081394)м 0.0081394)м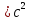 Расчеты для оборотного маятника:
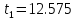 c c 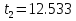 c c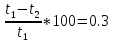  на 0,3% на 0,3% 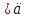 L=0.38 м L=0.38 мПример расчетов для опыта №1: 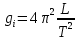 =4*9.8596* =4*9.8596* 9.5485935 м/ 9.5485935 м/ Расчет квадратичной ошибки для g: 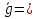 9.4774633 9.4774633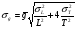 = = g=(9.4774633 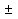 0.026)м/ 0.026)м/ Вывод: В данной лабораторной работе экспериментальным путем было определено ускорение свободного падения при помощи математического и физического маятников. Полученные результаты имеют небольшую погрешность относительно истинного значения, что позволяет говорить о точности расчётной формулы и о незначительных погрешностях при измерениях и вычислениях. |

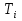 ,c
,c