Лабораторная работа N3. Отчет по лабораторной работе 3 Вынужденные колебания в rlc контуре
 Скачать 100.71 Kb. Скачать 100.71 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ КУРГАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра БИАС Электродинамика Отчет по лабораторной работе №3 «Вынужденные колебания в RLC-контуре»Выполнил: студент группы Т-3190 Черепанов И. А. Дата: 19.11.2012 Проверил: Москвин В. В. Курган, 2012 ЦЕЛЬ РАБОТЫ Знакомство с компьютерным моделированием процессов в колебательном RLC-контуре. Экспериментальное подтверждение закономерностей при вынужденных колебаниях в RLC-контуре. КРАТКАЯ ТЕОРИЯ Рассмотрим процессы, происходящие в контуре, содержащем конденсатор, катушку индуктивности, резистор и источник с переменной ЭДС, включенные последовательно и образующие замкнутую электрическую цепь. Если ЭДС источника меняется по гармоническому закону, то в контуре наблюдаются вынужденные гармонические колебания. При этом ток в контуре также будет переменным, подчиняющимся закону Ома в комплексной форме. КОМПЛЕКСНЫЙ ТОК и КОМПЛЕКСНОЕ НАПРЯЖЕНИЕ 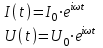 Здесь 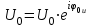 - комплексная амплитуда напряжения; - комплексная амплитуда напряжения; 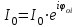 - комплексная амплитуда тока. - комплексная амплитуда тока.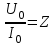 (импеданс). (импеданс). Импеданс – это отношение комплексной амплитуды напряжения на данном элементе, к комплексной амплитуде тока через данный элемент. Модуль импеданса называется ПОЛНЫМ ЭЛЕКТРИЧЕСКИМ СОПРОТИВЛЕНИЕМ цепи. 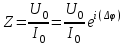 ; ; 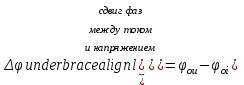 а) Резистор: 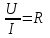 ; ; 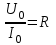 ; фазы напряжения и тока одинаковые. ; фазы напряжения и тока одинаковые. Импеданс равен R: ZR ≡ XR = R. б) Катушка индуктивности: Действует закон электромагнитной индукции (самоиндукции): 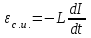 . . Использовав его и закон Ома для комплексных величин, получим: 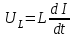 ; ; 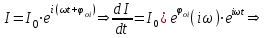 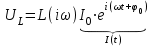 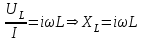  - импеданс катушки индуктивности. - импеданс катушки индуктивности.Напряжение на катушке опережает по фазе ток через нее на /2. в) Конденсатор: 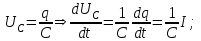 или или 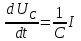 . .Пусть 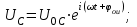 тогда тогда 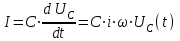 . . Найдем отношение 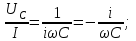 отсюда отсюда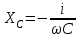 - комплексное сопротивление (импеданс) конденсатора. - комплексное сопротивление (импеданс) конденсатора.Напряжение на конденсаторе отстает по фазе от тока через него на /2. Модуль комплексного сопротивления (катушки или конденсатора) называется РЕАКТИВНЫМ СОПРОТИВЛЕНИЕМ (индуктивным или емкостным). Все элементы в контуре соединены последовательно, поэтому для нахождения импеданса контура надо просуммировать импедансы всех элементов: 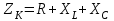 . После подстановки можем получить модуль импеданса т.е. полное сопротивление контура: . После подстановки можем получить модуль импеданса т.е. полное сопротивление контура: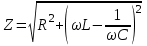 . .РЕЗОНАНСОМ для тока называется явление резкого увеличения амплитуды колебаний тока при приближении частоты ЭДС к некоторому значению, называемому резонансной частотой РЕЗ. Не трудно видеть, что максимум амплитуды тока будет тогда, когда минимально полное сопротивление контура, или ZРЕЗ = R и 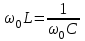 , отсюда , отсюда 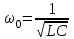 , что соответствует частоте свободных колебаний в контуре. , что соответствует частоте свободных колебаний в контуре.Максимум напряжения на конденсаторе соответствует резонансу для напряжения, который наблюдается при несколько меньшей частоте ЭДС: 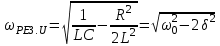 . . = 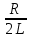 - коэффициент затухания для данного контура. - коэффициент затухания для данного контура.Амплитуда резонансного напряжения на конденсаторе U0C пропорциональна амплитуде ЭДС и добротности контура Q: U0C = Q0. При не слишком большом затухании в контуре добротность определяется соотношением: 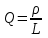 , где = , где = 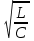 - называется характеристическим сопротивлением контура. Чем больше добротность, тем «острее» резонанс. - называется характеристическим сопротивлением контура. Чем больше добротность, тем «острее» резонанс.РЕЗОНАНСНОЙ КРИВОЙ называется зависимость амплитуды напряжения на конденсаторе от частоты ЭДС. МЕТОДИКА и ПОРЯДОК ИЗМЕРЕНИЙ Внимательно рассмотрите рисунок для компьютерной модели. 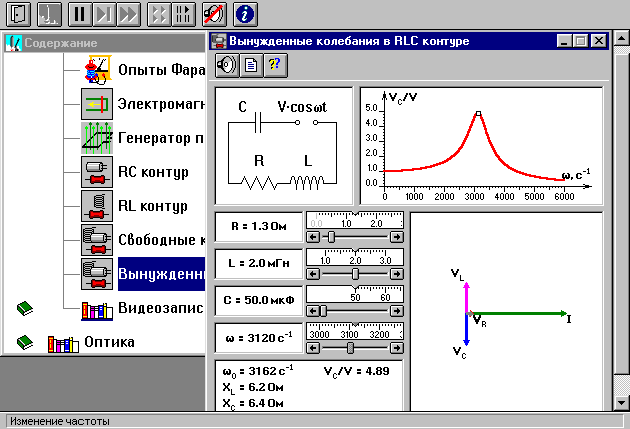 Перерисуйте необходимое в конспект, используя обозначения, принятые в нашей теоретической части (0 вместо V , U0C вместо VC , U0L вместо VL и U0R вместо VR). ИЗМЕРЕНИЯ: Изменяйте величину емкости конденсатора и наблюдайте изменение резонансной кривой. Зацепив мышью, перемещайте движки регуляторов R – сопротивления резистора, L – индуктивности катушки, и зафиксируйте значения, указанные в табл. 2 для вашей бригады. Установите указанное в табл.1 значение емкости конденсатора. Изменяя величину частоты ЭДС, следите за перемещением отметки на резонансной кривой и числовым значением добротности (U0C/0). Добейтесь максимального значения добротности и соответствующие значения частоты источника ЭДС и собственной частоты контура занесите в табл.1. Повторите измерения для других значений емкости конденсатора из табл.1. Повторите измерения для двух других значений индуктивности катушки, выбирая их из табл.2. Полученные результаты запишите в табл.3 и 4. ТАБЛИЦА 1. Значения характеристик.
ТАБЛИЦА 2. результаты измерений L =1,6 мГн.
L =1,3мГн.
L =3 мГн.
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА Постройте на одном листе графики зависимости резонансной частоты от корня из обратной емкости при трех значениях индуктивности. 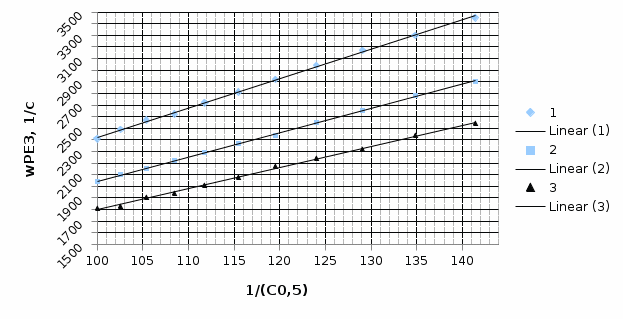 Котангенс угла наклона для каждой прямой: ctg() = 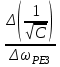 AЭКСП. AЭКСП.AЭКСП 1= 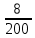 =4 =4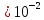 AЭКСП 2= AЭКСП 2= 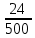 =4,8 =4,8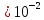 AЭКСП 3= AЭКСП 3= 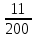 =5,5 =5,5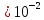 Теоретическое значение константы АТЕОР для каждой прямой: АТЕОР = 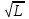 . .АТЕОР1= 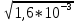 =4 =4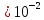 АТЕОР2= 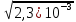 =4,8 =4,8 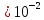 АТЕОР3= 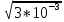 =5,48 =5,48 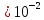 Таблица результатов измерений:
Вывод. В ходе выполнения данной лабораторной работы мы ознакомились с компьютерной моделью процесса вынужденных колебаний в RLC-контуре, произвели экспериментальное исследование закономерностей вынужденных колебаний, зависимости резонансной частоты от корня из обратной емкости при трех значениях индуктивности. Из графика видно, что: при увеличении индуктивности катушки, график резонансной частоты располагается выше; зависимости резонансной частоты от корня из обратной ёмкости является линейной. По графикам зависимости резонансной частоты от корня из обратной ёмкости были получены экспериментальные значения константы AЭКСП для каждой прямой, достаточно близкие к теоретическим значениям для этих же прямых. Некоторое отличие экспериментального значения может быть обусловлено неточностью графического метода измерения. |