ппппп. Лаб.раб.5-30.. Явление самоиндукции
 Скачать 86 Kb.
|
|
Омский государственный технический университет Кафедра физики Отчёт по лабораторной работе № 5-30 ЯВЛЕНИЕ САМОИНДУКЦИИВыполнил(а): студент группы ____________________ ___________________________________ Проверил(а): ___________________________________ Дата: ______________ Лабораторная работа № 5-30 ЯВЛЕНИЕ САМОИНДУКЦИИЦель работы: изучить зависимость постоянной времени электрической цепи, состоящей из катушки индуктивности и резистора, от величины сопротивления резистора; определить величины индуктивности катушки и магнитной проницаемости сердечника катушки. Приборы и принадлежности: генератор прямоугольных импульсов ГН1, лабораторный стенд, электронный осциллограф «PicoScope 2203». Краткая теория Явление самоиндукции заключается в …………………………………………….. ……………………………………………………………………………………….…… ………………………………………………………………………………….………… Возникающая в контуре ЭДС самоиндукции рассчитывается по формуле: в которой буквой Ψ обозначается………………………………………………… при этом потокосцепление самоиндукции контура пропорционально………… ….……………………………………………………………………………………….. Коэффициент пропорциональности этих величин называется индуктивностью и обозначается буквой ……. Индуктивность зависит от ………………………………………………………….. ……………….…………………………………………………………………………… Например, индуктивность длинного соленоида (катушки) выражается формулой: При постоянной индуктивности ЭДС самоиндукции, возникающая в контуре, рассчитывается по формуле: Знак «минус» в этой формуле означает, что ЭДС самоиндукции …………….... …………………………………………………………………………………………… Таким образом, из-за самоиндукции сила тока в контуре, обладающем индуктивностью, не может измениться мгновенно. Рассмотрим электрическую цепь, состоящую из резистора с активным сопротивлением R, катушки с индуктивностью L и генератора прямоугольных импульсов ЭДС с амплитудой ε0 (рис.1). В 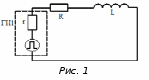 момент начала импульса ЭДС сила тока в цепи, а значит и напряжение на резисторе начинают нарастать постепенно (рис. 2) согласно формуле:В момент окончания импульса ЭДС сила тока в цепи и напряжение на резисторе начинают убывать постепенно (рис. 3) согласно формуле: 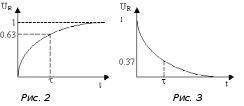 Величина  называется ……………………………………………………..Она равняется времени, за которое при нарастании тока величина напряжения на резисторе достигает значения U = 0,63 Umax (рис. 2), а при убывании тока напряжение на резисторе уменьшается до U = 0,37 Umax (рис. 3), то есть уменьшается в е раз. Поскольку реальные источники ЭДС и катушки индуктивности обладают суммарным собственным сопротивлением r, то постоянная времени: τ = L/(R+r) то есть 1/τ = R/L+r/L. Как видно из последнего выражения, зависимость 1/τ от R является линейной. Экспериментально найдя эту зависимость, можно определить индуктивность контура. Экспериментальная часть 1 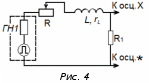 . Соберите электрическую схему согласно рис. 4.2. С помощью электронного осциллографа измерьте постоянную времени цепи τ, изменяя сопротивление реостата R от 100 до 500 Ом с шагом 100 Ом. Полученные результаты занесите в таблицу 1. Таблица 1
Обработка результатов измерений 1. Рассчитайте величины 1/τ для каждого значения R и занесите в таблицу 1. 2. Постройте график зависимости 1/τ = f(R) и убедитесь, что зависимость является линейной. 3. Рассчитайте величину индуктивности L по графику зависимости 1/τ = f(R), где L является величиной, обратной тангенсу угла наклона прямой  . 4. Определите магнитную проницаемость сердечника соленоида по формуле 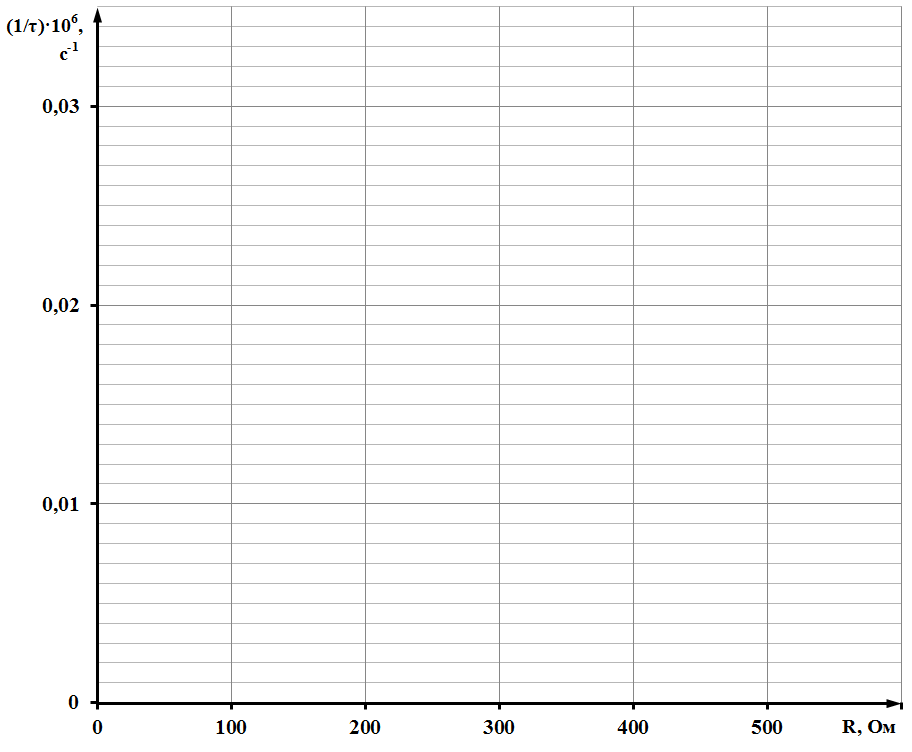 при заданных параметрах соленоида: S = 0.64 см2, l = 10 мм, N=30.  Выводы В данной лабораторной работе изучалось явление …………...…………………… С помощью генератора прямоугольных импульсов ЭДС создавали колебания тока в цепи, состоящей из ……………………………………………………………… ……………………………………………………………………………………...…….. Наблюдая осциллограммы зависимости напряжения на резисторе цепи от времени, убедились, что…………………………………………………………………… …………………………………………………………………………………………… С помощью электронного осциллографа измерили……………………………….. ……………………………………………………………………………………………. ……………………………………………………………………………………………. Рассчитали величины ……………………………………………..………...……….… и построили график зависимости………………………………………….………….. …………………………………………………………………………………………… Зависимость получилась ………………………., что ……………………….. теории. По наклону графика определили……………………………………………………… …………………………………………………………………………………………… Рассчитали ……………………………………………………………………………… …………………………………………………………………………………………… Полученное значение указывает на то, что сердечник соленоида выполнен из ……………………………………………………. материала |