Лаба 4. Отчет по лабораторной работе 4 проверка теоремы гюйгенса штейнера методом вращательных колебаний
 Скачать 61.79 Kb.
|
|
Федеральное государственное автономное образовательное учреждение высшего образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)» кафедра физики ОТЧЕТ по лабораторной работе № 4 «ПРОВЕРКА ТЕОРЕМЫ ГЮЙГЕНСА – ШТЕЙНЕРА МЕТОДОМ ВРАЩАТЕЛЬНЫХ КОЛЕБАНИЙ» Выполнил: Кононок Я.Ф. Группа № 2281 Преподаватель: Мыльников И.Л.
Цель работы. Определение момента инерции эталонного диска методом вращательных колебаний и экспериментальная проверка теоремы Гюйгенса-Штейнера  Приборы и принадлежности. Лабораторная установка (рис. 4.1) включает колебательную систему, вращающуюся в горизонтальной плоскости, которая состоит из закрепленного на вертикальной оси диска (шкива) 1, ремень 2 которого связан с упругими пружинами 3, зацепленными за штыри стойки. К шкиву жестко прикреплен металлический профиль 4 с рядом отверстий 5, в которых фиксируются грузы 6. Исследуемые закономерности Период колебаний T подвижной части колебательной системы, используемой в работе, связан с ее моментом инерции I. Выведем эту зависимость. В положении равновесия силы упругости пружин, а, следовательно, и силы натяжения нити с разных сторон диска (шкива) одинаковы. Обозначим эти силы F0. Для выведения шкива из положения равновесия повернем его на угол . По закону Гука силы упругости изменятся на kd/2, здесь k – коэффициент жесткости системы последовательно соединенных пружин d – диаметр шкива. Тогда натяжение одной пружины увеличится, а другой уменьшится на kd/2, и на шкив будет действовать возвращающий момент сил: М= 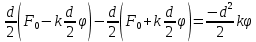 (1)Подставляя (1) в основное уравнение динамики вращательного движения M=Iε (2) и учитывая, что  , получаем дифференциальное уравнение для :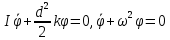 которое имеет вид дифференциального уравнения гармонического осциллятора. Из теории дифференциальных уравнений известно, что его решение имеет вид: 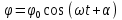 Здесь 0 и – константы, определяемые начальными условиями, а  (3) – собственная частота колебаний рассматриваемого маятника. Если обозначить I0, ω0, T0 соответственно момент инерции, частоту и период системы, в которой грузы 6 (рис. 4.1) помещены на металлическом профиле 4 в центр шкива 1, то согласно формуле (3):  (4)Если грузы переместить симметрично относительно оси вращения системы вдоль металлического профиля на шкиве в положения (1-1), (2-2) и т.д., то момент инерции I , частота и период T колебательной системы изменятся, и ее момент инерции станет равным: 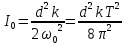 (5)Из (4), (5) видно, что отношение моментов инерции равно: 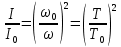 (6)Если радиус цилиндров R , а их масса m, то при установке цилиндров на расстоянии r от оси вращения колебательной системы ее момент инерции равен 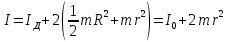 (7)где Iд момент инерции диска 1 с металлическим профилем 4, 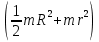 – момент инерции одного цилиндра, рассчитанный согласно теореме Гюйгенса-Штейнера, 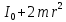 – постоянная часть момента инерции колебательной системы. С учетом формул (6), (7) выражение для I0 имеет вид: (8)Формула (8) получена при использовании теоремы Гюйгенса-Штейнера, а значит, хотя и косвенным образом, может быть использована для проверки правильности этой теоремы. Для этого достаточно убедиться, что значения моментов инерции I0 , определенные при разных положениях цилиндров относительно оси вращения колебательной системы примерно одинаковы. Если момент инерции I0 определен, то из формулы (4) можно найти жесткость колебательной системы в данном эксперименте:  (9)
Вопросы Какой физический смысл момента инерции? Как определить момент инерции точечной массы, сплошного тела и составного тела? Момент инерции - величина, характеризующая распределения масс в теле и являющаяся наряду с массой мерой инертности тела при вращательном движении. Момент инерции является мерой инертности тела при вращении. Моментом инерции материальной точки называют произведение массы точки на квадрат расстояния до оси вращения. J=miri2 Чтобы найти момент инерции тела, надо просуммировать момент инерции всех материальных точек, составляющих данное тело. J=ʃr2dm Момент инерции составного тела равен сумме моментов инерции составных частей. J=∑Ji | |||||||||||||||||||||||||||||||||||||||||||||||||||||