резонанс в электрической цепи. Отчет по лабораторной работе 5 Резонанс Выполнил студент группы 0401 Гробов Валерий Павлович
 Скачать 1.72 Mb. Скачать 1.72 Mb.
|
|
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Отчет по лабораторной работе № 5 Резонанс Выполнил студент группы 0401 Гробов Валерий Павлович Проверил преподаватель Обходский Артём ВикторовичТомск-2021 Цель работы: приобрести и закрепить теоретические знания и практические навыки исследования явления резонанса в линейных электрических цепях Основные задачи: Научиться экспериментально выявлять резонансный режим работы цепи с помощью измерительных приборов. Проводить теоретические расчеты резонансной частоты. Анализировать и аргументировано объяснять результаты экспериментальных и теоретических расчетов Приобрести навыки получения, анализа и аргументированного объяснения характера экспериментальных зависимостей характеристик колебательного контура от рабочей частоты источника ЭДС при резонансе токов и напряжений Приобрести навыки исследования и аргументированного обоснования характера зависимости напряжения на реактивном элементе от добротности контура Ход работы Исследование резонанса токов Собрана схема для исследования резонанса токов,   а) б) 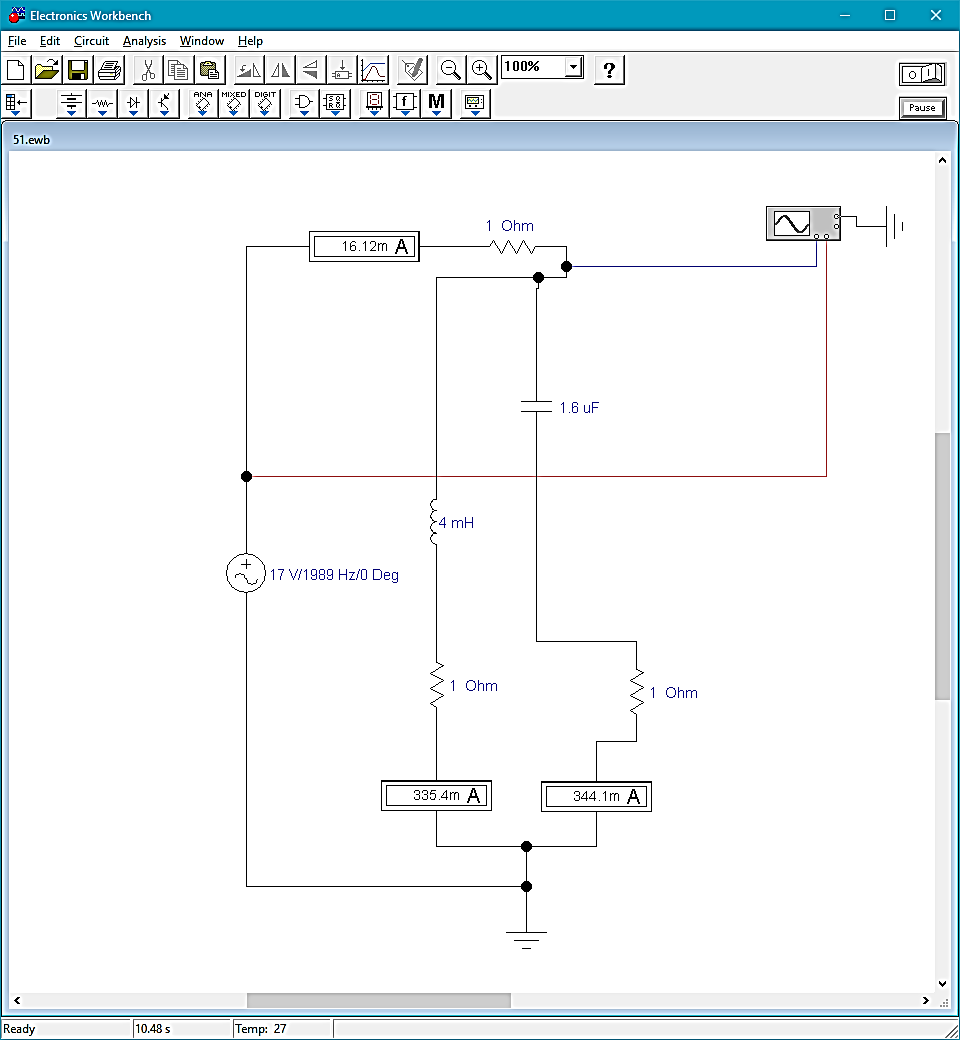 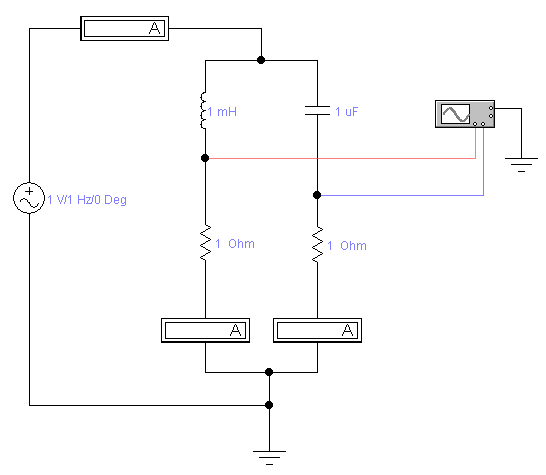 Рис 1. схема для исследования резонанса токов Установлены значения емкости конденсатора, индуктивности катушки и ЭДС источника в соответствии с полученным вариантом (см. табл. 1), а сопротивления резисторов – 1 Ом, чтобы мгновенное значение напряжения на резисторах будет численно равно мгновенному значению тока в ветвях. Табл.1
Рассчитана резонансная частота полученного контура. Условие наступления режима резонанса токов в схеме: 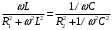 Когда 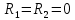 , частота , частота 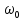 , при которой возникает резонанс токов (резонансная частота без потерь), принимает значение: , при которой возникает резонанс токов (резонансная частота без потерь), принимает значение: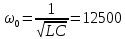 Рабочая частота источника ЭДС: 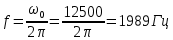 Установлена рабочая частота источника ЭДС равной резонансной частоте контура. Факт возникновения резонансного режима установлен по показаниям амперметров и осциллографа. Показания амперметра в неразветвленной части цепи: 16,13 мА Показания амперметра в разветвленной части цепи: 335,7 мА, 344,4 мА осциллограммы сигналов: 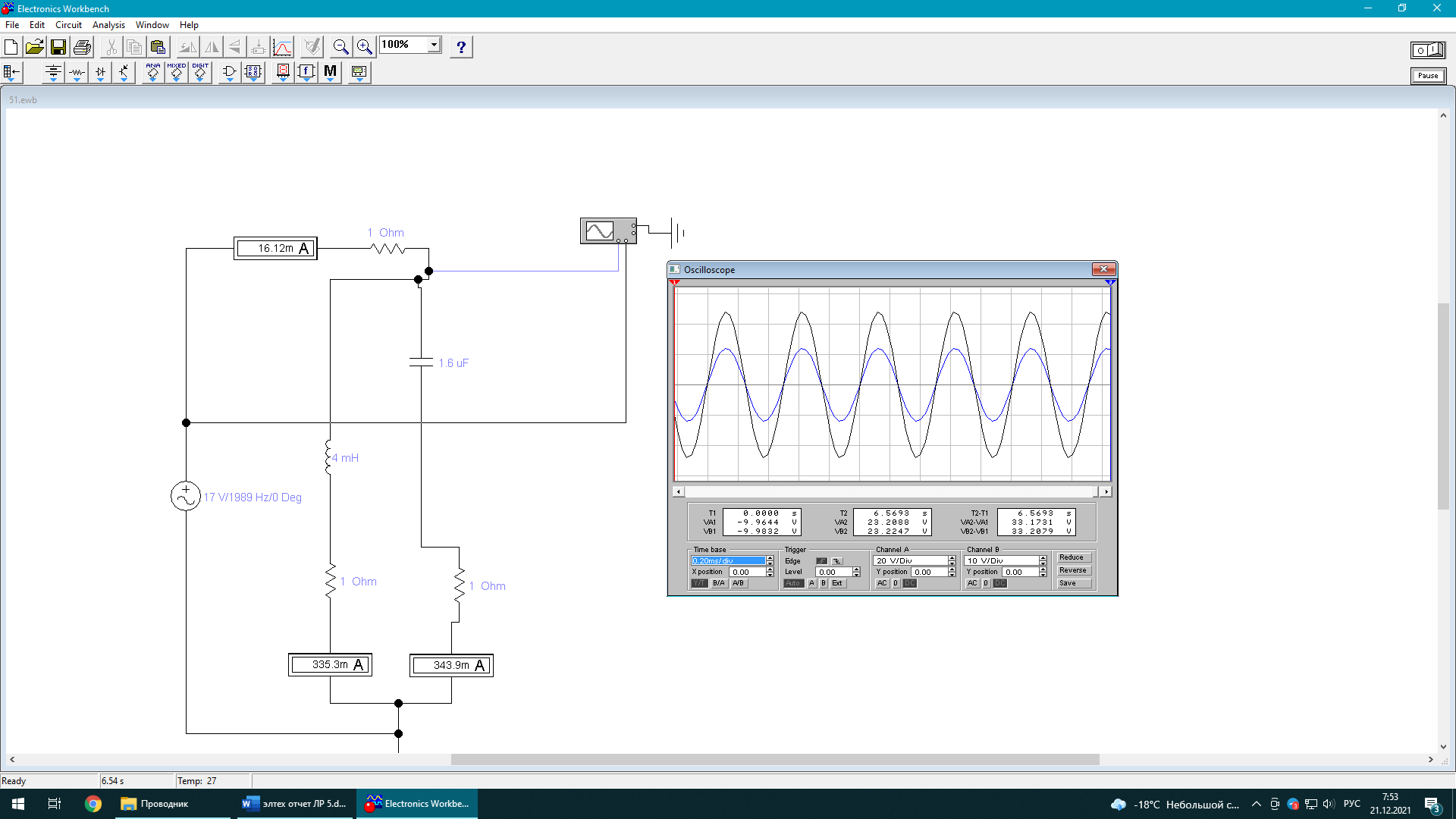 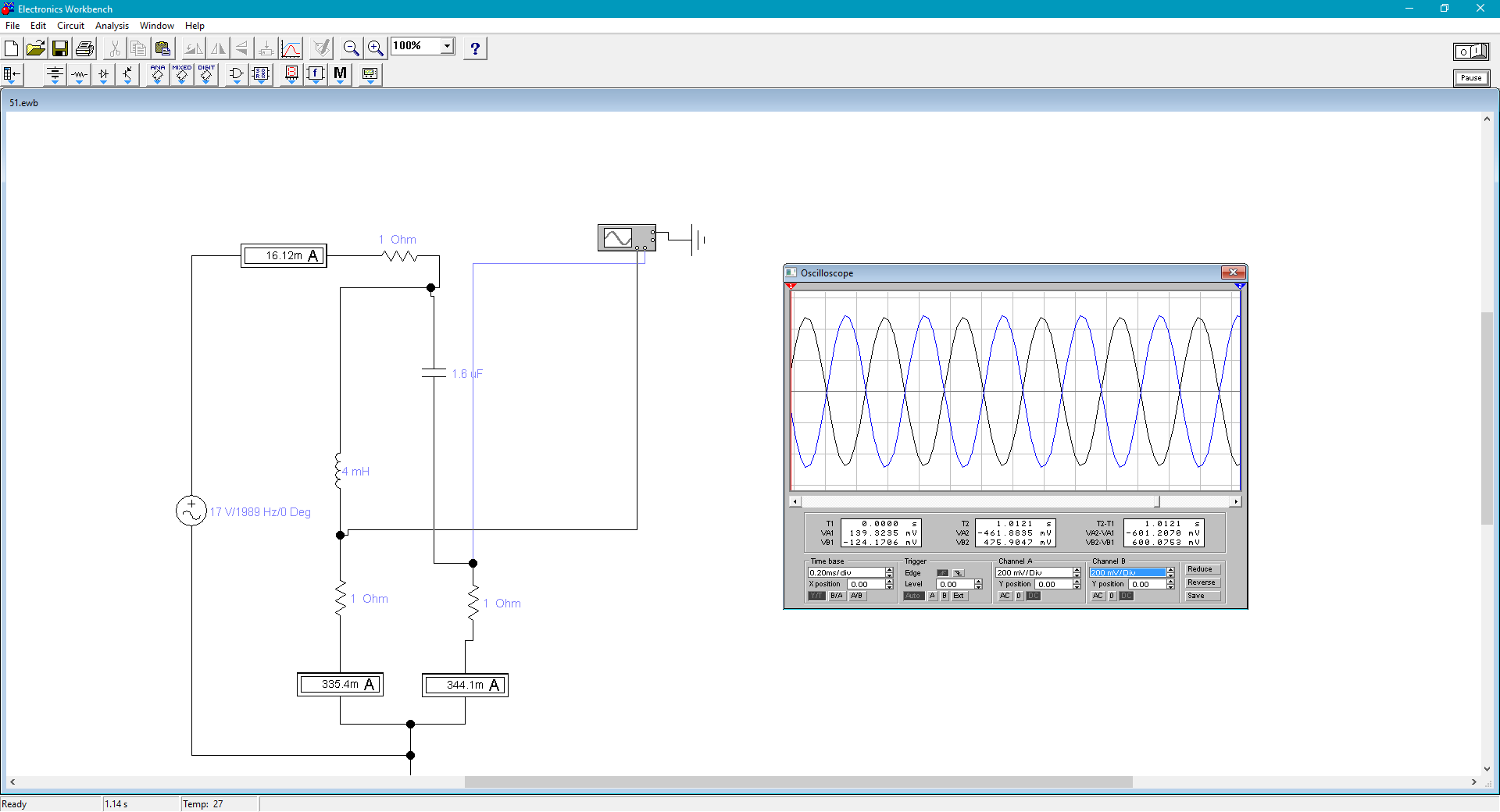   Рис. 2 «Осциллограмма сигналов на входе» Рис 3 рис.3 «Осциллограмма сигналов в разветвленной части цепи» Объяснение полученного результата. Рис.2: при установлении резонансной частоты, выполнились условия наступления резонанса тока. По закону Ома, при выполнении условия резонанса, полное сопротивление контура приняло минимальное значение, а ток в ветвях C и L максимальное. Рис.3: ток на индуктивном элементе не совпадает по фазе с током емкостного элемента на π рад. Это можно объяснить тем, что напряжение на индуктивном элементе опережает ток по фазе на 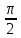 , напряжение на емкостном элементе отстает от тока по фазе на , напряжение на емкостном элементе отстает от тока по фазе на 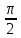 , и, складывая эти разности, можно получить разность фаз между напряжением на индуктивном и напряжением на ёмкостном элементах величиной равной π рад. , и, складывая эти разности, можно получить разность фаз между напряжением на индуктивном и напряжением на ёмкостном элементах величиной равной π рад.Изменяя значение рабочей частоты источника ЭДС от 0 до 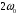 , где , где 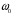 – резонансная частота контура с шагом – резонансная частота контура с шагом 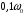 , построена зависимость сопротивления контура от рабочей частоты источника ЭДС. , построена зависимость сопротивления контура от рабочей частоты источника ЭДС.Сопротивление контура будет равно:  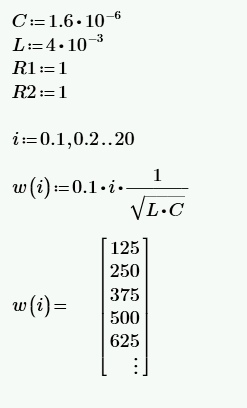 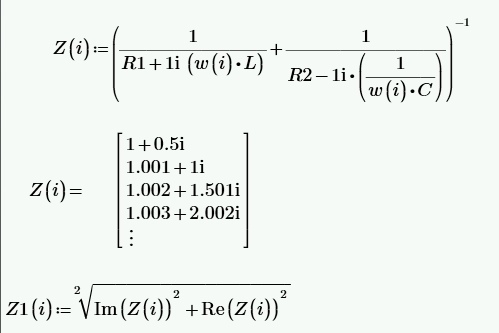 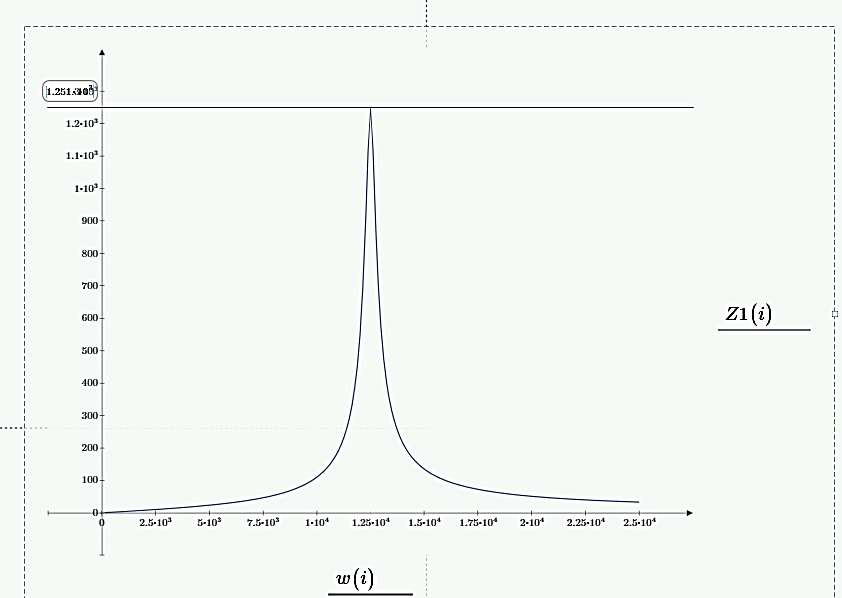 Рис.4 График зависимости сопротивления контура от рабочей частоты источника ЭДС. Согласно графику рис.4 при резонансной частоте полное сопротивление цепи приняло максимальное значение, потому что общий ток в неразветвленной части цепи оказался равным нулю, а токи в параллельных ветвях приняли максимальное значение, т.е. произошло явление резонанса тока. Введя контур в резонансный режим, разорвана ветвь, содержащая конденсатор: 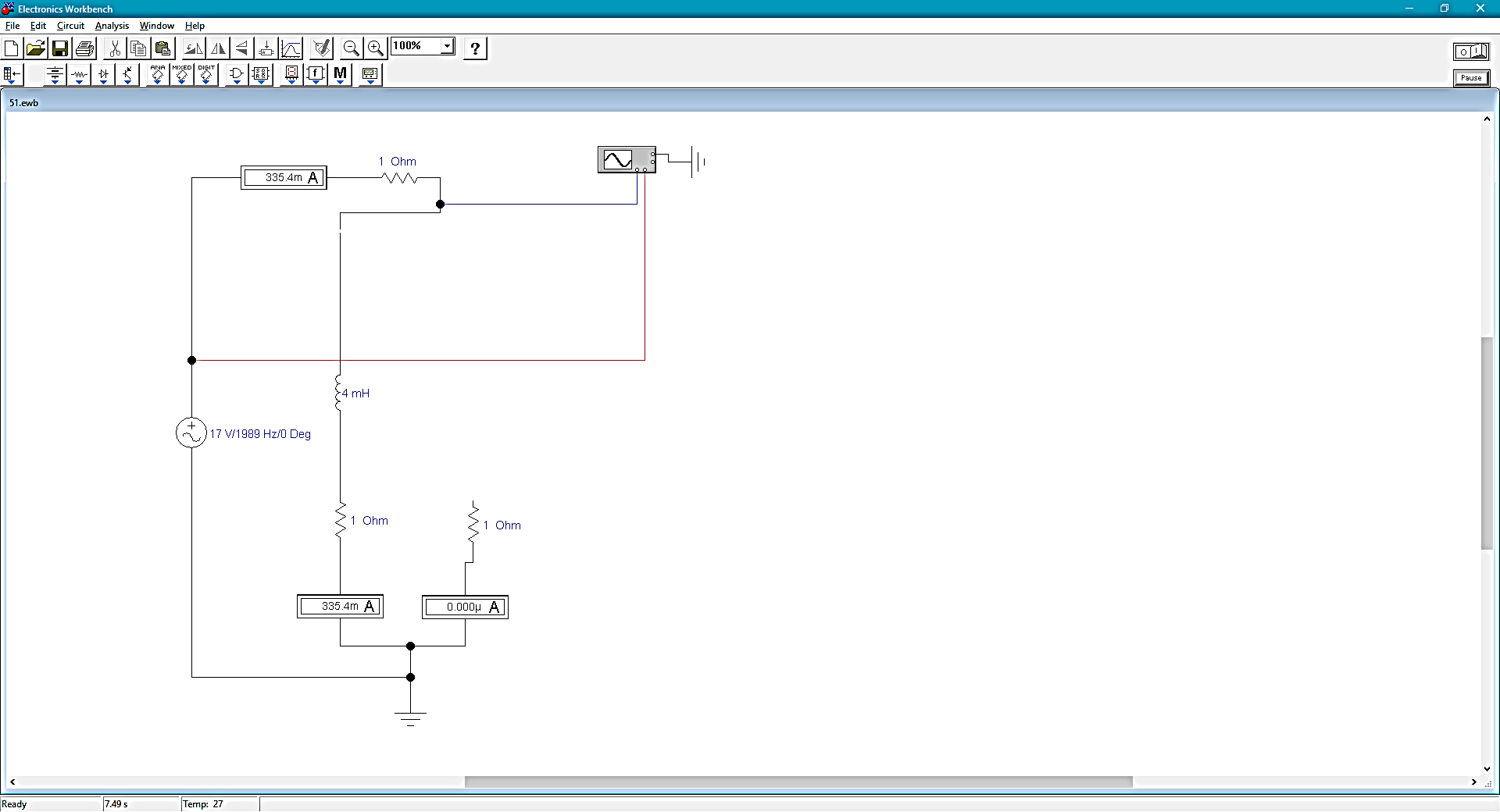 Рис. 4 цепь с разрывом ветви, содержащей конденсатор показания амперметра в неразветвленной части цепи 335,4 мА показания амперметра в разорванной ветви 335,4 мА Увеличение тока в подводящих проводах произошло из-за резкого падения сопротивления. Исследование резонанса напряжений Собрана схема для исследования резонанса напряжений,  а)  б) 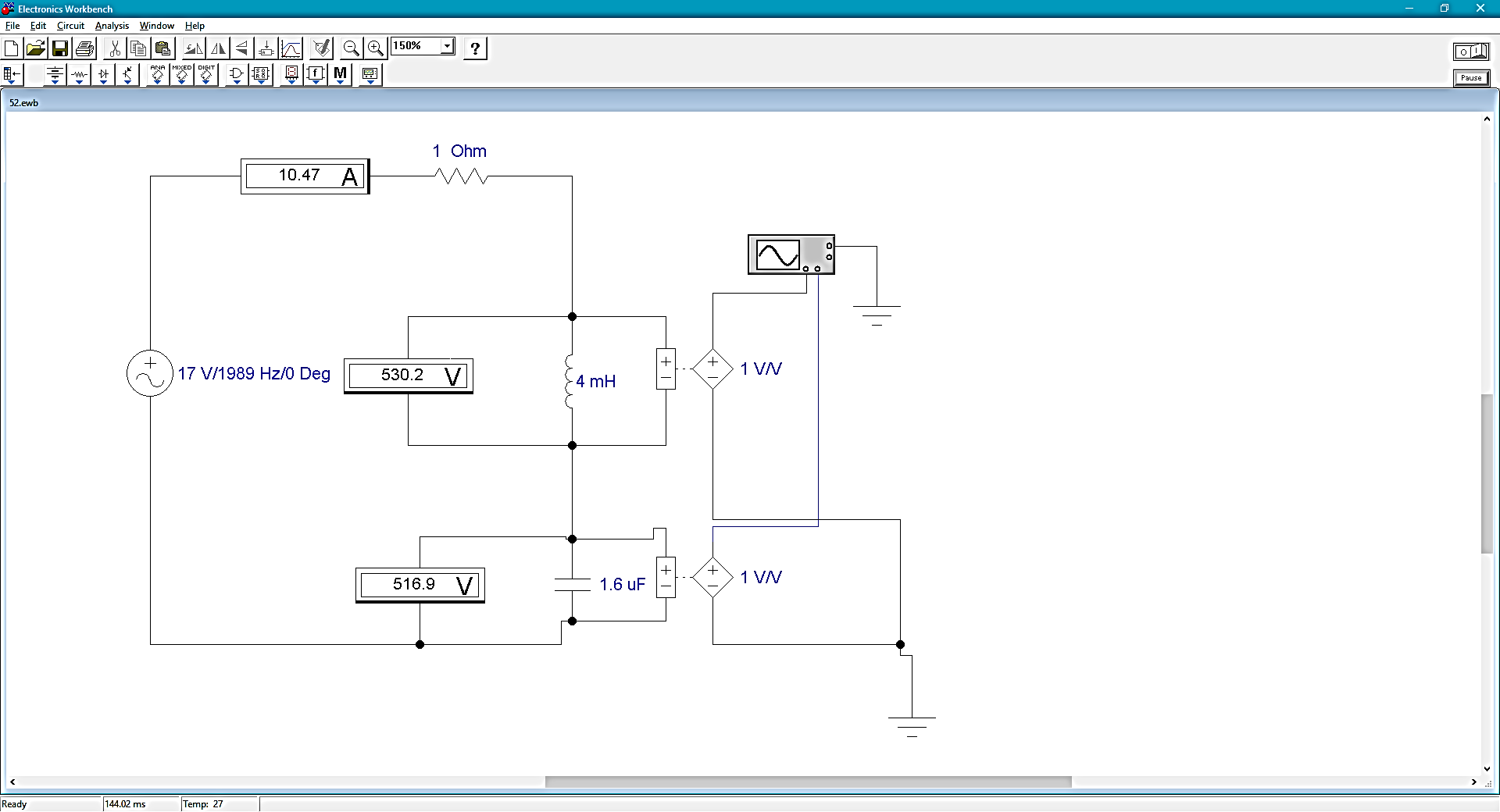 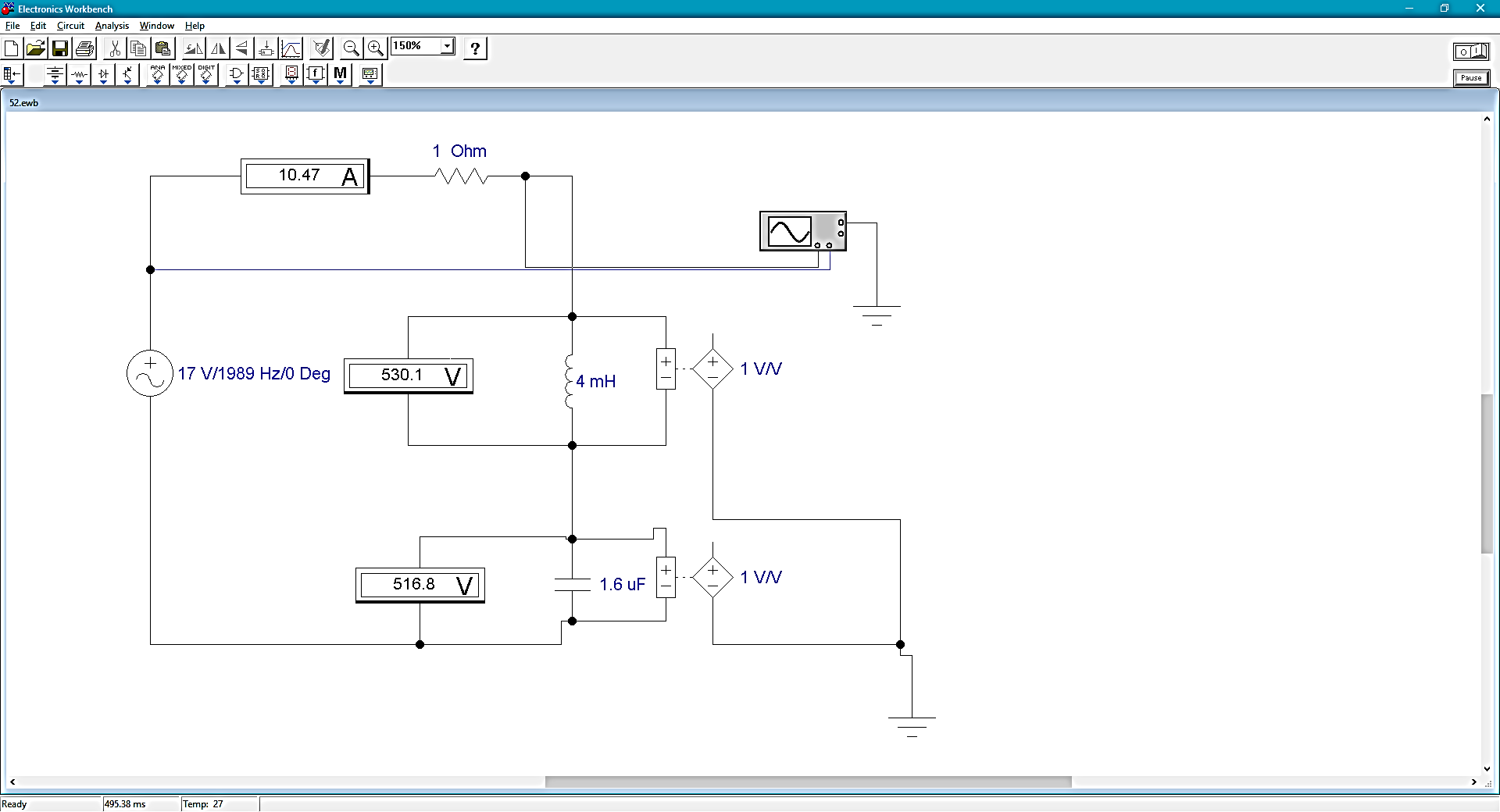 Рис.5 схема для исследования резонанса напряжений Установлены значения емкости конденсатора, индуктивности катушки и ЭДС источника в соответствии с полученным вариантом (см. табл. 1), а сопротивления резистора – 1 Ом. Источники напряжения, управляемые напряжением (ИНУН), введены в данную схему для обеспечения возможности измерений с помощью осциллографа. Коэффициент передачи ИНУН установлен равным 1 В/В. Следовательно мгновенное значение напряжения на выходе ИНУН будет численно равно мгновенному значению напряжений на конденсаторе и катушке. Рассчитаная резонансная частота полученного контура. 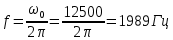 Установлена рабочая частота источника ЭДС равная резонансной частоте контура. Факт возникновения резонансного режима установлен по показаниям вольтметров, амперметра и осциллографа.   Рис.7 осциллограмма сигналов на входе (при подключении осциллографа б) Рис.6 осциллограмма сигналов индуктивного и ёмкостного элементов (при подключении осциллографа а) 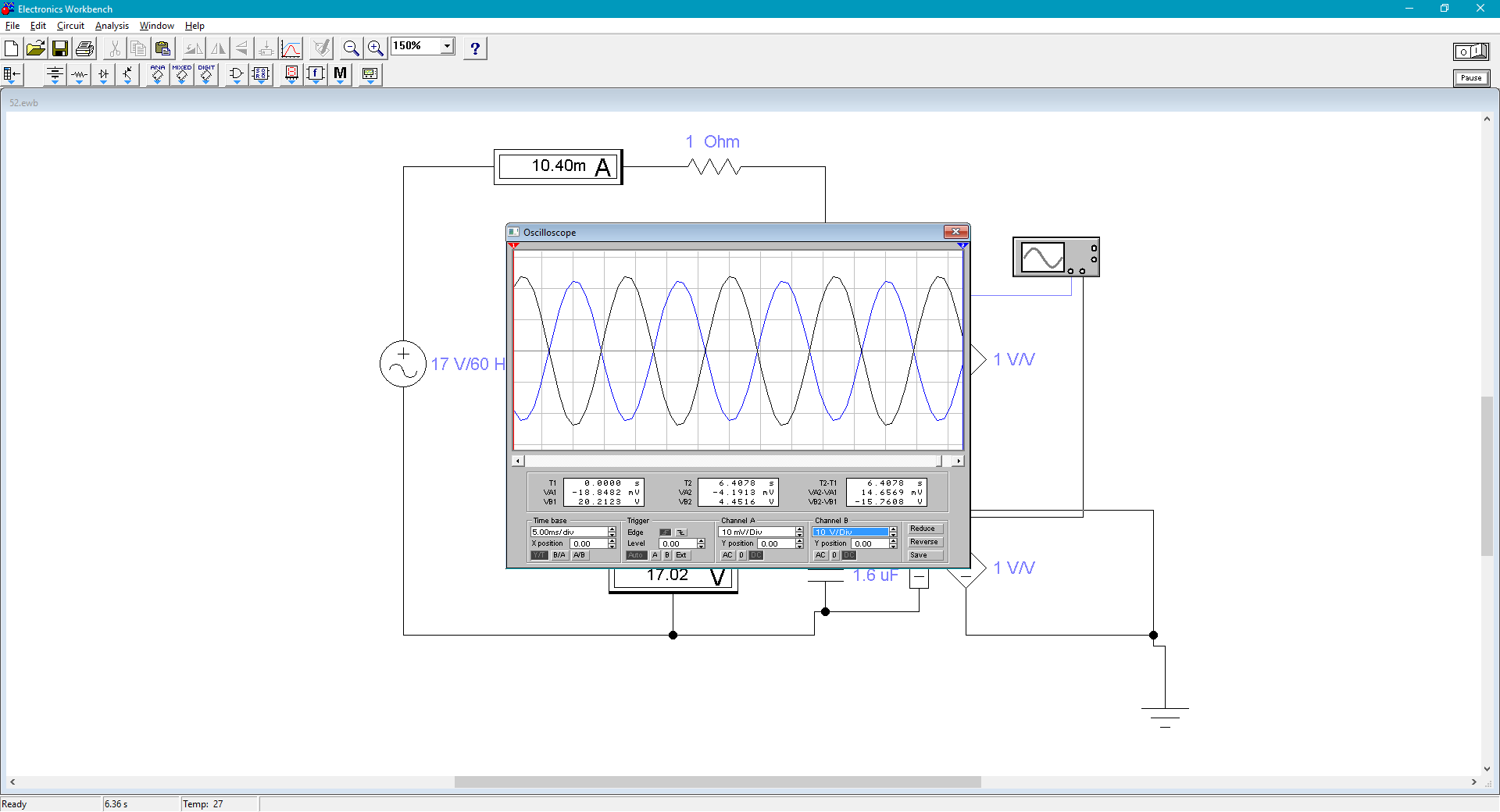 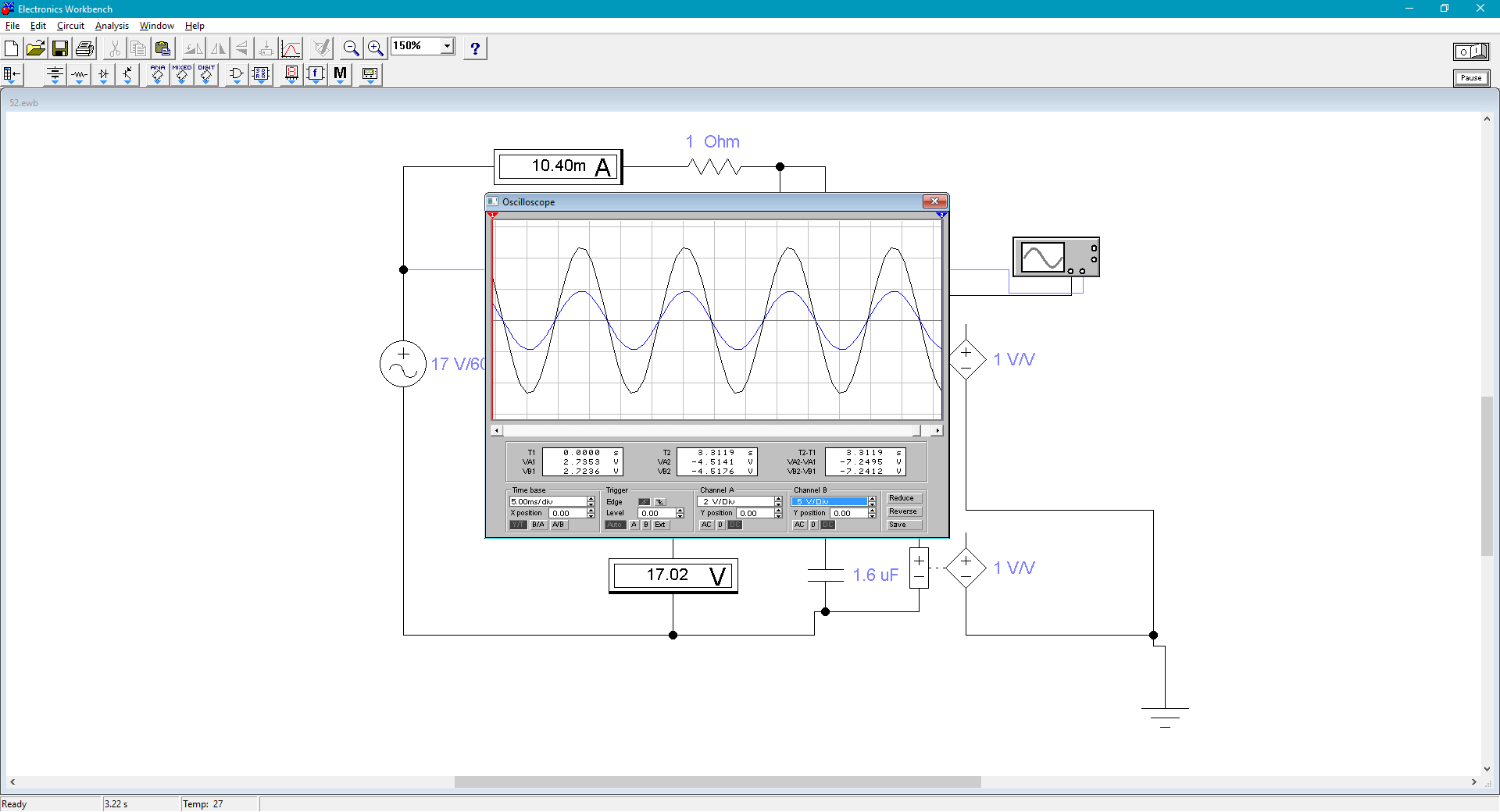 показания вольтметров и амперметра: V (L): 530,2 В V(C): 516,9 В A: 10,47 А По показаниям вольтметра и осциллографа, установлен факт возникновении резонанса напряжения, так как общее напряжение цепи совпадает по фазе с током (фазный резонанс), что можно наблюдать на Рис. 7. В то время как напряжения на ёмкостном и индуктивном элементах одинаковы по амплитуде и противоположны по фазе (рис. 6). По показаниям амперметра рассчитано сопротивление контура в резонансном режиме. Закон Ома в показательной форме: 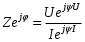 При резонансе, фаза тока совпадает с фазой напряжения, следовательно, сдвиг фазы равен φ=0. Тогда: 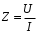 Согласно условию резонанса, в контуре будет только активное сопротивление, значит: 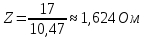 Напряжение на индуктивном элементе равно: 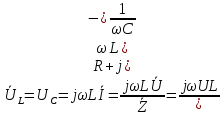 Изменяя значение рабочей частоты источника ЭДС от 0 до 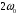 , где , где 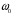 – резонансная частота контура с шагом – резонансная частота контура с шагом 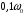 , построена зависимость напряжения на любом реактивном элементе от рабочей частоты источника ЭДС , построена зависимость напряжения на любом реактивном элементе от рабочей частоты источника ЭДС 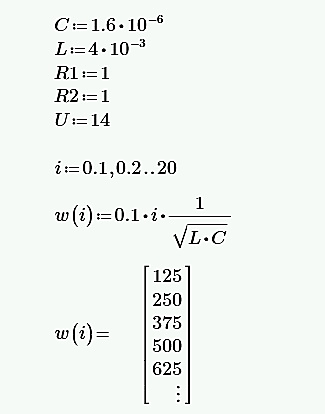 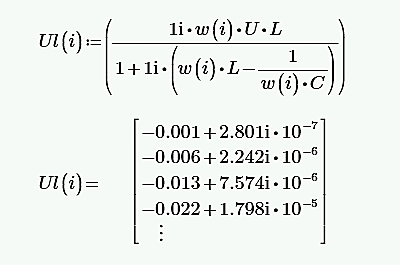 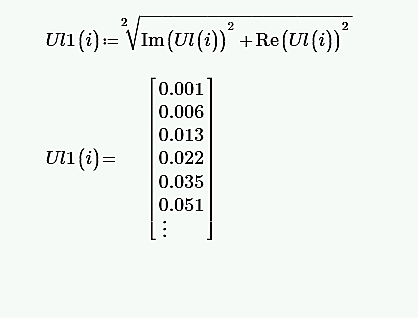 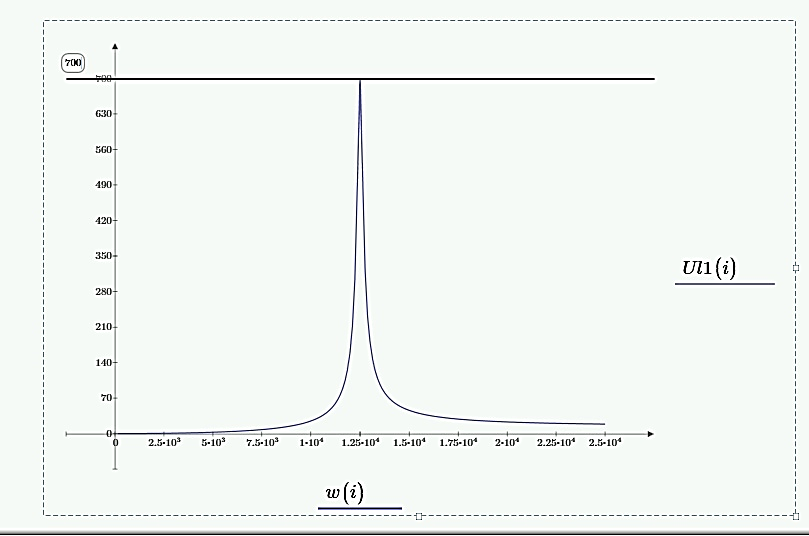 Рис.9 график зависимости напряжения контура от рабочей частоты источника ЭДС Объяснение полученной зависимости: В момент выполнения условия резонанса, полное сопротивление цепи становится минимальным, тогда ток при заданном ЭДС достигает наибольшего значения, следовательно, и напряжение на индуктивном и ёмкостном элементах принимает максимальное значение, что отражается соотношениями: 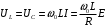 Проделан пункт 2.8 для 3-х различных значений добротности контура. Различные значения добротности получены изменением активного сопротивления контура. Формула для расчета добротности: 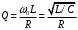  Таблица 2 «Значения различной добротности»
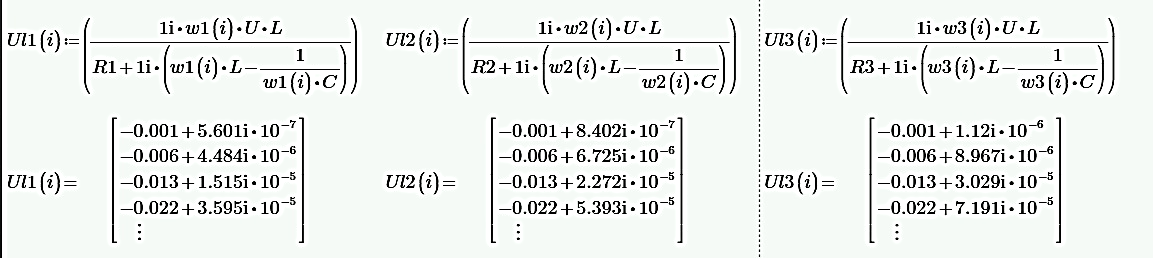 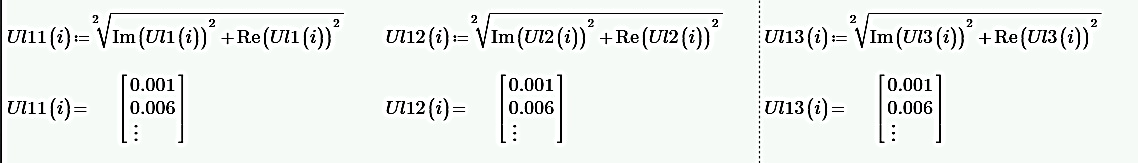 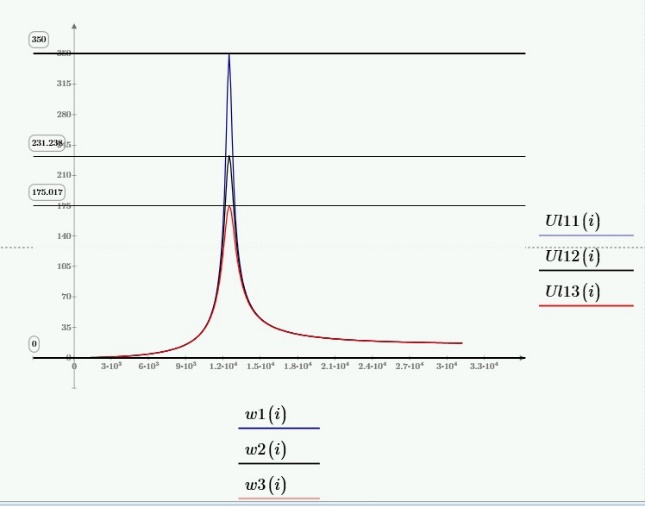 Рис.10 график зависимости напряжения элемента индуктивности контура от рабочей частоты источника ЭДС при разной добротности выводы по разделу Добротность показывает, во сколько раз в резонансном режиме напряжение на индуктивном элементе превышает напряжение на входе цепи. На графике 3 продемонстрирована данная зависимость. С увеличением сопротивление уменьшается добротность и пик напряжения индуктивного элемента. Выводы по работе. В проделанной лабораторной работы были изучены явления резонанса токов (резонанс в параллельном контуре) и напряжений (резонанс в последовательном контуре) в линейной электрической цепи, экспериментально выявлен и доказан резонансный режим работы цепи с помощью графиков, проведены теоретические расчеты резонансной частоты. Изучены экспериментальные зависимости характеристик колебательного контура от рабочей частоты источника ЭДС при резонансе токов и напряжений. Исследован и обоснован характер зависимости напряжения на реактивном элементе от добротности контура при различных активных сопротивлениях. Построены схемы, с помощью программы EWB, для их изучения, и осциллограммы сигналов на входе, для определения резонанса. Отображена зависимость напряжения на одном из реактивных элементов от рабочей частоты источника ЭДС. Рассчитана добротность резонансного контура изменяющиеся от значения активного элемента, и построен график, показывающий во сколько раз в резонансе напряжение на реактивном элементе, превышает напряжение на входе. |
