Отчет 6 лаба ТИСД. Отчет по лабораторной работе 6 обработка деревьев, хешфункций
 Скачать 79.62 Kb. Скачать 79.62 Kb.
|
ФАКУЛЬТЕТ Информатика и системы управления КАФЕДРА Программное обеспечение ЭВМ и информационные технологии ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №6 «ОБРАБОТКА ДЕРЕВЬЕВ, ХЕШ-ФУНКЦИЙ» Студент Козлова Ирина Васильевна Группа ИУ7 – 32Б 2020г. Оглавление Цель работы 2 Описание условия задачи 3 Описание структуры данных 4 Описание алгоритма 6 Набор тестов 6 Оценка эффективности 8 Ответы на контрольные вопросы 10 Вывод 13 Цель работыЦель работы –построить дерево, вывести его на экран в виде дерева, реализовать основные операции работы с деревом: обход дерева, включение, исключение и поиск узлов, сбалансировать дерево, сравнить эффективность алгоритмов сортировки и поиска в зависимости от высоты деревьев и степени их ветвления; построить хеш-таблицу и вывести ее на экран, устранить коллизии, если они достигли указанного предела, выбрав другую хеш-функцию и реструктуризировав таблицу; сравнить эффективность поиска в сбалансированных деревьях, в двоичных деревьях поиска(ДДП),в хеш-таблицахи в файлах. Сравнить эффективность реструктуризации таблицы для устранения коллизий и поиска в ней с эффективностью поиска в исходной таблице. Описание условия задачиПостроить ДДП,сбалансированное двоичное дерево (АВЛ) и хеш-таблицу по указанным данным. Сравнить эффективность поиска в ДДП в АВЛ деревеи в хеш-таблице (используя открытую или закрытую адресацию)и в файле. Вывести на экран деревья и хеш-таблицу. Подсчитать среднее количество сравнений для поиска данных в указанных структурах. Произвести реструктуризацию хеш-таблицы, если среднее количество сравнений больше указанного. Оценить эффективность использования этих структур (по времени и памяти) для поставленной задачи. Оценить эффективность поиска в хеш-таблице при различном количестве коллизий. Описание технического задания В текстовом файле содержатся целые числа. Построить ДДП из чисел файла. Вывести его на экран в виде дерева. Сбалансировать полученное дерево и вывести его на экран. Построить хеш-таблицу из чисел файла. Использовать закрытое хеширование для устранения коллизий. Осуществить добавление введенного целого числа,если его там нет, в ДДП, в сбалансированное дерево, в хеш-таблицу и в файл.Сравнить время добавления, объем памяти и количество сравнений при использовании различных(4-х)структур данных. Если количество сравнений в хеш-таблице больше указанного(вводить),то произвести реструктуризацию таблицы, выбрав другую функцию. Входные данные: Целое число, представляющее собой номер команды: целое число в диапазоне от 0 до 6. Командно-зависимые данные: целочисленные значения (количество элемента стека) Выходные данные: Результат выполнения определенной команды. Сообщение об ошибке. Функции программы: Загрузить данные из файла. Вывести деревья и хеш-таблицу. Добавить элемент. Вывести сравнение. Рассчитать средние величины. 0. Выход из программы. Обращение к программе: Запускается через терминал. Так же можно собрать программу используя makefile, и запустить ее с помощью команды run. Аварийные ситуации: 1. Некорректный ввод номера команды. На входе: число, большее чем 6 или меньшее, чем 0. На выходе: сообщение «ERROR!!! Invalid command entered, please re-enter!!!» 2. Некорректный ввод номера команды. На входе: пустой ввод. На выходе: сообщение «Invalid command entered, please re-enter!!!» 3. Некорректный ввод численных значений требуемых програмой. На входе: пустой ввод/буква. На выходе: сообщение «ERROR!!! Invalid command entered, please re-enter!!!» 4. Некорректный выбор команды. На входе: команда 2 или 4, без вызова команды 1. На выходе: сообщение «ERROR!!! Invalid number input! Please choose some command!» Описание структуры данныхСтруктура, описывающая узел дерева. typedef struct node { int data; unsigned char height; struct node* left; struct node* right; } node_t; Поля структуры data – данные, хранящиеся в узлах height – высота дерева в этом узле *left – указатель на левую ветку дерева *right – указатель на правую ветку дерева Структура, описывающая данные, которые хранятся в таблице. typedef struct { int flag; int value; } intt; Поля структуры flag – знак того, что даная ячейка хеш-таблицы занята value – данные в ячейке хеш-таблицы Структура, описывающая хеш-таблицу. typedef struct { intt *data; int limit; int arrsize; int sizeall; } inttable_t; Поля структуры *data - указатель на данные limit – количество коллизий arrsize – текущий размер хеш-таблицы sizeall — наибольший размер хеш-таблицы Хеш — функция: хеш числа в таблице определяется остатком от деления модуля самого числа на размер таблицы key – число, len – размер таблицы.  Описание алгоритмаВыводится меню данной программы. Пользователь вводит номер команды из предложенного меню. Пока пользователь не введет 0 (выход из программы), ему будет предложено вводить номера команд и выполнять действия по выбору. Ре структурирование таблицы производится следующим образом: увеличением размером таблицы в 2 раза. (см приложение 1) Набор тестов
Оценка эффективностиДобавление элемента (в тактах процессора) в таблице представлены средние величины
Память (в байтах)
Оценка количества сравнение (среднее значение кол-ва сравнений на данном кол-ве элементов, начинается добавление с пустого дерева(таблицы и файла)) Считаю среднее значение путем вычесления среднего арифмитического (сумма всех кол-в сравнения при добавлении всех элементов / на кол-во элементов)
Наиболее эффективна хеш-таблица (наименьшее количество сравнений, зависит от выбранной зеш-функции). Сбалансированное дерево эффективнее несбалансированого. Ответы на контрольные вопросы1.Что такое дерево? Дерево – это нелинейная структура данных, используемая для представления иерархических связей, имеющих отношение «один ко многим». Дерево с базовым типом Т определяется рекурсивно либо как пустая структура (пустое дерево), либо как узел типа Т с конечным числом древовидных структур этого же типа, называемых поддеревьями. 2.Как выделяется память под представление деревьев? Способ выделения памяти под деревья определяется способом их представления в программе. C помощью матрицы или списка может быть реализована таблица связей с предками или связный список сыновей. Целесообразно использовать списки для упрощенной работы с данными, когда элементы требуется добавлять и удалять, т. е. выделять память под каждый элемент отдельно. При реализации матрицей память выделяется статически. 3.Какие стандартные операции возможны над деревьями? Основные операции с деревьями: обход дерева, поиск по дереву, включение в дерево, исключение из дерева. Обход вершин дерева можно осуществить следующим образом: сверху вниз (префиксный обход) слева направо (инфиксный обход) снизу вверх (постфиксный обход) 4.Что такое дерево двоичного поиска? Дерево двоичного поиска – это такое дерево, в котором все левые потомки моложе предка, а все правые – старше. Это свойство называется характеристическим свойством дерева двоичного поиска и выполняется для любого узла, включая корень. С учетом этого свойства поиск узла в двоичном дереве поиска можно осуществить, двигаясь от корня в левое или правое поддерево в зависимости от значения ключа поддерева. 5.Чем отличается идеально сбалансированное дерево от АВЛ дерева? Идеально сбалансированное дерево : при добавлении узлов в дерево мы будем их равномерно располагать слева и справа, то получится дерево, у которого число вершин в левом и правом поддеревьях отличается не более, чем на единицу. АВЛ-дерево : двоичное дерево называется сбалансированным, если у каждого узла дерева высота двух поддеревьев отличается не более чем на единицу. 6.Чем отличается поиск в АВЛ-дереве от поиска в дереве двоичного поиска? Временная сложность поиска элемента в АВЛ дереве – О(log2n) Временная сложность поиска элемента в дереве двоичного поиска –от О(log2n) до O(n). 7.Что такое хеш-таблица, каков принцип ее построения? Массив, заполненный в порядке, определенным хеш-функцией, называется хеш-таблицей. Функцию, по которой можно вычислить этот индекс. называется хеш-функцией. Принято считать, что хорошей является такая функция, которая удовлетворяет следующим условиям: функция должна быть простой с вычислительной точки зрения; функция должна распределять ключи в хеш-таблице наиболее равномерно. функция должна минимизировать число коллизий 8.Что такое коллизии? Каковы методы их устранения. Коллизия - ситуация, когда разным ключам соответствует одно значение хеш-функции, то есть, когда h(K1)=h(K2), в то время как K1 ≠ K2. Первый метод –внешнее(открытое) хеширование (метод цепочек) В случае, когда элемент таблицы с индексом, который вернула хеш-функция, уже занят, к нему присоединяется связный список. Таким образом, если для нескольких различных значений ключа возвращается одинаковое значение хеш-функции, то по этому адресу находится указатель на связанный список, который содержит все значения. Второй метод - внутреннее (закрытое) хеширование (открытая адресация). Оно, состоит в том, чтобы полностью отказаться от ссылок. В этом случае, если ячейка с вычисленным индексом занята, то можно просто просматривать следующие записи таблицы по порядку (с шагом 1), до тех пор, пока не будет найден ключ K или пустая позиция в таблице. 9.В каком случае поиск в хеш-таблицах становится неэффективен? Поиск в хеш-таблицах становится менее эффективен, если наблюдается большое число коллизий. Тогда вместо ожидаемой сложности О(1) получим сложность O(n). В первом методе - поиск в списке осуществляется простым перебором, так как при грамотном выборе хеш-функции любой из списков оказывается достаточно коротким. Во втором методе – необходимо просматривать все ячейки, если есть много коллизий. 10.Эффективность поиска в АВЛ деревьях, в дереве двоичного поиска и в хеш-таблицах Хеш-таблица - от О(1) до O(n) АВЛ-дерево - О(log2n) Дерево двоичного поиска – от О(log2n) до O(n). ВыводОсновным преимуществом деревьев является возможная высокая эффективность реализации основных на ней алгоритмов поиска и сортировки. При удалении или добавлении элемента необходимо корректировать балансировку, тем самым это занимает время. Хеш-таблицы используют меньше памяти, и для них требуется меньшее количество операций сравнения при добавлении. Так же таблицы требуют качественной хеш-функции, чтобы избежать большого количества коллизий. Из переведенной выше оценки эффективности можно сделать вывод, что лучше всего и по памяти и по времени работает хеш-таблица. Это объясняется тем, что для того, чтобы в сбалансированное бинарное дерево добавь элемент, необходимо так де сделать балансировку, что занимает время. Так же, когда мы храним банные в таблице, мы не используем указатели, как в случае с деревьями, поэтому память у хеш-таблицы меньше. Так же можно заметить, что сбалансированное дерево не всегда выигрывает у несбалансированного. Проигрывает во времени, так как порядок вершин всегда меняется, но выигрывает в сравнении (по среднему количеству сравнений добавления), так как высота сбалансированного дерева будет меньше или такой же как и у несбалансированного, поэтому чтобы понять куда надо добавить элемент, приходится меньше ходить по дереву. Приложение 1 Для предложенного мною способа выбора другой хеш-функции и ре структурирования таблицы нашелся пример, который показывает, что данная хеш-функция и ее способы замены не эффективны. Поэтому, проведя некий расчет, я нашла способ улучшить мой алгоритм. Вместо увеличения размеров таблицы в 2 раза, я увеличиваю ее в 1.2 раза, тем самым при примере 1 11 21 31 41 51 61 71 81 91 111 121 131 Таблица выглядит следующим образом 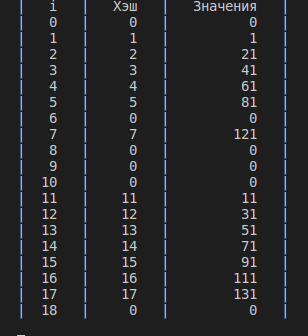 (поле i - идеальное значение хеша, то есть число с таким хешом должно быть записано в данную ячейку, поле Хеш — хеш данного числа) |

