Изучение линейных корректирующих кодов. Отчет по лабораторной работе 7 Изучение линейных корректирующих кодов

• Название: Отчет по лабораторной работе 7 Изучение линейных корректирующих кодов
• Анкор: Изучение линейных корректирующих кодов
• Дата: 25.12.2020
• Размер: 1.02 Mb.
• Имя файла: Mulina_laba7.docx
• Тип: Отчет; #164344

Нижегородский государственный технический университет
им. Р.Е. Алексеева


Кафедра «Электроника и сети ЭВМ»

Отчет по лабораторной работе №7

«Изучение линейных корректирующих кодов»

Выполнил:
Студент группы 17-ОСС
Мулина Е.М.
Проверил:
Семашко А.В.

г. Нижний Новгород

2020 г.

Цель работы: Исследование алгоритмов кодирования и декодирования сообщений с помощью линейных кодов и изучение способов их технической реализации.


Теоретическая часть.
Дискретный канал.



Рис.1. Схема система передачи данных.
В современной теории связи под каналом понимается среда распространения сигнала и совокупность технических средств, предназначенных для передачи информации, которые не могут быть изменены в рамках решаемой задачи. Если структура модулятора и демодулятора заданы, то каналом является та часть линии связи, которая на рис.1 обведена пунктиром. На вход такого канала подаются дискретные кодовые символы αА из некоторого алфавита А, объемом q, а с выхода снимаются символы βА, вообще говоря, не совпадающие с α. Такой канал называется дискретным.
Во всех реальных линиях связи дискретный канал содержит внутри себя непрерывный канал, на вход которого подаются сигналы S(t), а с выхода снимаются искаженные сигналы U(t). Свойства непрерывного канала и характеристики модулятора и демодулятора однозначно определяют все параметры дискретного канала. Иногда дискретный канал называют дискретным отображением непрерывного канала.
Искажения сигнала возникают в результате действия различных помех n(t), действующих в непрерывном канале.
При изучении передачи сообщений по дискретному каналу основной задачей является отыскание методов кодирования и декодирования, позволяющих наилучшим образом передавать информацию в рамках выбранного критерия оптимальности.

Помехоустойчивое кодирование.
Помехоустойчивое кодирование - процесс преобразования информации, предоставляющий возможность обнаружить и исправить ошибки, возникающие при передаче информации по каналам передачи данных.
Под ошибкой при этом понимают ситуацию, когда в результате действия помех и искажений в канале передачи данных приемник принимает неверное решение, отождествляя принятый сигнал не с фактически переданным символом, а с каким-либо другим.
Процесс помехоустойчивого кодирования заключается во введении избыточности, т. е. для передачи информации используется код, у которого используются не все возможные комбинации, а только некоторые из них. Такие коды называют избыточными или корректирующими.
Соответственно, процесс введения избыточности (преобразование информационных символов в кодовое слово) называется кодированием, а обратный процесс восстановления информации из кодового слова, возможно содержащего ошибки, - декодированием.
Основными параметрами, характеризующими корректирующие свойства кодов являются:

1. 
   избыточность кода;
   

2. 
   кодовое расстояние;
   

3. 
   кратность гарантированно обнаруживаемых ошибок;
   

4. 
   кратность гарантированно исправляемых ошибок.
   

Под избыточностью понимают число вводимых дополнительных разрядов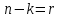

где n — число кодовых символов на выходе кодера, соответствующих k информационным символам на его входе.
Кодовое расстояние d или расстояние характеризует степень различия любых двух кодовых комбинаций. Оно выражается числом разрядов, в которых комбинации отличаются одна от другой.



Для помехоустойчивого кода наиболее важным является минимальное кодовое расстояние - наименьшее кодовое расстояние из всех между всеми парами кодовых комбинаций.
В общем случае при необходимости обнаруживать ошибки кратности минимальное кодовое расстояние должно быть, по крайней мере, на единицу
больше , т. е.
Соответственно, кратность гарантированно обнаруживаемых кодом ошибок равна



Кратность гарантированно исправляемых кодом ошибок вычисляется по формуле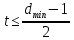



Таким образом, код, имеющий минимальное кодовое расстояние ,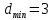

позволяет гарантированно обнаружить 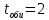и менее ошибок и гарантированно
исправить t = 1 ошибку.
Коды коррекции ошибок.
Линейными или групповыми кодами коррекции ошибок называются методы реализации помехоустойчивого кодирования.
Линейные блочные коды позволяют представить информационные и кодовые слова в виде двоичных векторов, что позволяет описать процессы кодирования и декодирования с помощью аппарата линейной алгебры, с учетом того, что компонентами вводимых векторов и матриц являются символы «0» и «1». Операции над двоичными компонентами производятся при этом по правилам арифметики по модулю 2.
Множество 2k возможных двоичных информационных слов блокового (n,k)-кода взаимно однозначно отображается в множество 2k кодовых слов длиной n.
Рассмотрим механизм исправления и обнаружения ошибок в помехоустойчивом кодировании. Для этого удобно рассмотреть множество двоичных слов (векторов) длиной n в виде точек на плоскости (см. рис. 2).
На рис. 2 черными кругами показаны два кодовых слова 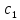, ,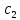 отличающиеся друг от друга в двоичных символов. Вокруг них показаны области, содержащие слова длиной n, отличающиеся от этих кодовых слов не более чем в t позициях. Прочие кодовые слова показаны черными ромбами.

Рис.2. Общий принцип исправления и обнаружения ошибок.

В случае, если по каналу было передано кодовое слово , и оно пришло с искажениями, возможны три варианта декодирования с исправлением ошибки.
1. Было получено слово, попадающее в область вокруг вектора 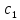. Такое слово будет преобразовано декодером в слово 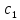и декодирование будет осуществлено верно.

2. 
   Если получено слово, не принадлежащее областям ни одного кодового слова, то оно не может быть декодировано и, следовательно, возникает ошибка декодирования.
   

3. Слово, попадающее в область вокруг 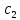, будет преобразовано декодером в .
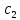Такая ошибка не может быть обнаружена.
В показанном на рис. 5.1 случае не все слова размерности n принадлежат областям декодирования. Таких кодов большинство. Коды, в которых непересекающиеся области декодирования охватывают все пространство слов размерности n, называются совершенными или плотноупакованными. При использовании совершенных кодов всегда возможна коррекция ошибок (не всегда правильная). Декодер такого кода не может определить ошибку декодирования. Он работает либо в режиме определения ошибок, либо в режиме исправления ошибок. Основными совершенными кодами являются коды Хэмминга и коды Голея.
Код Хэмминга можно построить для любого натурального числа r ≥ 3. Этот код будет обладать рядом свойств.

1. 
   n=2r-1
   
2. 
   k=2r-1-r
   
3. 
   r=n-k
   
4. 
   d_min=3, t=1
   

Кодирование линейных блочных кодов.
Поскольку между информационными и кодовыми словами существует взаимно однозначное соответствие, процесс кодирования может быть осуществлен с использованием таблицы соответствий, хранящейся в памяти кодера. Однако, для длинных кодов такой метод неприемлем, так как требует большой объем памяти для хранения таблицы.
Вместо этого вводится понятие так называемой порождающей матрицы G. Оно основано на том, что подпространство всех кодовых слов линейного блочного (n,k) -
кода имеет некоторый базис (v0,v1,…,vk-1 ), через который может быть выражено любое кодовое слово этого кода.

v=u₀v₀+u₁v₁+…+u_k-1v_k-1, (1)

где .

Векторы базиса образуют порождающую матрицу G размера



Тогда уравнение (1) принимает вид

v=uG(2)

где u=(u₀,u₁, u_k-1) - информационное слово.
Фактически, формула (36) описывает процедуру кодирования линейного блочного кода посредством образующей матрицы. Для пространства кодовых слов линейного (n,k)-кода существует дуальное ему пространство кода (n,n−k), порождаемое матрицей H размера (n−k)×n. Такая матрица получила название проверочной для кода (n,k) и обладает следующими свойствами
GH^T=0 (3)

vH^T=0

на основе которых реализована операция декодирования линейных блочных кодов.
Как правило рассматривают так называемые систематические или каноничные формы матриц G и H, использующиеся для процедуры систематического кодирования. На практике, любая порождающая матрица G линейного блочного (n,k)-кода может быть преобразована к систематическому виду посредством элементарных операций и перестановок столбцов матрицы.
Матрица G в систематической форме состоит из двух подматриц: единичной матрицы I размера k×k и проверочной подматрицы P размера k×(n−k) .


Соответственно, исходя из свойства (3), следует, что проверочная матрица H состоит из транспонированной проверочной матрицы и единичной матрицы размера .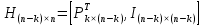


Декодирование линейных блочных кодов.
Как и в случае кодирования, декодирование линейных блочных кодов можно осуществлять посредством таблицы по принципу максимального правдоподобия. В этом случае производится последовательное поразрядное сравнение принятого на вход декодера слова со всеми возможными кодовыми словами. В результате будет выбрано кодовое слово, имеющее наименьшее число отличий от декодируемого. В случае несовершенных кодов возможен вариант, когда есть несколько кодовых слов, отличающихся от принятого в одинаковом числе разрядов. Соответственно, декодер

не может принять решение о верности одного из вариантов и выдает сигнал о невозможности декодирования. Недостатки такой схемы те же, что и в случае кодирования - необходим большой объем памяти для хранения всех кодовых слов в случае длинных кодов. Быстродействие для длинных кодов также значительно увеличивается.
В связи с этим используют механизм синдромного декодирования, основанный на использовании проверочной матрицы H.
Для понимания принципа декодирования рассмотрим как выражаются проверочные символы кодового слова через информационные на примере систематического кода Хэмминга (7,4).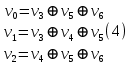



Если в канале произошла ошибка, то для принятого вектора r хотя бы одно из равенств (4) выполняться не будет. Проверочные соотношения можно записать для принятого вектора в виде системы уравнений (4).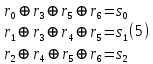



Соответственно, если хотя бы один из компонент вектора s = { 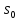, , 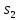} не равен нулю, то в принятом слове есть ошибка.
Уравнения (5) можно записать через проверочную матрицу H.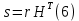



Вектор s принято называть синдромом. Таким образом, ошибка в принятом слове будет обнаружена, если хоть один компонент синдрома принятого слова не равен нулю. Для исправления ошибки используется тот факт, что каждый синдром соответствует своей позиции одиночной ошибки (мы говорим о кодах Хэмминга).
Расширенные коды Хэмминга.
Расширение кода Хэмминга заключается в дополнении кодового слова дополнительным двоичным разрядом так, чтобы оно содержало четное число единиц. Такое расширение дает ряд преимуществ.

1. 
   Длина кода увеличивается до n = 2r, что удобнее для хранения и передачи информации.
   

2. Минимальное расстояние = 4, следовательно 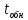= 3.
Также, дополнительный разряд позволяет использовать декодер в гибридном режиме обнаружения и коррекции ошибок.

Практическая часть.
Техническое задание: Написать программу для реализации кодирования и декодирования помехоустойчивым кодом Хемминга.
Исходные данные:
Порождающая матрица G: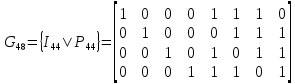



Проверочная матрица H: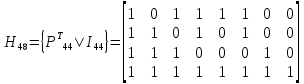



Текст для кодирования:
One of the most alarming forms of air pollution is acid rain. It results from the release into the atmosphere of sulphur and nitrogen oxides that react with water droplets and return to earth in the form of acid rain, mist or snow.
Acid rain is killing forests in Canada, the USA, and central and northern Europe. (Nearly every species of tree is affected.) It has acidified lakes and streams and they can’t support fish, wildlife, plants or insects. (In the USA 1 in 5 lakes suffer from this type of pollution).

Листинг программы.
























Результаты работы программы.


Рис.3. Интерфейс программы.



Рис.4. Результаты кодирования.


Смоделируем действие шума в двоичном канале, изменив произвольным образом N символов:

Шифр до внесения изменений:
01000111 11111111
01101100 11100010
01101100 01011010
00101011 00000000
01101100 11111111
01101100 01101100
00101011 00000000
01110001 01000111
01101100 10001110
01101100 01011010

Шифр после внесения изменений:
01001111 11111111
01101100 11100010
11101100 01011010
00101011 00010000
01101100 11111111
01101000 01101100
00101011 00000000
01110001 11010111
01101100 10001110
01101101 01011010

Из рис.5 видно, что при декодировании по синдрому можно однозначно определить расположение единичной ошибки в пакете и сразу же исправить еѐ, и обнаружить наличие двойной, неисправимой ошибки.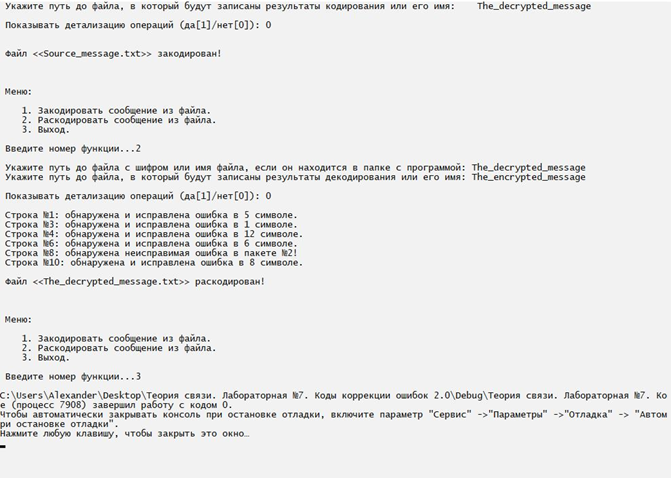


Рис.5.



Рис.6. Результаты декодирования.


Вывод:
В ходе данной лабораторной работы мы изучили коды коррекции ошибок Хэмминга. Этот метод позволяет за счет избыточного кодирования шифровать информацию в двоичной системе перед её передачей через непрерывный канал, в котором сообщение может частично исказиться, так, чтобы ошибки, возникшие при передаче, не привели к потере информации или её неверной интерпретации.

Написанная программа реализует шифрование расширенным (8,4) - кодом Хэмминга с параметрами: число информационных символов k =4, избыточность r=4 , минимальное кодовое расстояние d_min = 3, кратность гарантированно исправляемых кодом ошибок t_обн = 2, кратность обнаруживаемых кодом ошибок t=1. Результаты работы программы полностью подтверждают автокорректирующие и автоконтролирующие свойства кода Хэмминга.