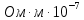7лаб. Отчет по лабораторной работе 7 По дисциплине
 Скачать 251.33 Kb. Скачать 251.33 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра общей и технической физики Отчет по лабораторной работе №7 По дисциплине ФИЗИКА Тема: Измерение сопротивлений при помощи моста Уитстона Выполнил: студент группы ГС-21-1 ___________ Шумер А.В. (подпись) (Ф.И.О.) Дата:  Проверил: ____________ Проверил: ____________ (должность) (подпись) (Ф.И.О.) Санкт-Петербург 2022 Цель работы: 1. Изучение принципа работы измерительной мостовой схемы Уитстона. 2. Определение сопротивления проволочных проводников. 3. Определение удельного сопротивления материала. Краткое теоретическое содержание Явление, изучаемое в работе: электрическое сопротивление Одинарный измерительный мост постоянного тока впервые был предложен в 1833 г. Этот способ измерения отличает более высокая точность, т. к. он основан на сравнении измеряемой величины с ее эталоном или образцовой мерой. Поэтому он может быть применен для поверки и градуировки электроизмерительных приборов. Основной частью электрической цепи моста Уитстона является четырехполюсник, т. е. участок цепи, имеющий четыре узла (полюса). Измеряемое сопротивление 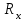 и три других сопротивления образуют замкнутый четырехугольник. В одну диагональ четырехугольника включен гальванометр G (этот участок и является мостиком), а в другую диагональ включен источник постоянного тока с ЭДС, равной ɛ. и три других сопротивления образуют замкнутый четырехугольник. В одну диагональ четырехугольника включен гальванометр G (этот участок и является мостиком), а в другую диагональ включен источник постоянного тока с ЭДС, равной ɛ.Гальванометром называется электроизмерительный прибор, имеющий высокую чувствительность к току или напряжению. 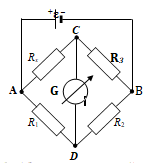 Рис. 1. Электрическая схема моста Уитстона На практике очень часто используют схему так называемого линейного или реохордового моста Уитстона (см рис.1). Сопротивления R1 и R2 в этой схеме лежат на одной прямой и вместе представляют собой однородную проволоку (реохорд), по которой на скользящем контакте перемещается движок D, соединенный с гальванометром G. Одинарные мосты постоянного тока по схеме Уитстона находят широкое применение для измерения сопротивлений от 1 до 1010 Ом. В некоторых случаях их диапазон может быть расширен до 10-4 и 1015 Ом. Правда, при измерении очень больших сопротивлений инструментальная погрешность может превышать 10%. Промышленность выпускает приборы, работающие по мостовой схеме Уитстона, в которых процесс измерения проводится в автоматическом или полуавтоматическом режиме и результат выводится в виде цифр на индикаторном табло (рис. 2).  Рис. 2. Промышленный мост Уитстона Для измерения малых сопротивлений от 1 мкОм до 1 Ом применяют двойные или многоплечные мосты. Также находят применение комбинированные одинарно-двойные мосты, позволяющие измерять сопротивления от 1 мкОм до 1 МОм с погрешностью 0,002%. Виды мостовых схем Одинарные мосты на переменном токе Одинарные мосты могут работать также и на переменном токе. Обобщенная электрическая схема такого моста изображена на рис. 3. В этом случае сопротивления плеч являются комплексными величинами. Индикатором нуля в такой схеме обычно служит электронный милливольтметр. В некоторых случаях в качестве электронного индикатора нуля может выступать электроннолучевая трубка осциллографа. Электронные индикаторы имеют очень большое входное сопротивление, что выгодно отличает их от электромеханических устройств, например, гальванометра.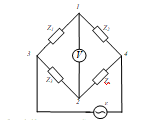 Рис.3. Схема измерительного моста переменного тока В качестве регулируемых элементов в таких схемах могут выступать резисторы и конденсаторы, т. к. они допускают более тонкую регулировку, чем катушки индуктивности. Поскольку результаты измерения емкости и индуктивности зависят от частоты питающего мост напряжения источника, измерения проводят при заданной частоте. Равновесие моста переменного тока обычно добиваются регулировкой не одного, а двух элементов. Наиболее распространенные измерительные мосты переменного тока работают на сетевой частоте (50…60) Гц, либо на звуковых частотах вблизи 1 кГц. Мост Максвелла-Вина Для точных измерений индуктивности и добротности катушек используется мост Максвелла-Вина, изображенный на рис. 4. Такой мост позволяет производить сравнение эталонной катушки с эталонными емкостями в случае неизвестной рабочей частоты. Использование эталонных емкостей оказывается гораздо выгоднее, поскольку емкости проще по конструкции, чем катушки; их легче экранировать, и они не создают внешних электромагнитных полей. Последнее обстоятельство является критически важным, т. к. измерительные мосты необходимо тщательно заземлять и экранировать, чтобы паразитные емкости между разными частями схемы не вносили ошибку при достижении равновесия моста. 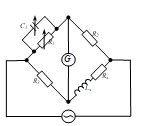 Рис.4. Схема моста Максвелла-Вина Преимущество мостовой схемы Максвелла-Вина в том, что она позволяет получить равновесие, даже если в сигнале источника питания присутствуют дополнительные гармоники с частотами, отличными от рабочей частоты, если величина 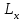 не зависит от частоты. не зависит от частоты. Законы и соотношения, использованные при выводе расчётных формул Закон Ома для участка цепи: 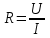 . .Формула расчёта сопротивления через удельное сопротивление: 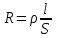 Схема установки 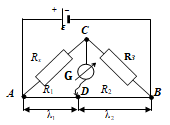 G — гальванометр ABCD — четырёхполюсник АВ = λ1+ λ2 — реохорд R1, R2, R3 — резисторы с известным сопротивлением Rx — резистор с неизвестным сопротивлением ε — ЭДС источника Основные расчётные формулы 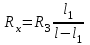 , где , гдеRx — неизвестное сопротивление, Ом R3 — одно из известных сопротивлений, Ом l — полная длина реохорда, м l1 — левое плечо реохорда, м 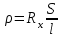 , где , гдеρ — удельное сопротивление проводника, Ом·мм²/м S — площадь поперечного сечения проводника, мм2 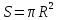 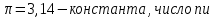 R – радиус проводника, м Формулы для расчёта погрешностей косвенных измерений 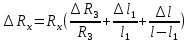 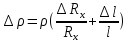 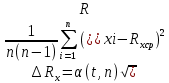 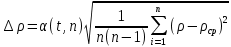 Таблица №1. Зависимость сопротивления от длин плеч реохорда
Таблица №3 Зависимость удельного сопротивления от длин плеч реохорда
Таблица №2. Зависимость сопротивления от длин плеч реохорда и диаметра проволоки
Примеры вычислений Исходные данные: d1 = 1 мм d2 = 0,7 мм d3 = 0,5 мм 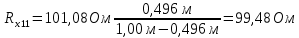 S1 = 3,14 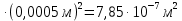 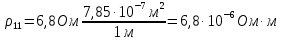 Косвенная погрешность для таблицы №1: 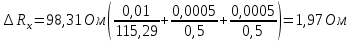 Абсолютная погрешность для таблицы №1: 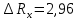 Ом ОмКосвенная погрешность для таблицы №2: 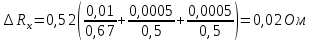 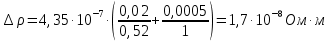 Абсолютная погрешность для таблицы №2: 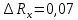 Ом Ом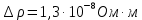 Косвенная погрешность для таблицы №3: 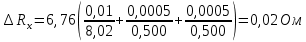 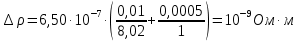 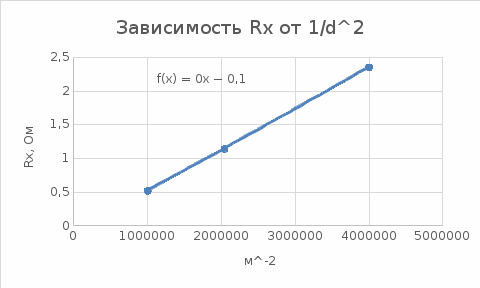 Рис.5. Зависимость сопротивления Rx от обратного d2 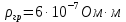 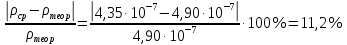 Вывод В ходе выполнения лабораторной работы определено, что экспериментальное значение удельного сопротивления проволоки из константана близко к теоретическому значению удельного сопротивления данного материала. Расхождение с теоретическими данными составило 11,2%. Данное расхождение обусловлено прямыми и косвенными погрешностями измерений. Следовательно, с помощью моста Уинстона можно с большой точностью определить сопротивление того или иного материала. |