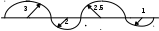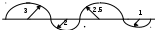1)
|
Определите периметры правильных n – угольников (10 – угольника, 50 – угольника, 100 – угольника), вписанных в окружность заданного радиуса R.
Сторона правильного n-угольника  периметр n-угольника 
|
2)
|
Определите длины всех медиан треугольника, заданного длинами сторон a,b,c.
Медиана, проведенная к стороне a: 
|
3)
|
Определите углы между тремя векторами, направленными из общей начальной точки с координатами (0,0) в конечные точки: точку (2;5); точку (7;6); точку (9;3).
Угол между 2-мя векторами, проведенными из точки (0, 0) в точки (x1, y1) и (x2, y2) вычисляется по формуле 
|
4)
|
Вычислите площадь пятиугольника, заданного прямоугольными координатами своих вершин: A1(3;2), A2(9;6), A3(14;2), A4(10;-3), A5(7;-2)
Использовать формулу площади треугольника:
|
5)
|
Определите длины всех биссектрис треугольника, заданного длинами сторон a, b, c. Биссектриса угла  вычисляется по формуле
|
6)
|
Вычислите R – расстояние между двумя точками A и B, заданными сферическими координатами. Соотношение между сферическими координатами и декартовыми
|
7)
|
Вычислите значение площади полной поверхности треугольной пирамиды, если известны длины всех ребер:
|AB| = 3; |AD| = 5; |DB| = 4; |DC| = ; |BC| = ; |AC| = 5.
Для вычисления площади треугольника использовать формулу Герона: , где a, b, c - длины сторон треугольника.
|
8)
|
Определите высоту, на которой будет мяч, подброшенный вертикально вверх с высоты y0=1м и начальной скоростью V0=20м/сек через время t=1сек, 3сек и 4сек. Высота в момент t  , где  м/сек
|
9)
|
Определите площади правильных n - угольников (10-угольника; 50-угольника; 100-угольника), вписанных в окружность радиуса R
Сторона правильного n-угольника
 - радиус вписанной окружности;
площадь n-угольника 
|
10)
|
Определите площадь кольца, внутренний радиус которого равен R1; а внешний R2 (R2>R1). Площадь круга радиуса R вычисляется по формуле:
|
11)
|
Вычислите полярные координаты 3-х точек, заданных прямоугольными координатами в правой полуплоскости. Формулы преобразования координат: .
|
12)
|
Определите площадь каждого из 3-х секторов с радиусами R1, R2, R3 и с центральными углами 
Площадь сектора радиуса R c центральным углом (в градусах) равна  .
|
13)
|
Вычислите 
|
14)
|
Определите стороны треугольника, заданного величинами своих углов и радиусом описанной окружности.
Применить теорему синусов
 
|
15)
|
Определите площадь каждого из 3-х кругов, ограниченных тремя окружностями, длины которых L1, L2 ,L3 известны.
Площадь круга  длина окружности 
|
16)
|
Определите углы треугольника, длины сторон которого a, b, c заданы.
Примените теорему половинного угла
 где  угол, противолежащий стороне с
|
17)
|
Вычислите 
|
18)
|
Определите общую длину дуги, образованной полуокружностями
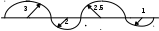
Длина половины окружности 
|
19)
|
Вычислите стороны треугольника A и B при условии, что заданы сторона C и углы треугольника и  .
Сторона треугольника вычисляется по формуле  ,где - угол, противолежащий стороне A,  - угол, противолежащий стороне C
|
20)
|
Вычислите значения медиан треугольника, сторонами которого являются медианы исходного треугольника со сторонами a, b, c.
Длина медианы, проведенной к стороне a: 
|
21)
|
Вычислите 
|
22)
|
Вычислите 
|
23)
|
Определите длину дуги каждого из трех секторов с радиусами R1, R2, R3 и с центральными углами
Длина дуги сектора радиуса R c центральным углом (в градусах) равна 
|
24)
|
Вычислите координаты точки пересечения двух прямых:
 , вычисляемые по формулам: , где  .
|
25)
|
Вычислите 
|
26)
|
Определите все углы треугольника при заданных значениях сторон a, b, c.
Угол, лежащий против стороны a, вычисляется по теореме косинусов:
|
27)
|
Вычислите определенный интеграл  для функции 
по приближенной формуле Симпсона
|
28)
|
Вычислите площади трех кругов S1, S2 и S3 с заданными диаметрами d1, d2 и d3 по формуле:
|
29)
|
Вычислите 
|
30)
|
Определите общую площадь фигуры, образованной полукругами
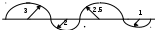
Площади полукруга  .
|
Скачать 362.5 Kb.