Лаб_Вращ.Обербека-Адиабата-Мостик. Отчет по лабораторной работе по физике факультет Электротехникаэлектроэнергетика
 Скачать 313.92 Kb. Скачать 313.92 Kb.
|
|
ОПИСАНИЕ УСТАНОВКИ Схема установки представлена на рисунке 2. В сосуд насосом накачивают воздух, создавая давление выше атмосферного. Это состояние газа соответствует началу эксперимента, на графике (рис.3) это точка 1. При этом газ имеет параметры Р1,V1,T1. 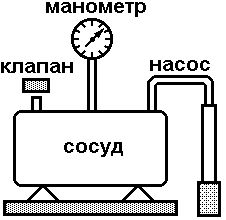 Рис. 2. Схема эксперимен-тальной установки. Быстрое расширение воздуха можно рассматривать как адиабатическое. Поэтому, открывая клапан сосуда на мгновение, в течение которого давление внутри сосуда достигает атмосферного, мы можем считать, что газ перейдет в новое состояние, характеризуемое величинами Р2,V2,T2 по адиабате (точка 2 на рисунке 3). Температура воздуха в сосуде после адиабатического расширения будет ниже начальной. Параметры начального и конечного состояний воздуха в сосуде при адиабатическом процессе связаны уравнением Пуассона (уравнением адиабаты): 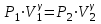 или или 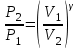 . (14) . (14)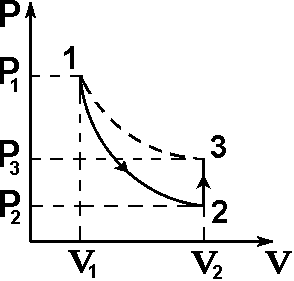 Рис. 3. Диаграмма процессов, происходящих с воздухом в сосуде. Через несколько минут воздух в сосуде нагреется до температуры окружающей среды Т1. Поскольку при этом V2 не изменяется, то давление повысится до Р3. Новое состояние воздуха характеризуется параметрами Р3,V2,T1 (точка 3 на рисунке 3). Сравнивая состояние воздуха в сосуде, соответствующее точкам 3 и 1 (рис.3), видим, что температура воздуха в этих точках одинакова. Тогда по закону Бойля – Мариотта: 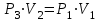 или или 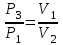 . (15) . (15)Сравнивая уравнения (14) и (15) получим:  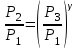 . (16) . (16)Прологарифмировав уравнение (16), получим 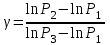 . (17) . (17)Условия эксперимента позволяют упростить формулу (17) следующим образом: 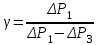 . (18) . (18)ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ЗАДАНИЯ При закрытом клапане накачать воздух в сосуд так, чтобы измеряемое манометром избыточное давление стало равным 100 – 130 мм. рт. ст. Через некоторое время, когда давление перестанет падать записать в таблицу величину давления Р1. Открыть на мгновение клапан сосуда и когда стрелка манометра упадет до нуля быстро закрыть его. Через некоторое время, когда давление перестанет расти, записать величину давления Р3 в таблицу. Повторить пункты 1-3 пять раз. По формуле (18) рассчитать коэффициент Пуассона для каждого опыта. Вычислить среднее значение коэффициента Пуассона ср. Найти теоретическое значение коэффициента Пуассона теор для воздуха, считая его молекулы жесткими двухатомными (указание: воспользоваться определениями коэффициента Пуассона и молярных теплоемкостей при постоянном объеме и давлении). Сравнить теоретическое и среднее экспериментальное значения коэффициента Пуассона, оценив величину относительного отклонения по формуле 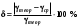 . .Таблица
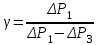 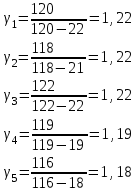 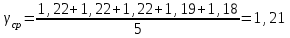 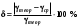 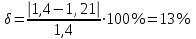 КОНТРОЛЬНЫЕ ВОПРОСЫ Что такое удельная и молярная теплоемкости вещества? От чего они зависят, в каких единицах измеряются? Удельной теплоемкостью вещества называется величина, численно равная количеству теплоты, которое необходимо сообщить веществу единичной массы, чтобы увеличить его температуру на один Кельвин: 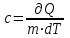 . . Единица удельной теплоемкости в системе СИ – джоуль на килограмм-кельвин: [с] = Дж / (кгК). Молярной теплоемкостью вещества называется величина, численно равная количеству теплоты, которое необходимо сообщить молю вещества, чтобы увеличить его температуру на один Кельвин: 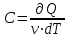 . . Единица молярной теплоемкости в системе СИ – джоуль на моль-кельвин: [С] = Дж / (мольК). Что такое коэффициент Пуассона ? Коэффициент Пуассона равен отношению теплоемкостей 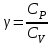 . .Сформулируйте первое начало термодинамики. Согласно первому началу термодинамики, термодинамическая система (например, пар в тепловой машине) может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии. Первое начало термодинамики объясняет невозможность существования вечного двигателя 1-го рода, который совершал бы работу, не черпая энергию из какого-либо источника. Сущность первого начала термодинамики заключается в следующем: При сообщении термодинамической системе некоторого количества теплоты Q в общем случае происходит изменение внутренней энергиисистемы DU и система совершает работу А: Q = DU + A (1) Уравнение (1), выражающее первое начало термодинамики, является определением изменения внутренней энергии системы (DU), так как Q и А — независимо измеряемые величины. Внутреннюю энергию системы U можно, в частности, найти, измеряя работу системы в адиабатном процессе (то есть при Q = 0): Аад = — DU, что определяет U с точностью до некоторой аддитивной постоянной U0: U = U + U0 (2) Первое начало термодинамики утверждает, что U является функцией состояния системы, то есть каждое состояние термодинамической системы характеризуется определённым значением U, независимо от того, каким путём система приведена в данное состояние (в то время как значения Q и А зависят от процесса, приведшего к изменению состояния системы). При исследовании термодинамических свойств физической систем первое начало термодинамики обычно применяется совместно со вторым началом термодинамики. Что такое внутренняя энергия идеального газа? От чего она зависит? Исходя из определения идеального газа, в нем отсутствует потенциальная составляющая внутренней энергии (отсутствуют силы взаимодействия молекул, кроме ударного). Таким образом, внутренняя энергия идеального газа представляет собой только кинетическую энергию движения его молекул. Внутренняя энергия зависит от температуры. Дать определение работы газа и количества теплоты. При расширении газ совершает работу против внешней среды, передавая ей при этом энергию. При сжатии наоборот, газ воспринимает работу, совершенную внешней средой и увеличивающей его внутреннюю энергию. При этом осуществление работы возможно при наличии по меньшей мере двух движущихся тел, одно из которых оказывает силовое воздействие на другое. Из сказанного следует, что работа есть одна из форм передачи энергии от одного тела к другому. Количество работы представляет собой меру передаваемой энергии. Количество энергии, полученное телом в форме работы, называется совершенной над телом работой, а отданную энергию в форме работы – затраченной телом работой. Количество теплоты - энергия, переданная системе внешними телами путем теплообмена (процесс обмена внутренними энергиями при контакте тел с разными температурами). Можно говорить о двух формах передачи энергии от одних тел к другим: работе и теплоте. Энергия механического движения может превращаться в энергию теплового движения и наоборот. При этих превращениях соблюдается закон сохранения и превращения энергии, применительно к термодинамическим процессам этим законом и является первое начало термодинамики, установленное в результате обобщения многовековых опытных данных. ОТЧЕТ ВЫВОДЫ: Результаты экспериментальных расчетов по вычислению коэффициента Пуассона для воздуха приближенно совпадают с истинным значением. Погрешность эксперимента можно считать удовлетворительной. ЛАБОРАТОРНАЯ РАБОТА № 24. ОПРЕДЕЛЕНИЕ СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ МОСТИКОМ УИТСТОНА Цель работы: ознакомиться с принципом работы схемы мостика Уитстона. Определить неизвестное сопротивление и удельное сопротивление проводника. 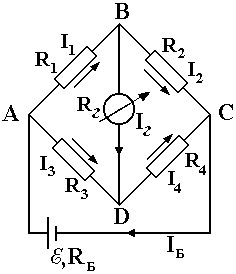 Рис. 2. Схема мостика Уитстона 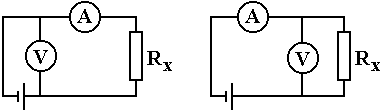 а) б) Рис. 1. Схема определения сопротивления Теоретическое введение. Наиболее часто для измерения сопротивления проводника применяется одна из схем, приведенных на рис. 1 (а и б), в силу их простоты. Однако любая из этих схем обладает существенным недостатком. В самом деле, любой прибор обладает конечным, но не нулевым сопротивлением. Поэтому, даже при высоком классе точности приборов, вольтметр, в первом случае, будет показывать суммарное падение напряжения на амперметре и исследуемом сопротивлении (показания амперметра соответствуют току через RХ). Во втором случае амперметр будет показывать суммарный ток, протекающий через вольтметр и сопротивление RХ. Показания же вольтметра соответствуют падению напряжения на RХ. Таким образом, в любом из этих случаев значение сопротивления RХ, найденное из закона Ома, будет неверным.  а) б) Рис. 1. Схема определения сопротивления.  Рис. 2. Схема мостика Уитсона. Схема, сводящая к минимуму влияние прибора на точность измерений, была предложена Уитстоном - так называемый мостик Уитстона (рис. 2). Четыре сопротивления R1,R2,R3,R4 образуют плечи мостика. RБ и - сопротивление и ЭДС батареи. Rг и Iг - сопротивление гальванометра и ток, протекающий через него. Для расчета сложных цепей, одной из которых является мостик Уитстона, применимы правила Кирхгофа. Первое правило: алгебраическая сумма токов, сходящихся в любой точке разветвленной цепи, равна нулю: 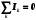 (1). (1).Токи учитываются со знаком «+», если они приходят в рассматриваемую точку, и со знаком «–», если они выходят из этой точки. Первое правило Кирхгофа применяется к узловым точкам цепи, в которых сходятся три и более токов. Первое правило вытекает из закона сохранения электрического заряда. Второе правило: если несколько участков электрической цепи образуют замкнутый контур, то сумма падений напряжений на всех участках этого контура равна сумме ЭДС, действующих в этом контуре: 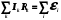 (2). (2).Падение напряжения IR считается положительным, если выбранное направление тока на данном участке контура совпадает с направлением обхода контура и отрицательным, если направление тока и обхода противоположны. ЭДС имеет положительное значение, если при обходе контура внутри элемента переходим от «–» полюса источника к «+», и отрицательное, если наоборот. Воспользовавшись правилами Кирхгофа, можно получить шесть независимых уравнений для мостика Уитстона. По первому правилу Кирхгофа для узлов А, В и С: 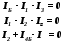 (3) (3)По второму правилу Кирхгофа для контуров АВСА, АВDА и ВСDВ 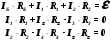 (4) . (4) .Эти уравнения позволяют найти шесть неизвестных величин. Если неизвестно одно из сопротивлений, например R1, то измеряя гальванометром силу тока Iг, из уравнений получают остальные токи и искомое сопротивление R1. Так поступают в случае неравновесного мостика Уитстона. Изменяя сопротивления R2,R3,R4, можно добиться, что ток через гальванометр станет равным нулю. В этом случае гальванометр не внесет искажений в схему, и уравнения (3) примут вид I1 = I2I3 = I4 , из уравнений (4) получим: I1R1 = I3R3 I2R2 = I4R4 , отсюда: 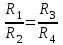 (5) . (5) .Неизвестное сопротивление R1 можно выразить через три других сопротивления 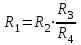 (6) . (6) .Равенство нулю силы тока через гальванометр определяет равновесное состояние мостика Уитстона. В этом случае, как видно из формулы (6), для вычисления неизвестного сопротивления необходимо знать абсолютное значение сопротивления R2 и отношение R3/R4. ОПИСАНИЕ УСТАНОВКИ 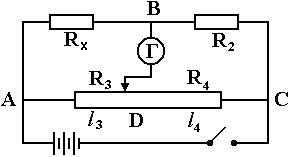 |
