Лаб_Вращ.Обербека-Адиабата-Мостик. Отчет по лабораторной работе по физике факультет Электротехникаэлектроэнергетика
 Скачать 313.92 Kb. Скачать 313.92 Kb.
|
|
По данным таблицы 1 строится график зависимости углового ускорения от момента силы тяжести опускающегося груза mgr, т.е. ε=f(mgr). Отрезок, отсекаемый прямой на оси моментов сил, равен моменту сил трения, возникающему при трении шкива об ось. Проверка второй зависимости (8) осуществляется путем выполнения второй серии опытов. Для этого перепишем соотношение (12) в виде 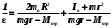 . (15) . (15)При постоянной массе m груза второе слагаемое, а также знаменатель первого слагаемого в выражении (15) остаются постоянными. Таким образом, величина 1/ должна быть пропорциональна изменяющемуся моменту инерции грузов 2mοR2. Величину 1/ находят в соответствие с (14) по формуле: 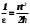 . .Массу груза m на нити установить равной 102 г. Момент инерции грузов меняется за счет изменения расстояния R грузов m0 до оси вращения в соответствии с таблицей 2, в которую так же вносятся результаты измерений и расчетов. Таблица 2
По данным таблицы 2 строится график зависимости 1/ от переменного момента инерции 1/ε=f(2mοR2). Отрезок, отсекаемый графиком на оси моментов инерции, равен моменту инерции маятника без грузов m0 , то есть моменту инерции шкива и спиц. По данным приборов определяют систематические погрешности tсист и hcист. Поскольку высота, с которой опускается груз каждый раз задается одинаковым образом, то можно считать, что hсл=0. Случайная погрешность в определении времени находится обычным образом по трем измерениям. Полная погрешность находится по формуле t =tcист+tсл. Погрешность r можно положить равной 1 мм. Погрешности в определении углового ускорения рассчитываются по формулам: 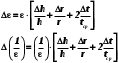 . (16) . (16)Выражение, стоящее в квадратных скобках, следует рассчитать один раз для средней строки одной из таблиц и использовать это значение для расчета погрешностей и -1 в каждой строке таблиц 1 и 2. По результатам работы сделать соответствующие выводы. КОНТРОЛЬНЫЕ ВОПРОСЫ Записать и объяснить основной закон динамики вращательного движения. Дать определения величин, входящих в это уравнение. 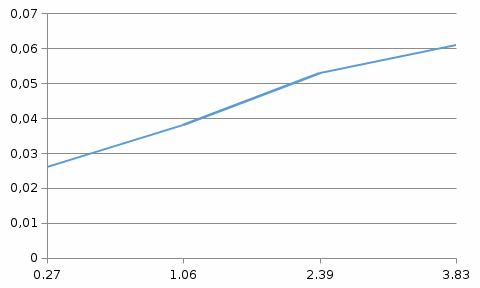 Основной закон динамики вращательного движения: угловое ускорение 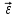 , с которым вращается тело, прямо пропорционально суммарному моменту сил , с которым вращается тело, прямо пропорционально суммарному моменту сил 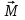 , действующих на тело, и обратно пропорционально моменту инерции телаI относительно оси вращения: , действующих на тело, и обратно пропорционально моменту инерции телаI относительно оси вращения: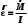 , (1) , (1)Моментом силы 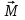 относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора 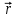 , проведенного из точки О в точку приложения силы, на вектор силы , проведенного из точки О в точку приложения силы, на вектор силы 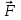 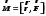 . (2) . (2)Модуль момента силы равен 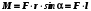 , (3) , (3)где – угол между векторами 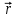 и и 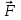 , l – плечо силы. , l – плечо силы.Плечом силы называется кратчайшее расстояние между линией действия силы и точкой О.l = r∙sinα . Как определяется направление углового ускорения и момента сил? Если вектор угловой скорости меняется только по величине, то направление вектора углового ускорения параллельно направлению вектора угловой скорости. Если величина угловой скорости растет, то направление вектора углового ускорения совпадает с направлением вектора угловой скорости. А если величина угловой скорости падает, то направление вектора углового ускорения противоположно направлению вектора угловой скорости. Момент силы является векторной величиной, направление которой определяется по правилу правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление силы, то вытянутый большой палец укажет направление вектора момента силы. Какой физический смысл имеет отрезок, отсекаемый прямой на оси абсцисс на графике ε=f(mgr)? Угловое ускорение прямо пропорционально моменту сил. Какой физический смысл имеет отрезок, отсекаемый прямой на оси абсцисс на графике 1/ε=f(2mοR2)? Угловое ускорение обратно пропорционально моменту инерции. ОТЧЕТ ВЫЧИСЛЕНИЯ: 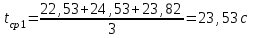 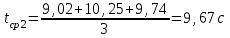 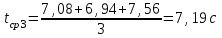 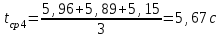 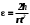 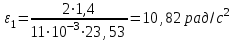 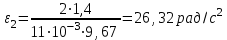 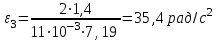 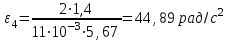 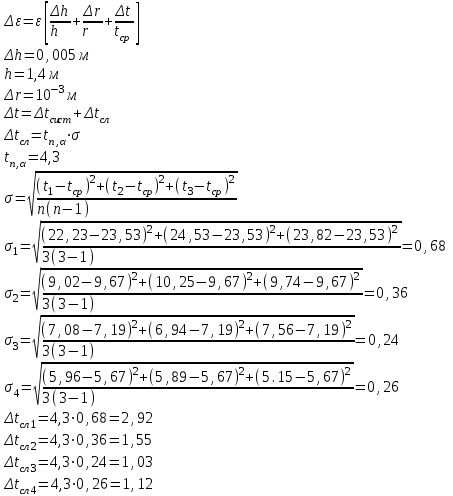 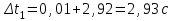 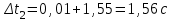 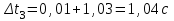 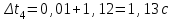 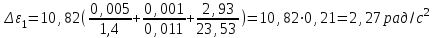 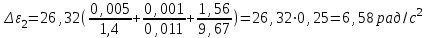 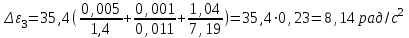 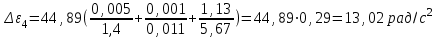 Относительная погрешность: 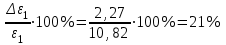 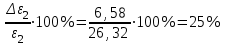 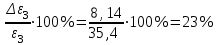 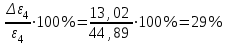 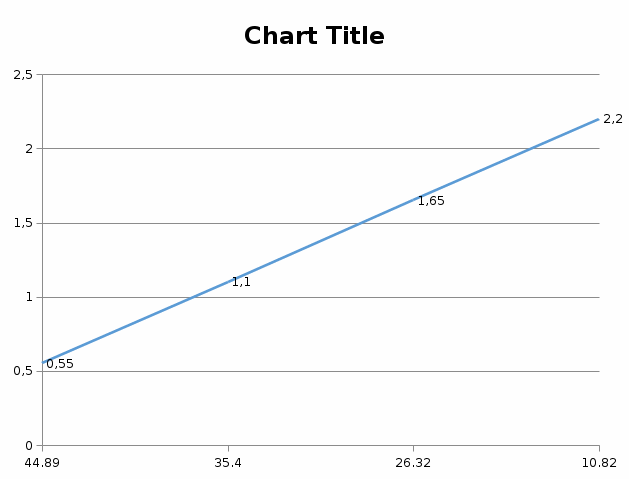 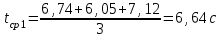 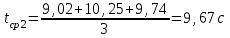 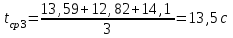 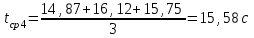 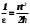 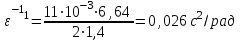 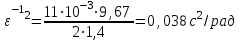 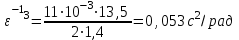 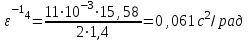 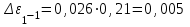 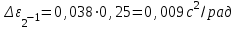 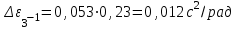 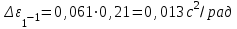 Относительная погрешность: 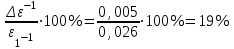 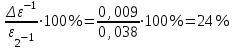 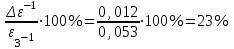 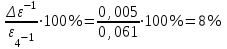
ЛАБОРАТОРНАЯ РАБОТА №13. ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ УДЕЛЬНЫХ ТЕПЛОЕМКОСТЕЙ ГАЗА МЕТОДОМ АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ Цель работы. Ознакомиться с методом адиабатического расширения, определить коэффициент Пуассона для воздуха. Теоретическое введение. Удельной теплоемкостью вещества называется величина, численно равная количеству теплоты, которое необходимо сообщить веществу единичной массы, чтобы увеличить его температуру на один Кельвин: 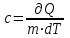 . (1) . (1)Единица удельной теплоемкости в системе СИ – джоуль на килограмм-кельвин: [с] = Дж / (кгК). Молярной теплоемкостью вещества называется величина, численно равная количеству теплоты, которое необходимо сообщить молю вещества, чтобы увеличить его температуру на один Кельвин: 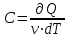 . (2) . (2)Единица молярной теплоемкости в системе СИ – джоуль на моль-кельвин: [С] = Дж / (мольК). Для газов удельная и молярная теплоемкости зависят от условий, при которых проводится нагревание. Между собой теплоемкости связаны соотношением: 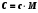 , (3) , (3)где М – молярная масса вещества. Согласно первому началу термодинамикиколичество теплоты 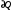 , сообщенное системе, идет на приращение внутренней энергии системы , сообщенное системе, идет на приращение внутренней энергии системы 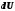 и на работу системы против внешних сил и на работу системы против внешних сил 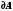 : :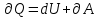 , (4) , (4)Изменение внутренней энергии идеального газа определяется формулой: 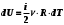 , (5) , (5)где – количество вещества, dT– изменение температуры, R – универсальная газовая постоянная,i – число степеней свободы газа. Для одноатомных молекул (инертные газы) i=3, для двухатомных (простые газы, кроме инертных) – i=5, для многоатомных (сложные газовые соединения) – i=6. Нагреем один моль газа на dT градусов. Если объем газа не изменяется, т.е. V=const, то газ работы не совершает, т.е. 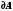 =0. Тогда, согласно уравнению (4) =0. Тогда, согласно уравнению (4) 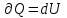 и молярная теплоемкость газа, измеренная при постоянном объеме, определится выражением: и молярная теплоемкость газа, измеренная при постоянном объеме, определится выражением: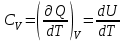 . (6) . (6)Если при нагревании моля газа остается постоянным давление, т.е. P=const, то газ расширяется и совершает работу (рис. 1). Молярная теплоемкость газа, измеренная при постоянном давлении, определяется формулой: 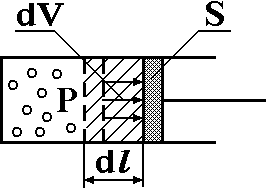 Рис. 1. Расширение газа при нагревании. 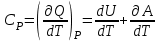 . (7) . (7)Расширившись, газ отодвинет легкий поршень площадью S на расстояние dl(рис. 1). Работа газа 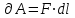 , где F – сила, действующая на поршень. Умножим и разделим правую часть выражения на площадь S, тогда: , где F – сила, действующая на поршень. Умножим и разделим правую часть выражения на площадь S, тогда: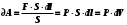 . (8) . (8)Подставив выражения (8) и (6) в (7) получим: 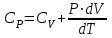 . (9) . (9)Таким образом, чтобы нагреть газ при постоянном давлении, необходимо больше тепла, чем для нагревания такого же количества газа до той же температуры при постоянном объеме, так как в первом случае тепло расходуется не только на повышение внутренней энергии газа, но и на работу газа против внешних сил. Запишем уравнение Клапейрона – Менделеева для моля газа 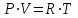 . (10) . (10)Продифференцируем его, считая давление постоянным: 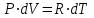 , (11) , (11)отсюда 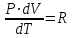 . (12) . (12)Тогда уравнение (9) можно переписать в виде: 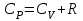 . (13) . (13)Это уравнение называется уравнением Майера. Из соотношения (12) следует физический смысл универсальной газовой постоянной: R числена равна работе изобарного расширения одного моля идеального газа при его нагревании на один Кельвин. Непосредственное определение теплоемкостей довольно затруднительно, особенно CV. При рассмотрении многих задач в расчетные уравнения входит коэффициент Пуассона, который равен отношению теплоемкостей 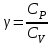 . Измерение коэффициента Пуассона является целью настоящей работы, где он определяется методом Клемана и Дезорма, основанном на адиабатическом расширении газа. . Измерение коэффициента Пуассона является целью настоящей работы, где он определяется методом Клемана и Дезорма, основанном на адиабатическом расширении газа.Адиабатическим процессом называется такой процесс, при котором не происходит теплообмена между исследуемой системой и внешней средой ( 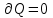 ). Всякое быстрое изменение объема газа приближенно можно рассматривать как процесс адиабатический, и чем быстрее это изменение происходит, тем ближе процесс к адиабатическому. ). Всякое быстрое изменение объема газа приближенно можно рассматривать как процесс адиабатический, и чем быстрее это изменение происходит, тем ближе процесс к адиабатическому. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
