Лаб_Вращ.Обербека-Адиабата-Мостик. Отчет по лабораторной работе по физике факультет Электротехникаэлектроэнергетика
 Скачать 313.92 Kb. Скачать 313.92 Kb.
|
|
Алтайский государственный технический университет им. И.И. Ползунова Кафедра физики ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ ПО ФИЗИКЕ
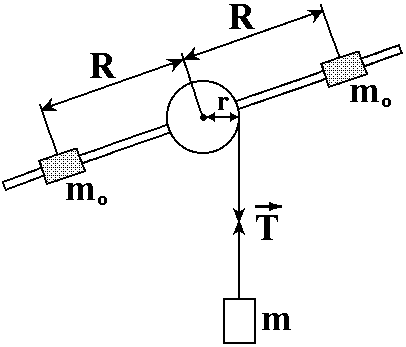
Барнаул - 2020ЛАБОРАТОРНАЯ РАБОТА № 3. ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА Цель работы. Проверить основной закон динамики вращательного движения. Теоретическое введение. Вращательным движением называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Основной закон динамики вращательного движения: угловое ускорение 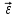 , с которым вращается тело, прямопропорционально суммарному моменту сил , с которым вращается тело, прямопропорционально суммарному моменту сил 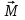 , действующих на тело, и обратнопропорционально моменту инерции телаI относительно оси вращения: , действующих на тело, и обратнопропорционально моменту инерции телаI относительно оси вращения: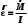 , (1) , (1)Моментом силы 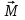 относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора 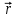 , проведенного из точки О в точку приложения силы, на вектор силы , проведенного из точки О в точку приложения силы, на вектор силы 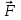 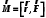 . (2) . (2)Модуль момента силы равен 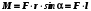 , (3) , (3)где – угол между векторами 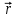 и и 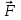 , l – плечо силы. , l – плечо силы.Плечом силы называется кратчайшее расстояние между линией действия силы и точкой О.Из рисунка 1 видно, что l = r∙sinα .
Моментом силы относительно неподвижной оси Z называется скалярная величина MZ, равная проекции на эту ось вектора 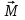 момента силы, определенного относительно произвольной точки О данной оси Z. Значение момента не зависит от выбора положения точки О на оси Z (рис. 2). момента силы, определенного относительно произвольной точки О данной оси Z. Значение момента не зависит от выбора положения точки О на оси Z (рис. 2).Направление вектора момента силы определяется по правилу векторного произведения: если буравчик (винт с правой резьбой) расположить в плоскости, перпендикулярной плоскости расположения векторов, стоящих в векторном произведении и вращать ручку буравчика от первого вектора в векторном произведении ко второму по наименьшему углу, то направление поступательного движения острия буравчика покажет направление вектора, определяемого через данное векторное произведение. Так, в примере на рисунке 1 вектор момента силы 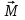 перпендикулярен плоскости, в которой лежат векторы перпендикулярен плоскости, в которой лежат векторы 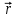 и и 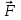 , и направлен в плоскость чертежа “от нас”. Направлению момента силы , и направлен в плоскость чертежа “от нас”. Направлению момента силы 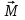 относительно заданной оси Z обычно приписывают направление этой же самой оси (рис. 2). Момент силы, вызывающий вращение тела против часовой стрелки принято считать положительным, по часовой стрелке – отрицательным. относительно заданной оси Z обычно приписывают направление этой же самой оси (рис. 2). Момент силы, вызывающий вращение тела против часовой стрелки принято считать положительным, по часовой стрелке – отрицательным.Угловое ускорение – это векторная физическая величина, которая определяет быстроту изменения угловой скорости: 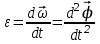 , (4) , (4)где 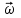 угловая скорость, а угловая скорость, а 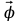 угловое перемещение. угловое перемещение.Единица измерения углового ускорения в системе СИ – радиан на секунду в квадрате (рад/с2). Направление угловой скорости 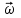 определяется по правилу правого винта: если ручку винта вращать по направлению вращения тела, то направление поступательного движения острия винта покажет направление вектора угловой скорости. Направление углового ускорения определяется по правилу правого винта: если ручку винта вращать по направлению вращения тела, то направление поступательного движения острия винта покажет направление вектора угловой скорости. Направление углового ускорения 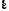 совпадает с направлением вектора угловой скорости совпадает с направлением вектора угловой скорости 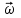 , если движение равноускоренное, и противоположно направлено, если движение равнозамедленное. , если движение равноускоренное, и противоположно направлено, если движение равнозамедленное. В соответствии с основным законом вращательного движения можно сказать, что направление 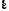 совпадает с направлением результирующего момента силы совпадает с направлением результирующего момента силы 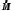 , действующего на тело. , действующего на тело.Моментом инерции материальной точки относительно оси вращения называется произведение массы этой точки на квадрат расстояния от нее до оси вращения: 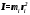 . (5) . (5)Моментом инерции системыматериальных точек (тела) относительно оси вращения называется физическая величина, равная сумме произведения масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси 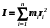 , (6) , (6)где mi масса i-й материальной точки, а ri расстояние от этой точки до оси вращения. Отметим, что момент инерции всегда определяется относительно заданной оси. Момент инерции является мерой инертности тела при вращательном движении. ОПИСАНИЕ УСТАНОВКИ И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Чтобы установить справедливость соотношения (7), необходимо установить справедливость двух зависимостей 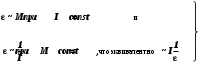 (8) (8)Обозначим через I0 момент инерции маятника без грузов относительно оси вращения, а через Т силу натяжения нити. Тогда результирующий момент инерции маятника окажется равным I = Iο + 2mο R2, (9) где 2mοR2 – момент инерции грузов, находящихся на расстоянии R от оси вращения. Результирующий момент сил равен M = Tr Mтр , (10) где Mтр момент сил трения, возникающий между осью и шкивом, который для каждой установки постоянен. Составим систему уравнений движения маятника и опускающегося груза 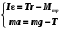 , (11) , (11)где а ускорение опускающегося груза. Умножим второе уравнение системы (11) на радиус шкива r и сложим с первым. При этом следует учесть, что 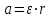 . Тогда . Тогда 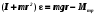 , с учетом формулы (9), получим: , с учетом формулы (9), получим: 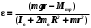 . (12) . (12)Так как при проверке первой зависимости (8) момент инерции системы не изменяется и в соотношении (12) знаменатель остается постоянным, то можно ввести следующие обозначения в выражении (12): I1 = Iο + 2mοR2 + mr2, 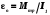 некоторые постоянные. некоторые постоянные.Тогда 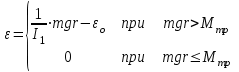 . (13) . (13)Здесь момент силы тяжести груза mgr выступает в качестве аргумента. Установим R равным его среднему значению 10 см. Масса m может быть набрана из трех грузов одного основного 51 г (платформы) и двух дополнительных 51 г и 102 г. Диаметр шкива равен 20 мм, но при наматывании нити конечный диаметр составляет 24 мм. Поэтому можно принять эффективный диаметр шкива равным 22 мм, а эффективный радиус r=11 мм. Ускорение опускающегося груза может быть найдено, как 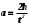 . Тогда с учетом выражения . Тогда с учетом выражения 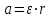 угловое ускорение определится как угловое ускорение определится как 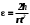 . (14) . (14)Изменение массы груза m производится в соответствии с таблицей 1 исходных данных, в которую так же вносятся результаты измерений и расчетов. Таблица 1
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



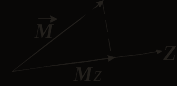
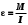 . (7)
. (7)