Алтайский государственный технический университет им. И.И. Ползунова
Кафедра физики
ОТЧЕТ
ПО ЛАБОРАТОРНОЙ РАБОТЕ ПО ФИЗИКЕ
Студент
Группа Факультет
Преподаватель
Барнаул – 2022
Номер варианта и данные к расчету
Лабораторная работа №3
Таблица 1.
-
№
варианта
|
расстояние R, см
|
Высота (расстояние), которое проходит груз
h, м
|
|
время движения груза
|
№
|
t1, c
|
t2, c
|
t3, c
|
4
14
24
|
10
|
1,1
|
1
|
6,38
|
6,41
|
6,45
|
2
|
4,29
|
4,31
|
4,33
|
3
|
3,49
|
3,53
|
3,52
|
4
|
2,93
|
2,92
|
2,95
|
Таблица 2.
-
№
варианта
|
Масса m, г
|
Высота (расстояние), которое проходит груз
h, м
|
|
время движения груза
|
№
|
t1, c
|
t2, c
|
t3, c
|
4
14
24
|
100
|
1,1
|
1
|
3,72
|
3,68
|
3,71
|
2
|
4,05
|
3,99
|
3,97
|
3
|
4,89
|
4,93
|
4,91
|
4
|
5,73
|
5,69
|
5,72
|
ОПИСАНИЕ УСТАНОВКИ И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Д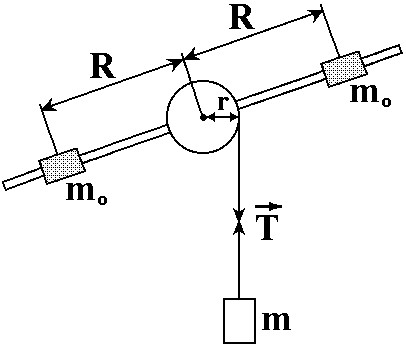 ля проверки основного закона динамики вращательного движения используется установка (рис. 3), называемая маятником Обербека. Она представляет собой шкив с приваренными к нему спицами. На спицах могут перемещаться два груза массой m0 = 53 г каждый, которые
закрепляются специальными винтами
на расстоянии R от оси вращения. На
-
шкиве радиуса r намотана прочная
|
|
нить, к которой прикреплен груз массой m. При свободном опускании груза маятник вращается с постоянным ускорением.
|
Рис. 3. Схема экспериментальной установки машины Обербека.
|
Поскольку ось вращения для маятника Обербека закреплена, то соотношение (1) можно рассматривать в скалярном виде
М
I .
(7)
Чтобы установить справедливость соотношения (7), необходимо установить справедливость двух зависимостей
-
M
1
I
|
при
при
|
I const
M const,
|
и
что эквивалентно
|
1
 I
|
(8
Обозначим через I0 момент инерции маятника без грузов относительно оси вращения, а через Т силу натяжения нити. Тогда результирующий момент инерции маятника окажется равным
I = Iο + 2mο R2, (9)
где 2mοR2 – момент инерции грузов, находящихся на расстоянии R от оси
вращения.
Результирующий момент сил равен
M = Tr Mтр , (10)
где Mтр момент сил трения, возникающий между осью и шкивом, который для
каждой установки постоянен. Составим систему уравнений движения маятника и опускающегося груза
ITr M тр
ma mg T , (11)
где а ускорение опускающегося груза.
Умножим второе уравнение системы (11) на радиус шкива r и сложим с первым.
При этом следует учесть, что a r . Тогда (I mr 2)mgr M тр , с учетом формулы (9), получим:
(mgr Mтр)
(Iо o 2 mr2) . (12) 2m R
Так как при проверке первой зависимости (8) момент инерции системы не изменяется и в соотношении (12) знаменатель остается постоянным, то можно ввести следующие обозначения в выражении (12):
I1 = Iο + 2mοR2 + mr2, o Mтр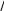 I1 некоторые постоянные.
1
 mgr o при mgr Mтр
I1
0 при mgr Mтр .
Тогда
(13)
Здесь момент силы тяжести груза mgr выступает в качестве аргумента. Установим R равным его среднему значению 10 см. Масса m может быть набрана из трех грузов одного основного 50 г (платформы) и двух дополнительных 50 г и 100 г. Диаметр шкива равен 20 мм, но при наматывании нити конечный диаметр составляет 24 мм. Поэтому можно принять эффективный диаметр шкива равным 22 мм, а эффективный радиус r=11 мм. Ускорение опускающегося груза может быть 2h
a t 2 . Тогда с учетом выражения a r угловое ускорение найдено, как
|
Скачать 0.61 Mb.