КМЭП. КМ ПЗ 14 МежотраслБаланс. Отчет по национальной экономике по итоговым данным за фиксированный период времени, например, за прошедший год, представленный в таблице 1

Название	Отчет по национальной экономике по итоговым данным за фиксированный период времени, например, за прошедший год, представленный в таблице 1
Дата	12.12.2022
Размер	398.5 Kb.
Формат файла
Имя файла	КМ ПЗ 14 МежотраслБаланс.doc
Тип	Отчет #841586
страница	2 из 3

1 2 3

>restart:Digits:=5

>with(‘linalg’): # вызов пакета линейной алгебры

Модель межотраслевого баланса экономики США по данным 1958 г. (млн. дол.) задана следующей таблицей

> Balance:=array(1..12,1..12,[

[Sek, 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , Sum , Prod , ValVup],

[1, 8565, 8069, 8843, 3045, 1124, 276, 230, 3464, 33616, 3992, 37608],

[2, 1505, 6996, 6895, 3530, 3383, 365, 219, 2946, 25839, 19261, 45100],

[3, 98, 39, 5, 429, 5694, 7, 376, 327, 6975, 39347, 46322],

[4, 999, 1048, 120, 9143, 4460, 228, 210, 2226, 18434, 22625, 41059],

[5, 4373, 4488, 8325, 2729, 29671, 1733, 5757, 14756, 71832, 137572, 209404],

[6, 2150, 36, 640, 1234, 165, 821, 90, 6717, 11853, -654, 11199],

[7, 506, 7, 180, 0, 2352, 0, 18091, 26529, 47665, 8327, 55992],

[8, 5315, 1895, 2993, 1071, 13941, 434, 6096, 46338, 78083, 82997, 161080],

[Sum, 23511, 22578, 28001, 21181, 60790, 3864, 31069, 103303, 294297, 313467, 607764],

[Doh, 14097, 22522, 18321, 19878, 148614, 7335, 24923, 57777, 313467, xxxxxx , xxxxxx],

[Zat, 37608, 45100, 46322, 41059, 209404, 11199, 55992, 161080, 607764, xxxxxx, 607764]]);

Sek 1 2 3 4 5 6 7 8 Sum Prod ValVup

1 8565 8069 8843 3045 1124 276 230 3464 33616 3992 37608

2 1505 6996 6895 3530 3383 365 219 2946 25839 19261 45100

3 98 39 5 429 5694 7 376 327 6975 39347 46322

4 999 1048 120 9143 4460 228 210 2226 18434 22625 41059

Balance= 5 4373 4488 8325 2729 29671 1733 5757 14756 71832 137572 209404

6 2150 36 640 1234 165 821 90 6717 11853 -654 11199

7 506 7 180 0 2352 0 18091 26529 47665 8327 55992

8 5315 1895 2993 1071 13941 434 6096 46338 78083 82997 161080

Sum 23511 22578 28001 21181 60790 3864 31069 103303 294297 313474 607764

Doh 14097 22522 18321 19878 148614 7335 24923 57777 313467 xxxxxx xxxxxx

Zat 3760 45100 46322 41059 209404 11199 55992 161080 607764 xxxxxx 607764

Где:

Sek – отрасли ( секторы), Sum – промежуточные затраты или промежуточный спрос;

Doh – добавленная стоимость, Zat затраты отрасли, Prod – конечный спрос, ValVup – выпуск продукции.

1 -отрасль материалов, 2 - металлообрабатывающие отрасли, 3 - строительство ,

4 - отрасль, которая объединяет транспортное оборудование, электрику и газ,

5 - услуги и транспорт, 6 - горнодобывающая промышленность,

7 - сельское хозяйство и сопредельные отрасли, 8 - все другие отрасли .

В отличие от таблицы 1 матрица Balance (начальная) имеет дополнительный столбец Sum и дополнительную строку Sum – суммы коэффициентов α по столбцам и по срокам.

Спланируем выпуск продукции в отраслях промышленности в млн. долларов США, чтобы удовлетворить потребление по каждой отрасли, заданного таблицей 3.

Таблица 3

Номер отрасли	Объем продукции отрасли, которая направляется на потребление (млн. дол.)
1	6000
2	40000
3	39000
4	22000
5	300000
6	500
7	8000
8	90000

Формируем матрицу коэффициентов прямых затрат, которая соответствует этой таблице:

Образовываем матрицу Qinner размером 8х8 из элементов α путем их изъятия из матрицы Balance с помощью функции submatrix >Qinner:=submatrix(Balance,2..9,2..9);

Образовываем матрицу прямых затрат путем деления элементов столбцов матрицы Rash на общий объем затрат по каждой отрасли, которые выбираются из 12-той сроки матрицы
Balance.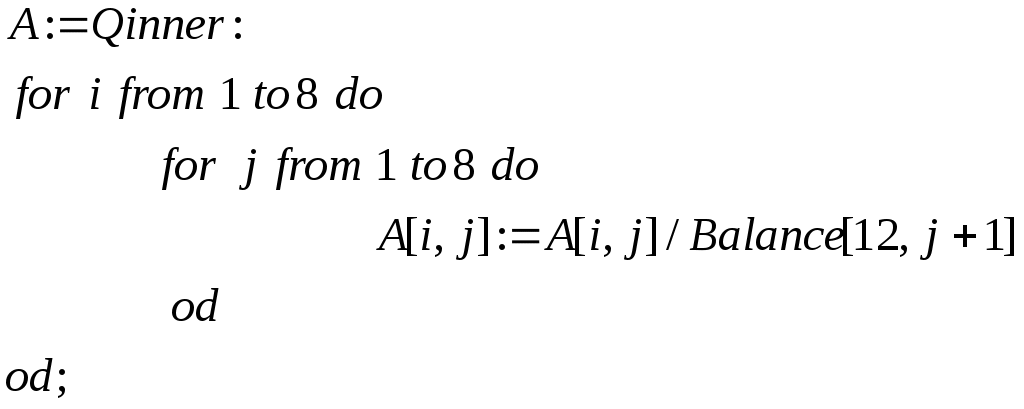

>convert(eval(A),float,7):

> ;
.2277441 .1789135 .1909069 .07416338 .005367615 .02462527 .004107730 .02150484

.04001808 .1551220 .1488526 .08597594 .01615537 .03256602 .003911273 .01828905

.002605829 .00086474 .0001079424 .01044863 .02719146 .00062455 .006715245 .00203004

.02656350 .02323725 .002590618 .2226850 .02129854 .02034261 .003750536 .01381922

.1162785 .09951220 .1797241 .06646695 .1416926 .1546217 .1028183 .09160666

.05716869 .00079822 .01381663 .03005504 .000787950 .07325125 .001607372 .04169978

.01345458 .00015521 .003885926 0 .01123188 0 .3230997 .1646946

.

1413263 .04201774 .06461432 .02608505 .06657466 .03872234 .1088727 .2876707

Проверяем условия Хаукинса-Саймона. Для этого сформируем единичную диагональную матрицу:

>II:=band([1],8);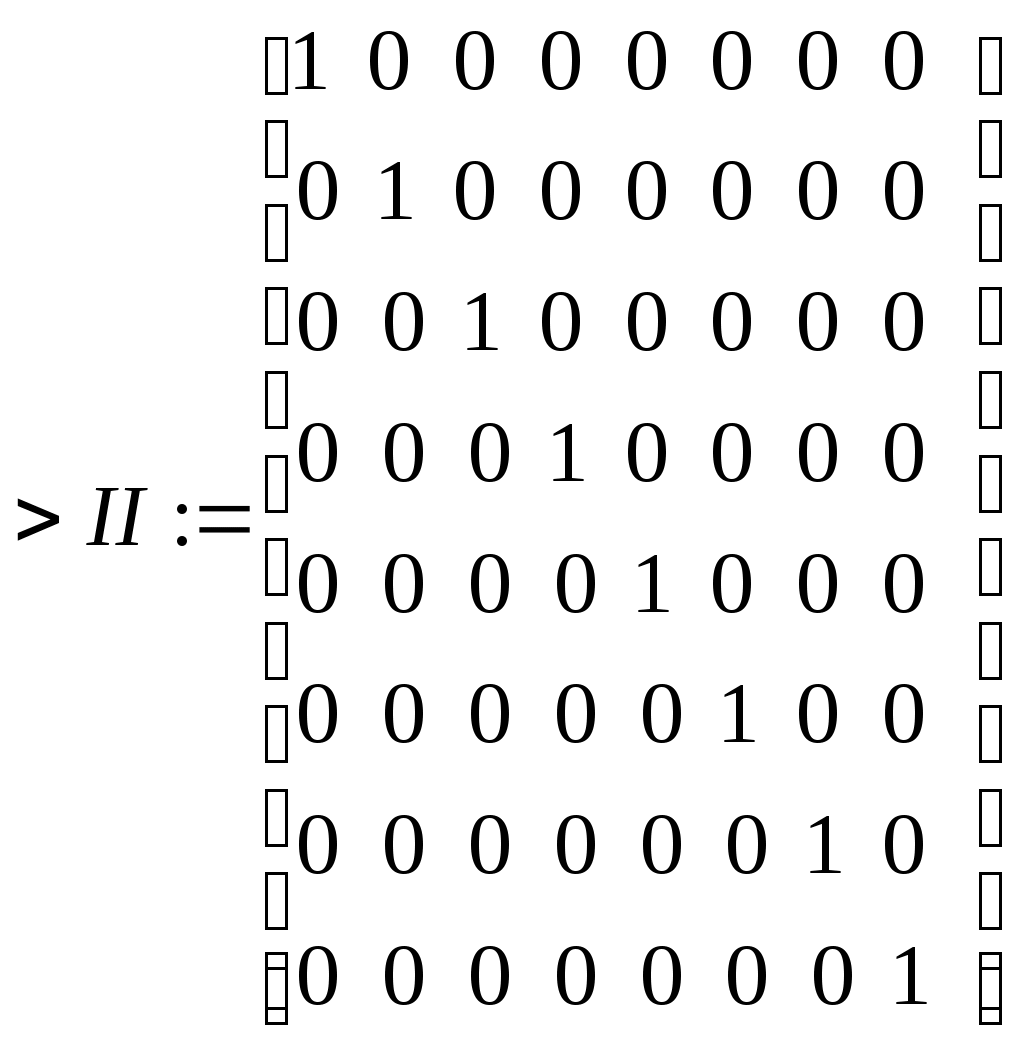

. det(Dob); det(submatrix(Dob,1..7,1..7); больше нуля и т.д.

С помощью матричных операций вычисляем обратную матрицу Леонтьева

>KPZ:=evalm((II-A)^(-1));

Просчет контрольного примера.

Формируем матрицу конечного спроса по 11-му столбцу матрицы Balance, которая описывает экономику США.

>D1:=matrix(8,1,[3992,19261,39347,22625,137572,-654,8327,82997]: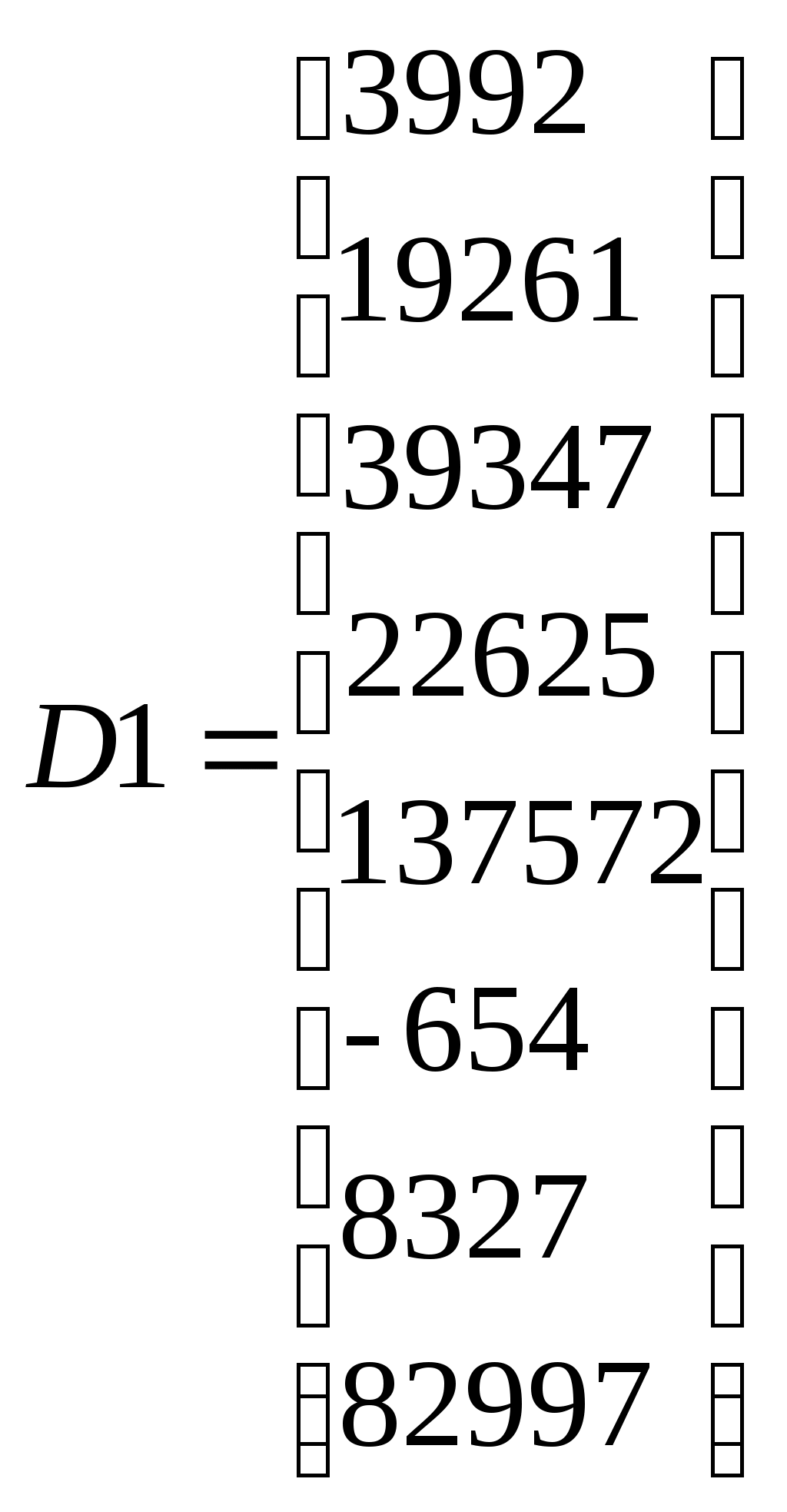

Так как символ D зарезервирован за обозначением дифференциального оператора, то для обозначения вектора-столбца конечного спроса (demand) выбран идентификатор D1.

Вычисляем объемы выпуска по каждой отрасли

>Х1:= multiply(KPZ,D1);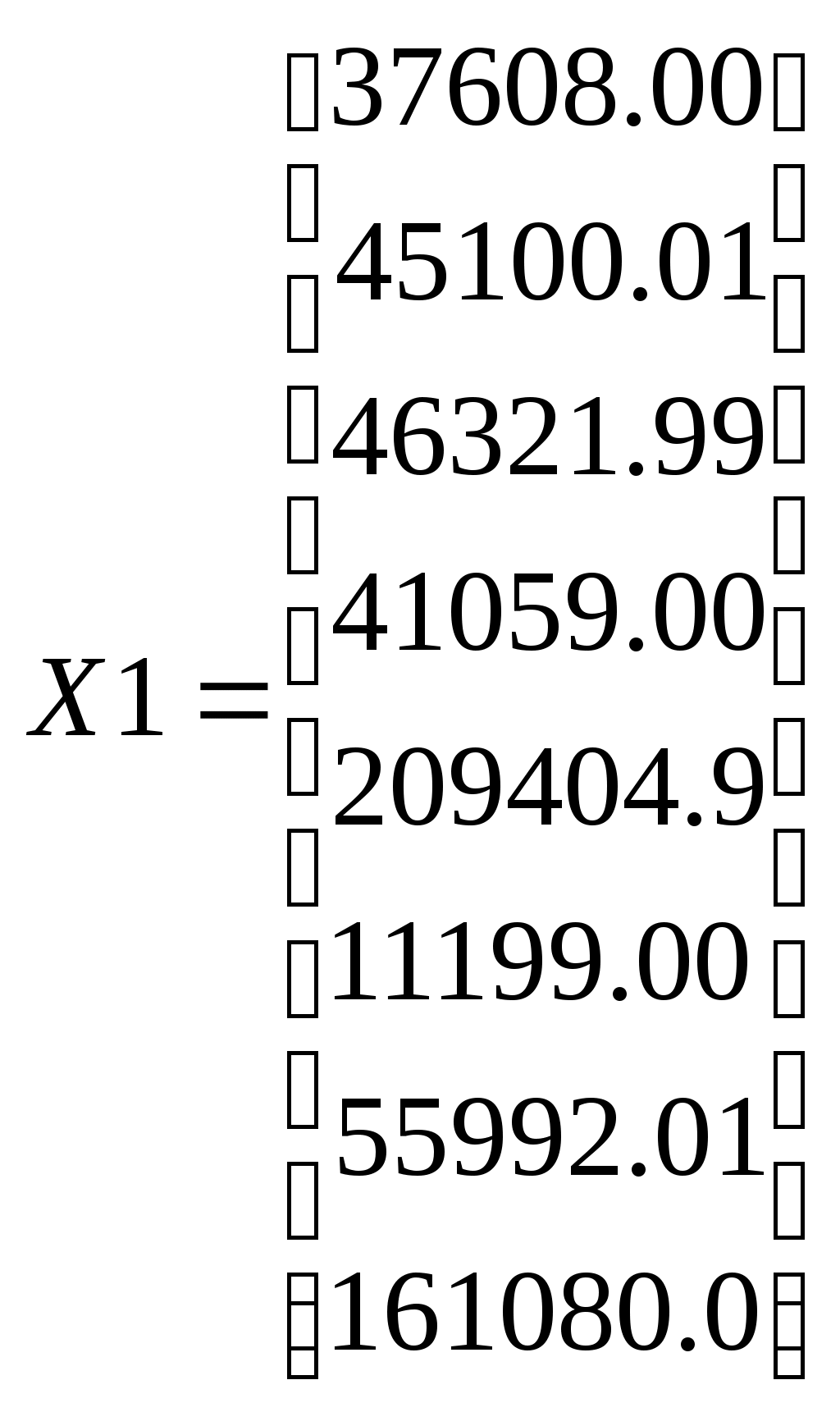

Эти значения до долей процента совпадают со значениями валового выпуска по каждой отрасли, поэтому заключаем, что модель работает с довольно большой точностью.

Р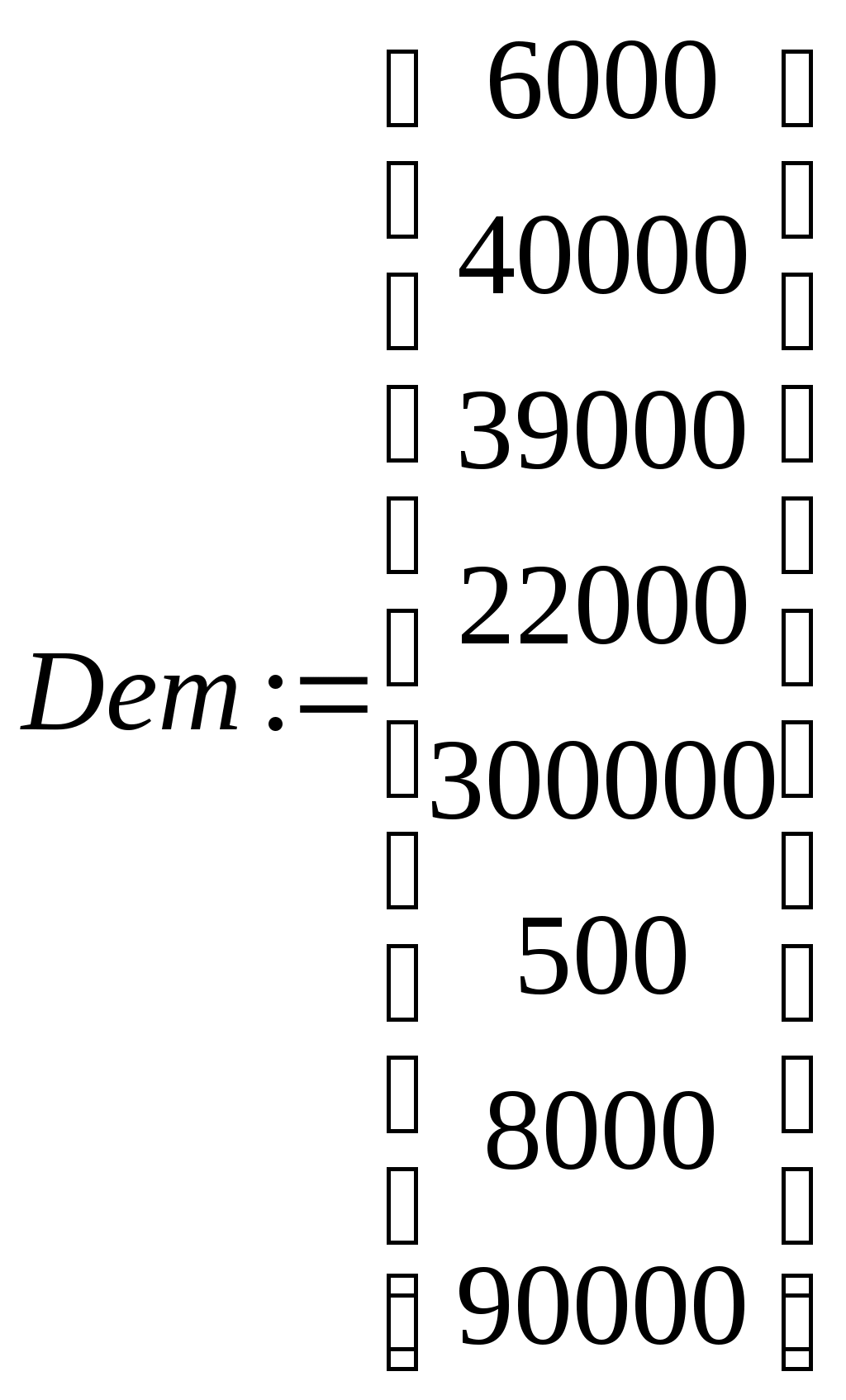

ешим поставленную задачу. Формируем матрицу конечного спроса.

> Dem:=matrix(8,1,[6000,40000,39000,22000,300000,500,8000,90000]);

Находим потребный выпуск продукции промышленности в млн. долларов США, чтобы удовлетворить потребление по каждой отрасли, заданного таблицей 6.3.

X2:=multiply(KPZ,Dem);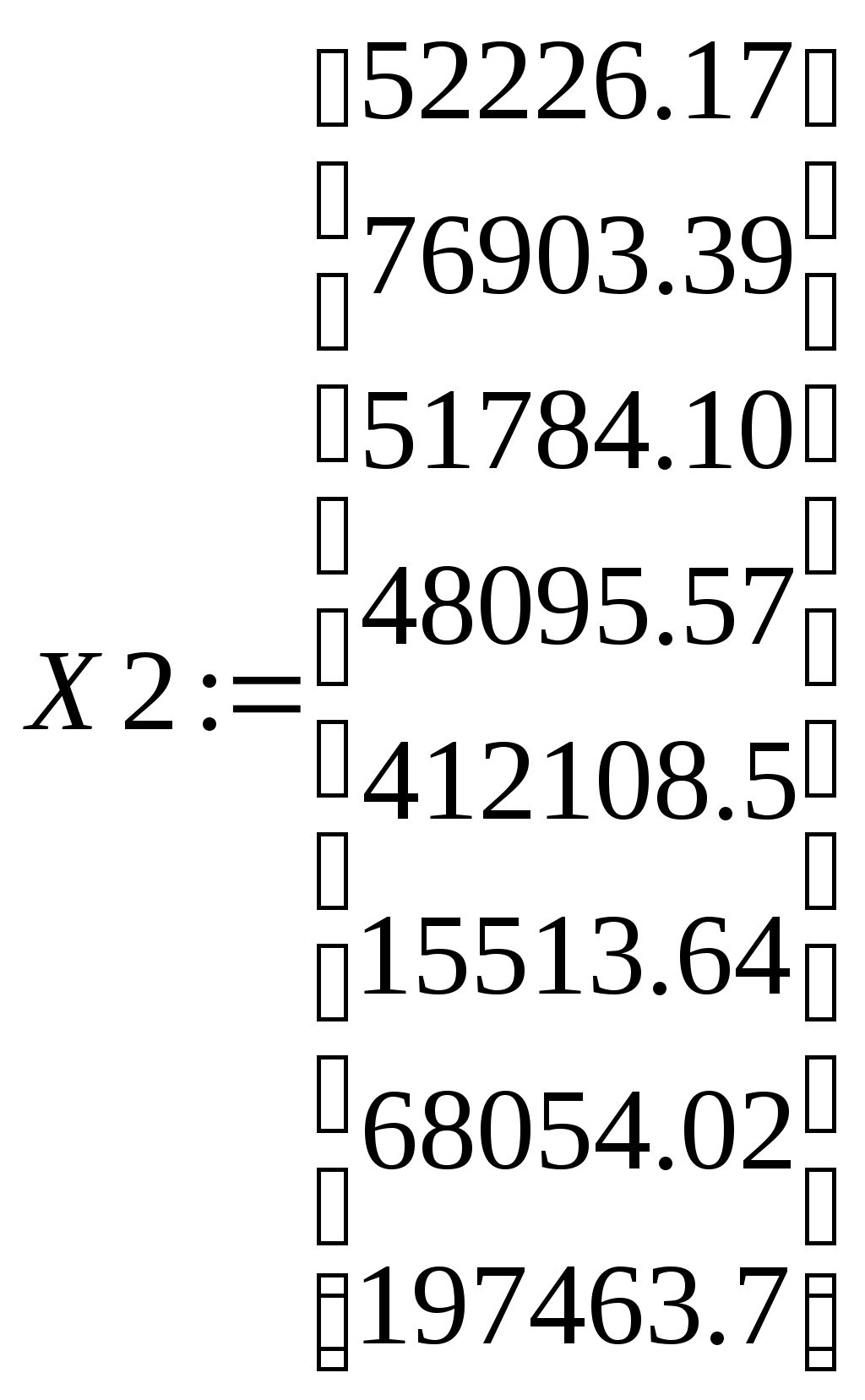

Аналогично можно планировать производство и при других показателях.
2. Задания к практическому занятию

Модель экономики задана укрупненной таблицей межотраслевого баланса (см. варианты заданий). А - сельское хозяйство, В — промышленность, С — транспорт, D — сектор конечного спроса (домашние хозяйства), D2 — измененный конечный спрос). :

Найдите объем выпуска каждой отрасли при заданном конечном спросе D.
Рассчитайте объем добавленной стоимости в каждой отрасли (если она отрицательная, то объясните ее экономический смысл).
Сформируйте матрицу коэффициентов прямых затрат.
С помощью условий Хаукинса-Саймона определите продуктивность модели.
Найдите матрицу полных затрат (обратную матрицу Леонтьева) .
Проверьте теорию баланса (рассчитайте потребный объем выпуска по модели Леонтьева при заданном спросе D и сравните его с рассчитанным по п. 1).
Найдите объем выпуска каждой отрасли при новом конечном спросе D2;
Измените конечный спрос на продукцию отрасли сельское хозяйство на 20% и определите, на сколько процентов изменится объем выпуска каждой отрасли;

3. Варианты задания

№		A	B	C	D	D2	№		A	B	C	D	D2
1	А	10	16	50	20	96	16	А	130	88	650	140	100
	В	3	5	40	23	81		В	43	75	520	63	701
	С	2	26	ЗО	32	90		С	32	98	390	62	582
2	А	20	22	100	З0	172	17	А	140	94	700	150	108
	В	6	20	80	26	132		В	46	80	560	66	752
	С	5	32	60	35	132		С	35	104	420	65	624
3	А	ЗО	28	150	40	248	18	А	10	16	50	20	96
	В	10	25	120	ЗО	185		В	3	15	40	23	81
	С	7	38	90	37	172		С	2	26	ЗО	32	90
4	А	40	34	200	50	324	19	А	20	16	50	20	106
	В	13	З0	160	33	236		В	3	15	40	23	81
	С	10	44	120	40	214		С	22	26	ЗО	32	110
5	А	50	40	250	60	400	20	А	70	52	350	80	552
	В	16	35	200	36	287		В	23	45	280	43	391
	С	12	50	150	42	254		С	17	62	210	47	336
6	A	60	46	300	70	476	21	А	90	64	450	100	704
	B	20	40	240	40	340		В	ЗО	55	360	50	495
	С	15	56	180	45	296		С	22	74	270	52	418
7	А	70	52	350	80	552	22	А	100	70	500	11	780
	В	23	45	280	43	391		В	33	60	400	53	546
	С	17	62	210	47	336		С	25	80	300	55	460
8	A	80	58	400	90	628	23	A	90	64	450	100	704
	в	26	50	320	46	442		в	ЗО	55	360	50	495
	С	20	68	240	50	378		С	22	74	270	52	418
9	А	90	64	450	100	704	24	А	60	46	300	70	476
	В	10	55	360	50	495		В	20	40	240	40	340
	С	22	74	270	52	418		C	15	56	180	45	296
10	А	60	46	300	70	476	25	A	100	70	500	110	780
	В	20	40	240	40	340		B	33	60	400	53	546
	C	15	56	180	45	296		С	25	80	300	55	460
II	А	100	70	500	110	780	26	А	60	46	300	70	476
	В	33	60	400	53	546		В	20	40	240	40	340
	С	25	80	300	55	460		С	15	56	180	45	296
12	А	70	52	350	80	552	27	А	70	52	350	80	552
	В	23	45	280	43	391		В	23	45	280	43	391
	С	17	62	210	47	336		С	17	62	210	47	336
13	А	90	64	450	100	704	28	А	80	58	400	90	628
	В	ЗО	55	360	50	495		В	26	50	320	46	442
	С	22	74	270	52	418		С	20	68	240	50	378
14	А	100	70	500	11	780	29	А	40	34	200	50	324
	В	33	60	400	53	546		В	13	30	160	33	236
	C	25	80	300	55	460		С	10	44	120	40	214
15	А	90	64	450	100	704	30	А	50	40	250	60	400
	В	36	65	440	56	597		В	16	35	200	36	287
	С	27	86	330	57	500		С	12	50	150	42	254

1 2 3