КМЭП. КМ ПЗ 14 МежотраслБаланс. Отчет по национальной экономике по итоговым данным за фиксированный период времени, например, за прошедший год, представленный в таблице 1
 Скачать 398.5 Kb.
|
|
25.04.10 г. Компьютерное моделированиеПрактическое занятиеКомпьютерная модель межотраслевого баланса1. Теоретическое введениеЛюбое национальное хозяйство развивается в сложной системе межотраслевых взаимосвязей, понять которые во всей их совокупности путем простого суммирования невозможно. Например, спрос на автомобили оказывает влияние не только на автомобильную промышленность, но и косвенным путем на металлургию и области, которые вырабатывают шины, бортовую электронику, а через них на производство микросхем. Изменения в одной области неизбежно сказывается во всем народном хозяйстве. Для анализа межотраслевых связей выдающийся экономист Леонтьев В.В. разработал специальный метод балансового анализа – “анализ затрата-выпуск” (Input-output analysis или I/O analysis), который позволяет исследовать процессы, связанные с межотраслевыми взаимодействиями. Цель балансового анализа — определить, сколько продукции должна выработать каждая отрасль для того, чтобы удовлетворить все потребности национального хозяйства системы в его продукции. Пусть весь производственный сектор национальной экономике условно разделен на n “чистых отраслей ” (секторов). Словосочетание “чистая область” означает, что продукция каждой области является однородной и что каждая отрасль выпускает продукцию только одного вида и разные отрасли вырабатывают разную продукцию. В процессе производства своего вида продукции каждая отрасль потребляет продукцию других отраслей. Пусть в какой-либо момент времени Т0 составлен балансовый отчет по национальной экономике по итоговым данным за фиксированный период времени, например, за прошедший год, представленный в таблице 1. Таблица .1
Строки приведенной таблицы показывают распределение выпуска (output) каждого вида продукции. Величина ij показывает объем продукции отрасли i, которую закупили у нее отрасли j ( i, j = 1,2,…)в качестве промежуточных продуктов. Конечный спрос di показывает объем продукции i-й отрасли, который был потреблен на инвестиции, экспорт, для создания запасов. Число qi равняется общему объему продукции (валовому выпуску) i-й отрасли за отчетный период. Каждая строка характеризуется следующим балансом: выпуск данного вида продукции = промежуточный спрос + конечный спрос, который математически может быть записан как  (1)Столбцы таблицы показывают структуру затрат (input), или структуру используемых ресурсов, необходимых для каждой отрасли. Для столбцов устанавливается следующий баланс: затраты отрасли = промежуточные затраты + добавленная стоимость что в математической записи выглядит как  (2)Промежуточные затраты  являются исходными материалами, закупленными i – й отраслью у отраслей (секторов) j=1,2,...,n. Добавленная стоимость – gявляется факторными затратами отрасли, то есть вновь приобретенной стоимостью, которая распадается на заработную плату, предпринимательскую прибыль, амортизационные отчисления. Для национальной экономики исходя из закона сохранения должны выполняться отношения: Выпуск отрасли = затраты отрасли, Общая сумма конечного спроса = общая сумма добавленной стоимости. Математически это записывается следующим образом:  (3)  (4)Уравнения (3) и (4) называются балансовыми уравнениями. Единицами измерения всех указанных величин могут быть или натуральными (тонны, штуки) или стоимостными, в зависимости от чего различают натуральный и стоимостный баланс. В будущем будим иметь в виду стоимостный баланс. Таблица 1 также называется таблицей межотраслевого баланса и она позволяет изучать структуру потоков ресурсов в национальной экономике. Но более информативными являются относительные величины. Если все элементы αijтаблицы 1 разделить на величину qj (объем продукции j – й отрасли), а числа di на qi , то числа aij =αij /qj , i,j = 1,2,…,n, можнопонимать как объем продукции i - й отрасли, необходимой для производства одной единицы продукции отрасли с номером j; числа ci = di / qi , i = 1,2,…,n, как долю продукции i –й отрасли, которая пошла на непроизводственное потребление. Числа aij ,i = 1,2,…,n, носят название коэффициентов прямых, непосредственных затрат j – й отрасли и в некотором смысле полностью характеризуют технологию j – й отрасли в отчетном периоде: выпуск единицы продукции возможен при структуре затрат, характеризуемыми величинами aij. Исходя из экономического смысла, считаем коэффициенты aij положительными. Матрица А=[ aij ], составленная из коэффициентов прямых затрат aij , несет много информации о структуре межотраслевых связей и существующей технологии общественного производства, которые сложились в народном хозяйстве. Сравнивая такие матрицы, составленные в разные моменты времени, можно прогнозировать направления изменения и развития технологии. Например, некоторые коэффициенты затрат труда при семидесяти шести отраслевой схеме классификации отраслей народного хозяйства США имеют вид Таблица 2
Из таблицы 2 видно, что вследствие внедрения прогрессивной технологии резко уменьшились затраты на производство автомобилей и нефтепереработку, но в сфере ремонта автомобилей, где преобладает ручной труд, относительные затраты возросли. Матрицу А можно использовать для текущего и долгосрочного планирования. Сделаем следующие предположения: Существующая технология производства неизменна в течение некоторого промежутка времени [T0, T], где Т>T0 . В зависимости от поставленной задачи промежуток [T0, T] может равняться одному календарному периоду (год) или нескольким. Технология производства линейная, то есть будем считать, что для выпуска продукции i-й отрасли объемом xi необходимо и достаточно сделать затраты в объемах xiaij , j=1,2,…,n, продукции каждой отрасли. Все это вместе приводит к тому, что мы будем рассматривать идеализацию реальных процессов - модель. Мы не можем производить какой угодно объем продукции, так как не хватит прежде всего производственных мощностей. Пусть i-яотрасль должна вырабатывать объем xi, i=1,2,…,n, валового выпуска своей продукции. Обозначим через X =[  , ,…., ]T матрицу-столбец валового выпуска всех секторов. Воспользовавшись предположением о линейности, рассчитаем затраты отрасли iна выпуск продукции в других отраслях. Это будет  . (5)Из уравнения баланса вытекает, что выражение (5) равняется xi минус конечный спрос, то есть  где  конечный спрос на продукцию i-й отрасли.В матричном виде AX = X - D, или ( I – A ) X = D, (6) где D - вектор конечного спроса национальной экономики, I – единичная матрица. Уравнение (6) вместе с интерпретацией матрицы A и векторов X, D называется моделью Леонтьева. При планировании ставится задача: найти вектор X валового выпуска, чтобы удовлетворить вектор конечного спроса D при существующей структуре экономики, которая задается матрицей A. Если задан вектор конечного спроса D и существует положительный вектор производства X, который удовлетворяет уравнению (6), то модель Леонтьева называется продуктивной. Для установления продуктивности модели Леонтьева необходимы выполнения условия Хаукинса-Саймона: 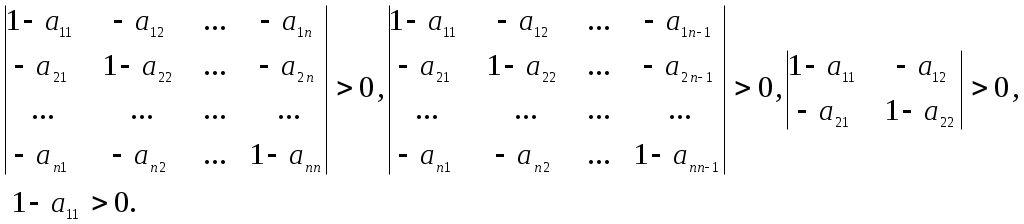 (7) О (8) пределители выделяются из матрицы (I – A ). Решение уравнения (6) имеет вид: X = (I – A )-1D = KPZ∙D, где матрица KPZ = (I-A)-1 называется матрицей полных затрат или обратной матрицей Леонтьева. KPZявляется ни чем иным, как матрицей коэффициентов полных затрат. Экономическое содержание ее элементов KPZijзаключается в следующему: коэффициент KPZij показывает общую потребность в валовом выпуске продукции отрасли iдля производства единицы конечной продукции отрасли j. Например, для выпуска автомобилей нужна продукция металлургической отрасли, это будет первичный спрос; также нужны подшипники, для выпуска которых также нужна продукция металлургической отрасли – это образует вторичный спрос со стороны отрасли автомобилестроения на продукцию металлургической отрасли и так далее. В сумме это сформирует полную потребность в продукции металлургической отрасли со стороны автомобилестроения. Рассмотрим процедуру планирования с использованием модели Леонтьева на примере данных экономики США за 1958 год в системе Maple. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||