Математическое моделирование систем и процессов лабараторные. Отчет по практическим занятиям дисциплины Математическое моделирование систем и процессов
 Скачать 1.33 Mb. Скачать 1.33 Mb.
|
|
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯСамарский государственный университет путей сообщения(СамГУПС) Кафедра «Вагоны» ОТЧЕТ по практическим занятиям дисциплины «Математическое моделирование систем и процессов» Вариант № 01 Выполнил: Акимова Н.А. Группа: ПСЖД-03 Проверил: Балалаев А.Н. Самара 2022 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №1 Составление требований к модели системы «Вагон – среда» Цель занятия: ознакомиться с методами математического моделирования подвижного состава с использованием системного подхода на примере моделирования системы «вагон-среда». Программа определения оптимального расстояния между ПТО в системе Mathcad при начальных параметрах приведена на рис 1.  Рис. 1. Листинг программы определения оптимального расстояния между ПТО в системе Mathcad при начальных параметрах Программа определения оптимального расстояния между ПТО в системе Mathcad при изменении параметра b1 приведена на рис. 2.  Рис. 2. Листинг программы определения оптимального расстояния между ПТО в системе Mathcad при увеличении параметра b1 на 1% (число, равное номеру варианта) Программа определения оптимального расстояния между ПТО в системе Mathcad при изменении параметра b2 приведена на рис. 3.  Рис. 3. Листинг программы определения оптимального расстояния между ПТО в системе Mathcad при увеличении параметра b2 на 1% (число, равное номеру варианта) Программа определения оптимального расстояния между ПТО в системе Mathcad при изменении параметра b3 приведена на рис. 4.  Рис. 4. Листинг программы определения оптимального расстояния между ПТО в системе Mathcad при увеличении параметра b3 на 1% (число, равное номеру варианта) Программа определения оптимального расстояния между ПТО в системе Mathcad при изменении параметра а2 приведена на рис. 5.  Рис. 5. Листинг программы определения оптимального расстояния между ПТО в системе Mathcad при увеличении параметра а2 на 1% (число, равное номеру варианта) Программа определения оптимального расстояния между ПТО в системе Mathcad при изменении параметра а4 приведена на рис. 6.  Рис. 6. Листинг программы определения оптимального расстояния между ПТО в системе Mathcad при увеличении параметра а4 на 1% (число, равное номеру варианта) Выводы: анализ рис. 2 – 6 показал, что при увеличении b1 на 1% безразмерный параметр С увеличивается на 3,2%, при увеличении b2 на 1% безразмерный параметр С увеличивается на 0,0004471%, при увеличении b3 на 1% безразмерный параметр С уменьшается на 102,2%, при увеличении а2 на 1% безразмерный параметр С увеличивается незначительно (изменением можно пренебречь), при увеличении а4 на 1% безразмерный параметр С уменьшается на 3,3% ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №2 Составление модели надежности вагона в эксплуатации с целью определения оптимальной длины гарантийного участка Цель занятия: ознакомиться с методами математического моделирования параметров надежности подвижного состава на примере составления модели надежности вагона в эксплуатации. Исходные данные взяты из таблицы 2 методических указаний № 4954 и внесены в таблицу 1. Таблица 1 – Исходные данные к расчетам по практическому занятию №2
На рисунке 1 показан листинг программы аппроксимации зависимости между вероятностью безотказной работы вагона и длиной гарантийных участков полиномом первой степени:  Рис. 1. Листинг программы аппроксимации зависимости между вероятностью безотказной работы вагона и длиной гарантийных участков полиномом первой степени На рис. 2 показан листинг программы аппроксимации зависимости между вероятностью безотказной работы вагона и длиной гарантийных участков полиномом второй степени:  Рис. 2. Листинг программы аппроксимации зависимости между вероятностью безотказной работы вагона и длиной гарантийных участков полиномом второй степени На рис. 3 показан листинг программы аппроксимации зависимости между вероятностью безотказной работы вагона и длиной гарантийных участков полиномом третьей степени:  Рис. 3. Листинг программы аппроксимации зависимости между вероятностью безотказной работы вагона и длиной гарантийных участков полиномом третьей степени Выводы: среднеквадратичная погрешность аппроксимации уменьшается с увеличением порядка аппроксимации, величина вероятности безотказной работы при аппроксимирующем полиноме 1-го порядка равна P(870) = 0,998531 при длине гарантийного плеча 870 км, при полиноме 2-го порядка 0,998804, при полиноме 3-го порядка 0.9988. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3 Составление модели деповского ремонта вагона с целью определения предельной годовой программы ремонта Цель занятия: овладеть навыками решения уравнений методом деления отрезка пополам на примере определения предельной годовой программы ремонтного депо. Исходные данные из табл. 3 методических указаний № 4954. Таблица 1 – Исходные данные к расчетам по практическому занятию №3
Результаты расчетов по определению предельной годовой программы ремонтного депо в среде Just BASIC v2.0 представлены на рис. 1. 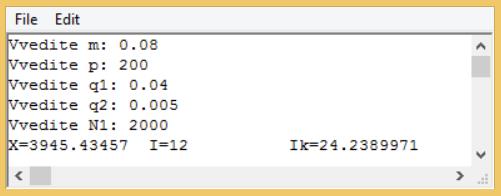 Рис. 1. Результаты расчетов по определению предельной годовой программы ремонтного депо в среде Just BASIC v2.0 Результаты расчетов по определению предельной годовой программы ремонтного депо в среде Mathcad представлены на рис. 2. 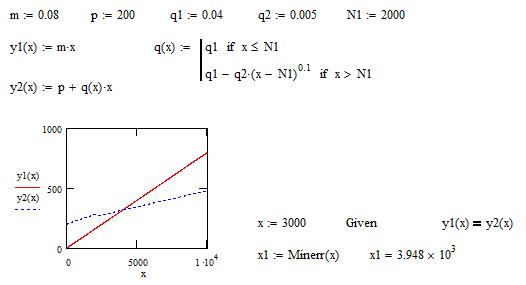 Рис. 2. Результаты расчетов в среде Mathcad Вывод: предельная годовая программа ремонтного депо, рассчитанная в Just BASIC v2.0, равна 3945.4, а в среде Mathcad – 3948. Относительная разность составила (3945.4 – 3948) / 3948 = 0.000659 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №4 Составление сетевого графика технологического процесса деповского ремонта полувагона Цель занятия: ознакомиться с сетевым моделированием процессов ремонта подвижного состава на примере исследования сетевой модели деповского ремонта полувагона. Исходные данные из табл. 6 методических указаний № 4954. Таблица 1 – Исходные данные к расчетам по практическому занятию №4
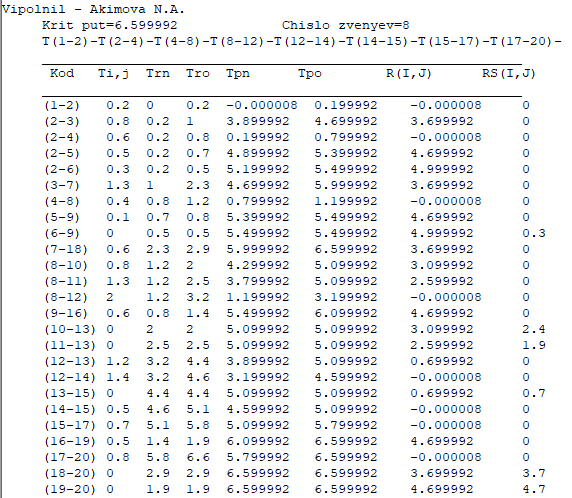 Результаты расчетов критического пути и резервов времени технологического процесса ремонта полувагона показаны на рис. 1. Рис. 1. Результаты расчета критического пути и резервов времени Выводы: Максимальный свободный резерв времени выпадает на фиктивную работу Т(19-20), он начинается в 1.9 часа от начала работ и заканчивается в 6.6 часа, продолжается 4.7 часа. Им располагает исполнитель предыдущей работы Т(16-19). После выполнения работы Т(16-19) этого исполнителя можно переводить на работы критического пути, которые являются «ручными» и время исполнения которых находится в диапазоне резерва времени: - Т(12-14) начинается в 3.2 часа, заканчивается в 4.6 часа; - Т(14-15) начинается в 4.6 часа, заканчивается в 5.1 часов; - Т(17-20) начинается в 5.8 часа, заканчивается в 6.6 часа. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №5 Построение оптимального плана эксперимента. Нахождение функции регрессии с помощью теории планирования эксперимента Цель занятия: ознакомиться с оптимальным планом машинного эксперимента над математической моделью, определить с помощью средств Mathcad функцию регрессии и исследовать функцию регрессии на экстремум по оптимальному плану. Задана физическая модель, зависящая от трех независимых параметров x, y, z (вид зависимости получен из уравнения  Рис. 1. Листинг программы Новая базовая точка (x1, y1, z1) находится с учетом направления возрастания функции регрессии f2(x1, y1, z1). Полученные значения новой базовой точки подставляются в начальные значения, то есть x0= x1, y0= y1, z0= z1, копируются и переносятся в начало программы, а старые значения x0, y0, z0 предварительно удаляются. Расчет повторяется несколько раз, пока относительная разность величин (f2(x1, y1, z1) - f2(x0, y0, z0)) / f2(x1, y1, z1) не станет по меньше 0.01, а результаты после замены x0= x1, y0= y1, z0= z1 и подстановки вместо старых значений копируются и вставляются в виде рисунка в отчет. На рис. 2 показаны все результаты расчета для варианта №1. Р 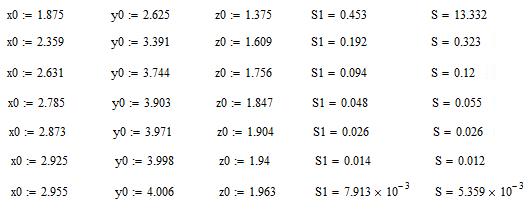 ис. 2. Результаты последовательного поиска оптимальных параметров с помощью теории планирования эксперимента Выводы: как видно из рис. 2, для исходных значений параметров x0 = 1, y0 = 1, z0 = 1 достижение относительного приращения функции регрессии S < 0.01 происходит за 7 поисков из новых точек. Функция S в зависимости от номера поиска ведет себя нелинейно, но стремится к 0 по модулю. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №6 Построение алгоритма расчета вихревого энергоразделителя с использованием корреляционного метода итераций. Исследование модели вихревого энергоразделителя численным методом Цель занятия: ознакомиться с методами исследования математической модели технического устройства с использованием корреляционного метода итераций. Из-под программы Just BASIC v2.0.exe запускалась программа Prak_zan-6.bas для расчета характеристик вихревого энергоразделителя. Находилась строка «Dr = .15» и заменялась на строку «Dr = 1/100», где цифра «2» соответствует номеру варианта. После запуска счета и получения результатов произведено их копирование и вставка в отчет в виде текста. После выделения текста в ВОРДе производилось его преобразование в таблицу с помощью пункта меню «Вставка | Таблица | Преобразовать в таблицу», где в качестве разделителя был указан пробел. Предварительно удалялись лишние пробелы так, чтобы между числами оставался только один пробел. Если число итераций S или J были больше максимально установленного предела (100 для S и 10000 для J), то расчетные величины корректировались так, чтобы число, значительно большее мо модулю 1, заменялось на 1. После удаления лишних столбцов остался результат, показанный в виде таблицы 1. Таблица 1 – результаты расчета характеристик вихревого энергоразделителя при Dr = 1/100
И 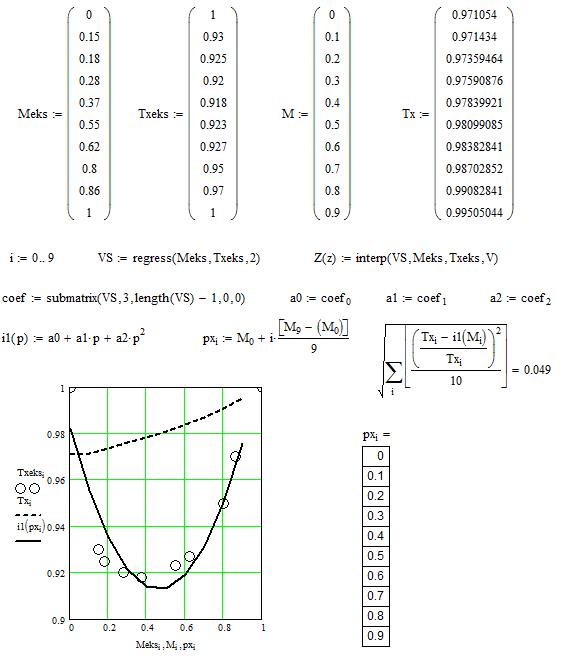 з-под программы Mathcad.exe запускалась программа Prak_zan-6.mcdx для аппроксимации экспериментальных данных по вихревому энергоразделителю и определению расхождения с расчетными данными. Результаты вычислений копировались из столбца «Tx/T1» таблицы 1 и вставлялись в столбец матрицы «Тх» файла Prak_zan-6.mcd, результат выполнения этого файла представлен на рис. 1. Рис. 1. Результаты аппроксимации экспериментальных данных по вихревому энергоразделителю и определения расхождений с расчетными данными Как видно из рис. 1, среднеквадратичное отклонение экспериментальных данных по вихревому энергоразделителю от расчетных данных составило В=0.049 или 4,9%. Сумма данных столбца «S» таблицы 1, которые представляют число итераций корреляционного метода итераций первого цикла, составила 126. Сумма данных столбца «J» таблицы 1, которые представляют число итераций корреляционного метода итераций второго цикла, составила 1573. Суммы данных подсчитывались с помощью электронной таблицы EXCEL – файл Prak_zan-6.xlsx. В программе Prak_zan-6.bas были изменены следующие строки: вместо «KOR1 = 1.3» стало «KOR1 = 1.3*1.5», вместо «KOR2 = .8» стало «KOR2 = .8*0.9», вместо «Dr = 1/100» стало «Dr = 1/100*1.5», то есть коэффициент корреляции первого итерационного цикла KOR1 был увеличен на 50%, коэффициент корреляции второго итерационного цикла KOR2 был уменьшен на 10%, а коэффициент дросселирования Dr был увеличен на 50%. После получения результатов нового расчета и преобразований их в таблицу получена таблица 2. Таблица 2 – результаты расчета характеристик вихревого энергоразделителя при Dr = 1/100*1.5
Результаты вычислений копировались из столбца «Tx/T1» таблицы 2 и вставлялись в столбец матрицы «Тх» файла Prak_zan-6.mcdx, результат выполнения этого файла представлен на рис. 2. 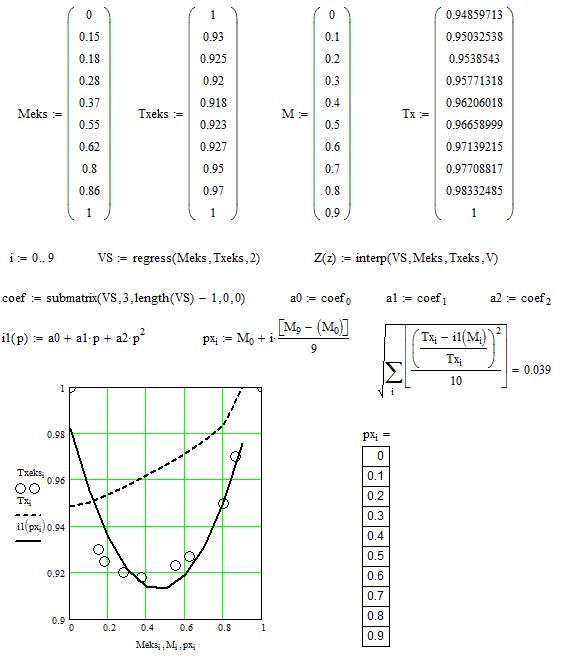 Рис. 2. Результаты аппроксимации экспериментальных данных по вихревому энергоразделителю и определения расхождений с новыми расчетными данными Как видно из рис. 2, среднеквадратичное отклонение экспериментальных данных по вихревому энергоразделителю от расчетных данных составило В=0.039 или 3,9%. Сумма данных столбца «S» таблицы 2, которые представляют число итераций корреляционного метода итераций первого цикла, составила 167. Сумма данных столбца «J» таблицы 1, которые представляют число итераций корреляционного метода итераций второго цикла, составила 595. Выводы: увеличение коэффициента корреляции первого итерационного цикла KOR1 на 50% увеличивает суммарное число итераций со 126 до 167, снижение коэффициента корреляции второго итерационного цикла KOR2 на 10% снижает суммарное число итераций с 1573 до 595, повышение коэффициента дросселирования Dr на 50% понижает среднеквадратичное отклонение экспериментальных данных по вихревому энергоразделителю от расчетных данных с 4,9% до 3,9%. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №7 Моделирование системы технического обслуживания грузовых вагонов с целью определения оптимальной периодичности плановых ремонтов. Исследование модели системы технического обслуживания грузовых вагонов численным методом Цель занятия: овладеть навыками нахождения экстремумов функции в Бейсике на примере решения оптимизационной задачи определения оптимальной периодичности плановых видов ремонта вагона. В таблице 1 заданы начальные значения х0, y0, z0 для варианта №3. Данные для других вариантов берутся из табл. 8 методических указаний №4954. Таблица 1
И 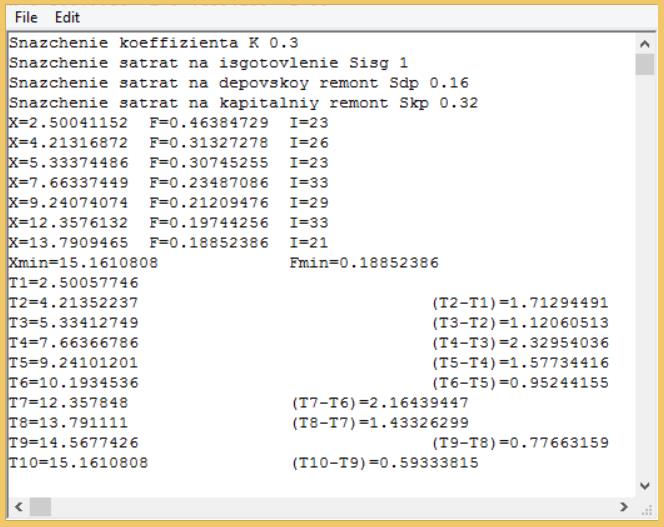 з-под программы Just BASIC v2.0.exe запускалась программа Prak_zan-7.bas для расчета оптимальной периодичности плановых видов ремонта вагона. В ходе выполнения программы задавались значения «К» - К, «Sisg» - Сизг, «Sdp» - Сдр, «Skp» - Скр. Результаты расчетов представлены на рис.2. Рис. 1. Результаты расчета предельного срока службы вагона и оптимальных межремонтных периодов Выводы: Предельный срок службы вагона равен Xmin=15,16 года. Определены оптимальные межремонтные сроки: - между началом эксплуатации и первым деповским ремонтом Т1=2,5 года; - между первым и вторым деповским ремонтом (Т2-Т1)=1,71 года; - между вторым и третьим деповским ремонтом (Т3-Т2)=1,12 года; - между первым капитальным и четвертым деповским ремонтом (Т4-Т3)=2,33 года; - между четвертым и пятым деповским ремонтом (Т5-Т4)=1,58 года; - между пятым и шестым деповским ремонтом (Т6-Т5)=0,95 года; - между вторым капитальным и седьмым деповским ремонтом (Т7-Т6)=2,16 года; - между восьмым и седьмым деповским ремонтом (Т8-Т7)=1,43 года; - между девятым и восьмым деповским ремонтом (Т9-Т8)=0,78 года; - между десятым и девятым деповским ремонтом (Т10-Т9)=0,59 года. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №8 Составление математической модели вихревого энергоразделителя с помощью программы СААМ. Исследование модели вихревого энергоразделителя в программе СААМ Цель занятия: ознакомиться с методами математического моделирования с использованием программы СААМ на примере составления аналоговой математической модели вихревого энергоразделителя. Исходные данные взяты из табл. 9 методических указаний № 4954 и занесены в табл. 1. Таблица 1 – Исходные данные
После запуска программы «Вихревая труба.caam» в среде СААМ вызывается «Редактор кода» правой кнопкой мыши на стрелке элемента «Исток» («Source 1»). Текущие параметры давления и температуры менялись на величины, заданные по варианту. Доля холодного газа μ, заданная по варианту устанавливалась для параметра «доля выхода» в «Редакторе кода», вызываемом правой кнопкой мыши на выходной соединенной стрелке элемента «Amalgamator 1». В «Редакторе кода», вызываемом правой кнопкой мыши на выходной свободной стрелке элемента «Amalgamator 1», для параметра «доля выхода» устанавливается значение (1 – μ), что соответствует доле горячего газа. В «Редакторе кода», вызываемом правой кнопкой мыши на входной стрелке элемента «Сток» («Drain 1»), устанавливается значение давления, заданное по варианту. После запуска счета для просмотра свойств объектов вызывается «Инспектор объектов» правой кнопкой мыши на входной стрелке элемента «Сток» («Drain 1»). Расчетное значение температуры было сильно меньше опытного значения температуры холодного потока, заданного по варианту, поэтому необходимо было изменить значение характеристики дросселя «Drossel 1». Для этого в «Редакторе кода», вызываемом правой кнопкой мыши на выходной стрелке элемента «Drossel 1», для параметра «доля выхода» устанавливалось значение, меньше первоначального, однако, расчетное значение температуры увеличивалось незначительно, оставаясь сильно меньше опытного значения температуры холодного потока. Поэтому в аналоговую схему вихревого энергоразделителя были добавлены два элемента: «Amalgamator 2» и «Amalgamator 3», для имитации перетока газа с температурой на входе в выходной холодный поток. Для параметра «доля потока» вертикальной выходной стрелки элемента «Amalgamator 2» устанавливалось значение 0.07, а для параметра «доля потока» горизонтальной выходной стрелки элемента «Amalgamator 2» устанавливалось значение 0.93. Чтобы доля холодного потока оставалась равной заданной величины μ=0.15, для параметра «доля выхода» на выходной свободной стрелке элемента «Amalgamator 1» устанавливалось значение (1 – μ)/0.93 0.914, а для соединенной выходной стрелки – значение параметра «доля выхода» (1 – 0.914) = 0.086. В «Редакторе кода», вызываемом правой кнопкой мыши на выходной стрелке элемента «Drossel 1», для параметра «доля выхода» устанавливалось значение 0.0924, при этом происходила остановка счета по внутренней ошибке. Чтобы устранить ошибку, в данном элементе изменялось значение коэффициента корреляции итерационного процесса расчета, например, вместо К = 0.3 принималось значение, большее 1, а именно К = 1.3 или близкое к 0, например, Л = 0.1. Для этого не на стрелках, а на самом элемента правой копкой мыши в 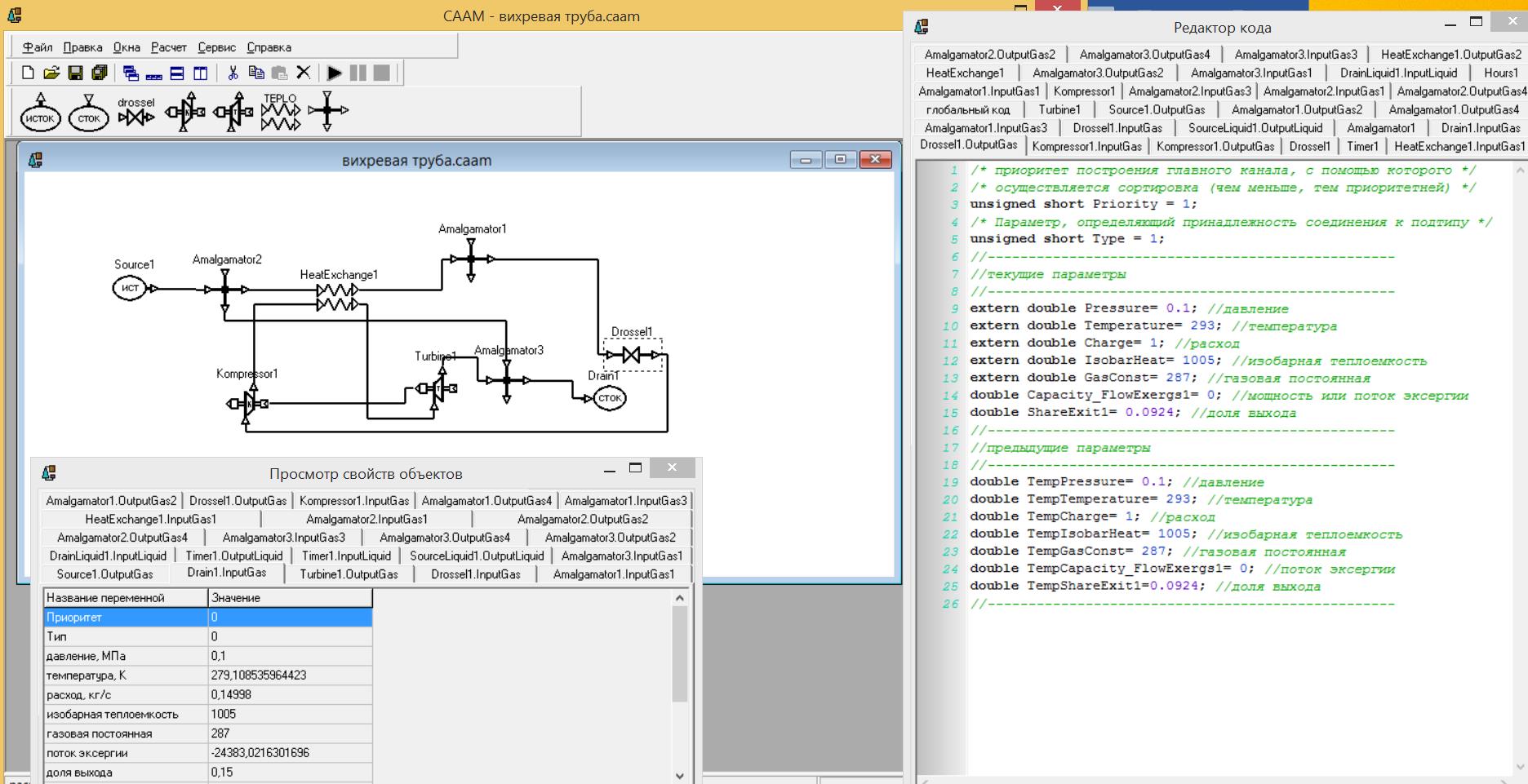 ызывался «Редактор кода». На рис. 1 представлены результаты расчета. Рис. 1. Результаты расчета температуры холодного потока Как видно на рис. 1, расчетное значение температуры холодного потока совпадает с экспериментальным значением, заданным по варианту. Выводы: чтобы добиться совпадения расчетного значения температуры холодного потока с экспериментальным значением, необходимо в аналоговой схеме вихревого энергоразделителя добавить два элемента: «Amalgamator 2» и «Amalgamator 3» для имитации перетока газа с температурой на входе в выходной холодный поток и долей перетекающего газа 0.07; значение коэффициента дросселирования должно быть 0.0924; коэффициенты корреляции итерационных процессов должны быть больше 1. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №9 Составление математической модели цистерны для вязких жидкостей с теплоизолирующим кожухом с помощью программы СААМ. Исследование модели цистерны для вязких жидкостей в программе СААМ Цель занятия: получить представление о методах объектно-ориентированного программирования в среде визуального программирования СААМ на примере моделирования процесса перевозки мазута в железнодорожной цистерне. Исходные данные взяты из табл. 10 методических указаний № 4954 и занесены в табл. 1. Таблица 1 – Исходные данные
После запуска программы «Охлаждение мазута-таймер.caam» в среде СААМ вызывается «Редактор кода» правой кнопкой мыши на стрелке элемента «Исток» («SourceLiquid 1»). Текущие параметры начальной температуры мазута и отношения температуры жидкости к температуре окружающей среды в начале перевозки менялись на величины, заданные по варианту. В «Редакторе кода», вызываемом правой кнопкой мыши на входной стрелке элемента «Сток» («DrainLiquid 1»), устанавливается значение отношения температуры жидкости к температуре окружающей среды в конце перевозки, заданное по варианту. В «Редакторе кода», вызываемом правой кнопкой мыши на элементе «Hours 1», устанавливается значение Dtau = 3600*96, что соответствует времени перевозки, переведенному в секунды. После запуска счета для просмотра свойств объекта вызывается «Инспектор объектов» правой кнопкой мыши на входной стрелке элемента «Сток» («DrainLiquid 1»). Результаты расчета представлены на рис. 1. 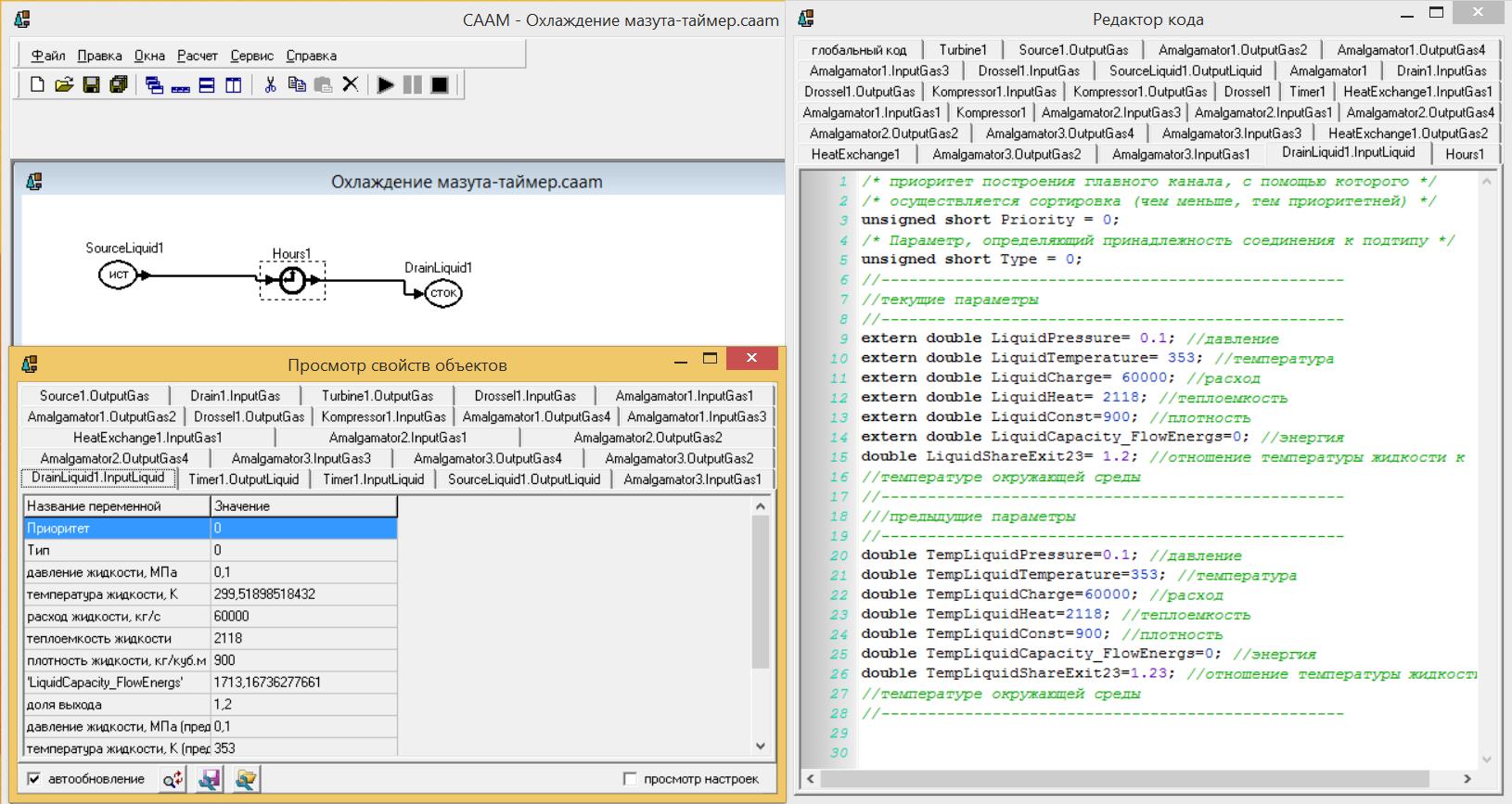 Рис. 1. Результаты расчета температуры мазута в конце перевозки Как видно на рис. 1, температуры мазута в конце перевозки составила 299.5 К. |
