параллельный поиск минимального и максимального элементов в двумерном целочисленном массиве с применением технологии openmp. пр2 пп Еременко. Отчет по практической работе 2 по дисциплине Параллельное программирование
 Скачать 375.42 Kb. Скачать 375.42 Kb.
|
Институт Информационных технологий Кафедра Математического обеспечения и стандартизации информационных технологий
Москва 2021 Цель работыОтработка принципов распараллеливания программ; Реализация простейшей многопоточной программы; Анализ эффективности параллельной программы по сравнению с последовательной программой. Постановка задачиСоставить программу, реализующую распараллеленное вычисление, согласно индивидуальному варианту. Провести ручное тестирование программы на небольшом объеме входных данных. Результаты тестирования в виде скриншотов экранов включить в отчет по выполненной работе. Провести контрольные прогоны программы для нескольких разных значений параметра n и установленных количествах потоков p = 1, 2, 4, 8, 16, 32 и 64. В индивидуальном варианте задания приведены рекомендуемые параметры n. Значения параметра nможно переопределить самостоятельно таким образом, чтобы уменьшить относительную погрешность результатов. Результаты прогонов в виде скриншотов экранов включить в отчет по выполненной работе. Полученные результаты свести в сводную таблицу. Вычислить показатели ускорения, эффективности и стоимости параллельной реализации программы. Построить графики времени выполнения, изменения ускорения, эффективности и стоимости параллельной реализации в зависимости от параметра p. Провести анализ полученных результатов. Сделать выводы о проделанной работе, основанные на полученных результатах. Оформить отчет с подробным описанием разработанной программы, принципов программной реализации распараллеленной обработки данных, описанием текста исходного кода и проведенного тестирования программы. Вариант №9. Условие задания: Составить программу, реализующую последовательный и параллельный поиск минимального и максимального элементов в двумерном целочисленном массиве A[n,n]. Провести тестирование программы на массиве размером n = 5, сформированном вводом с клавиатуры. Рабочий массив А сформировать, используя генератор псевдослучайных чисел. Провести контрольные прогоны программы для размеров n = 100, 500, 1000, 1500, 2000. Решение Для нахождения минимального и максимального значения в двумерном массиве необходим вложенный цикл, который будет проходить по каждому элементу массива и путем сравнения с переменными находить требуемые величины. Этот вложенный цикл должен быть распараллелен. Для создания параллельных циклов используется директива #pragma omp for. Она создает в параллельной области параллельный цикл и распределяет итерации цикла по потокам. Точкой синхронизации потоков (барьером) по умолчанию является конец цикла. Опция private устанавливает локальные переменные каждому потоку на все время его существования. Для анализа эффективности параллельной программы необходимо ознакомиться с показателями эффективности параллельных программ. Показатели эффективности параллельного алгоритма Ускорение; Эффективность; Стоимость. Ускорение (speedup), получаемое при использовании параллельного алгоритма для p потоков, по сравнению с последовательным вариантом выполнения вычислений определяется величиной 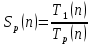 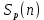 – это отношение времени последовательного выполнения программы к времени параллельного выполнения программы Величина n применяется для параметризации вычислительной сложности решаемой задачи и может пониматься, к примеру, как размер входных данных задачи. – это отношение времени последовательного выполнения программы к времени параллельного выполнения программы Величина n применяется для параметризации вычислительной сложности решаемой задачи и может пониматься, к примеру, как размер входных данных задачи.Эффективность (efficiency) использования параллельным алгоритмом ресурсов компьютера (процессоров, ядер или потоков) при решении задачи определяется соотношением 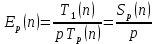 Величина эффективности определяет среднюю долю времени выполнения алгоритма, в течение которой процессоры (ядра или потоки) реально задействованы для решения задачи. Из приведенных соотношений можно показать, что в наилучшем случае 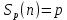 и и 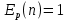 . .При выборе надлежащего параллельного способа решения задачи может оказаться полезной оценка стоимости (cost) вычислений, определяемой как произведение времени параллельного решения задачи и числа используемых процессоров 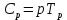 В связи с этим можно определить понятие стоимостно-оптимального (cost-optimal) параллельного алгоритма как метода, стоимость которого является пропорциональной времени выполнения наилучшего последовательного алгоритма. Функция parallel_sort реализует нахождение максимального и минимального значения в двумерном массиве. Значение min инициализируется 30000, max- 0. Для прохождения по всем элементам двумерного массива необходим основной и вложенный цикл. Вложенный цикл проходится по всем элементам массива. Именно этот цикл и будет распараллеливаться. В этом цикле происходит сравнение актуального минимального и максимального значения с каждым элементом массива, при удовлетворении операции сравнения происходит присвоение минимальной или максимальной переменной значения элемента массива. Алгоритм завершает свою работу при сравнении со всеми элементами массива.
Пользователю на выбор предлагается два варианта: заполнение массива вручную для проверки правильности алгоритма и заполнение массива при помощи генератора случайных чисел. Если пользователь выбирает первый вариант, то ему необходимо ввести 25 элементов массива. Для автоматического теста программа выведет размерность массива, количество потоков, время, затраченное на поиск минимального и максимального значений, минимальное и максимальное значение и данные для аналитики: стоимость, ускорение, эффективность. Для ручного теста будут выведены время, затраченное на сортировку, изначальный массив, максимальное и минимальное значение.  Рис. 1 Интерфейс программы ТестированиеДля тестового прогона программы пользователь вручную заполняет двумерный массив из 25 элементов. 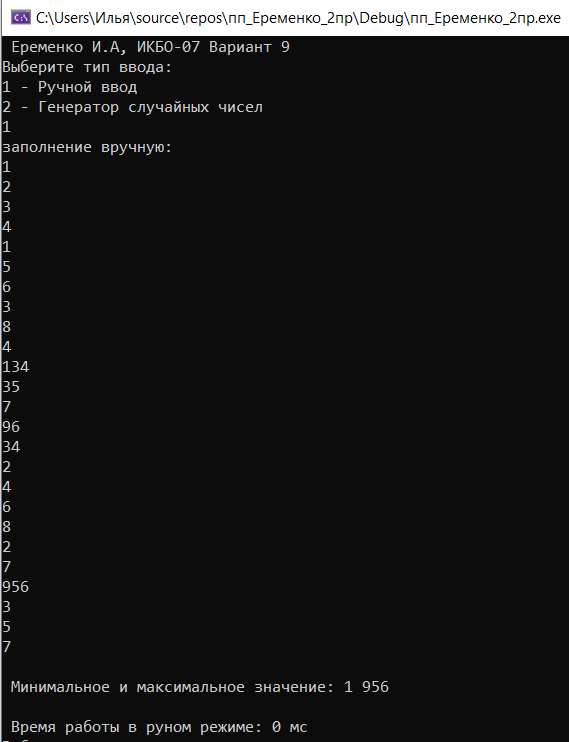 Рис. 2 Тестовый прогон Рабочий прогон программы проводится для массивов размерностью nxn, где n = 100, 500, 1000, 1500 и 2000. Они заполняются случайными целыми числами в диапазоне от 0 до 30000. К каждому из них применяется поиск минимального и максимального значения с количеством потоков: 1, 2, 4, 8, 16, 32, 64. Для каждого массива с разными размерностями и поточностью высчитываются и выводятся: размерность массива, количество потоков, время, затраченное на поиск минимального и максимального значений, минимальное и максимальное значение и данные для аналитики: стоимость, ускорение, эффективность. 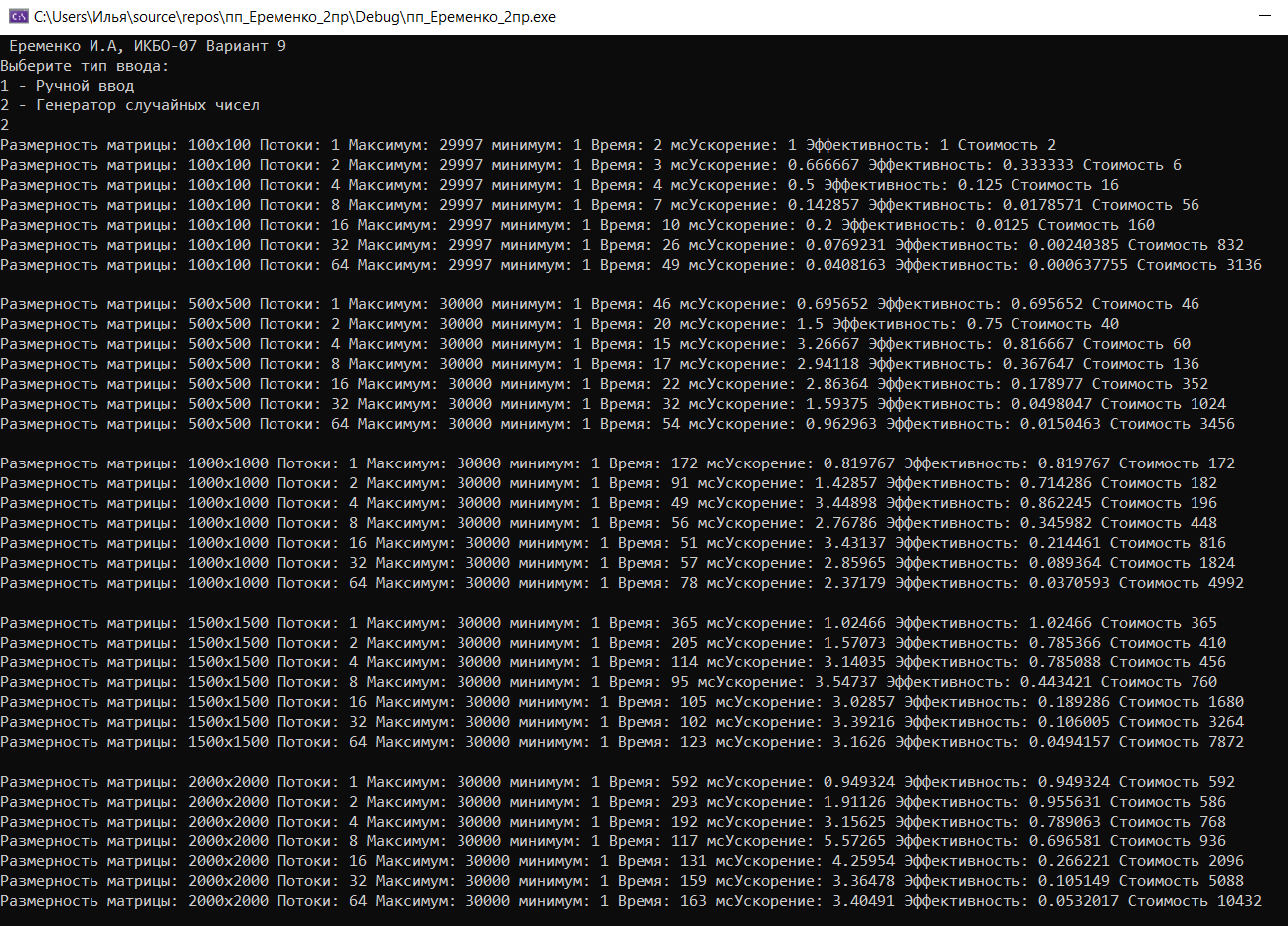 Рис. 3 Рабочий прогон На основе полученных данных заполним таблицы и построим графики для различных n. Таблица 1. Рабочий прогон (n = 100)
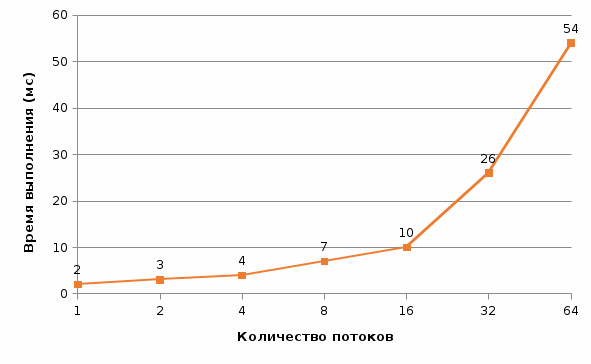 Рис. 4 График времени выполнения от количества потоков (n = 100) 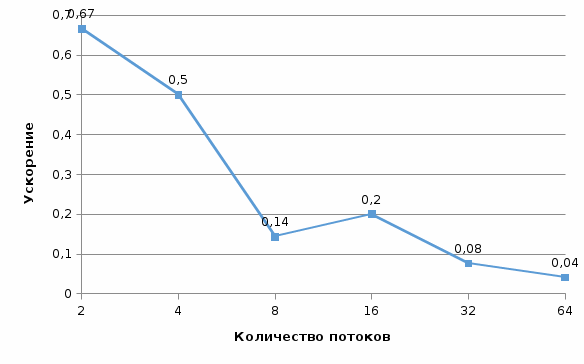 Рис. 5 График ускорения от количества потоков (n = 100) Рис. 5 График ускорения от количества потоков (n = 100)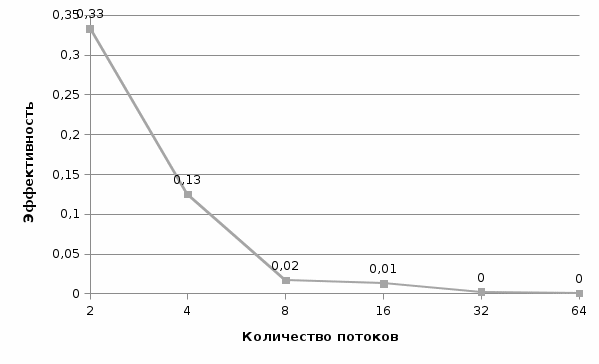 Рис. 6 График эффективности от количества потоков (n = 100) Рис. 6 График эффективности от количества потоков (n = 100)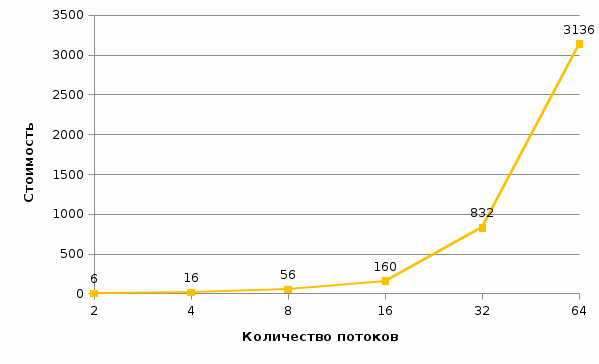 Рис. 7 График стоимости от количества потоков (n = 100) Рис. 7 График стоимости от количества потоков (n = 100)Таблица 2. Рабочий прогон (n = 500)
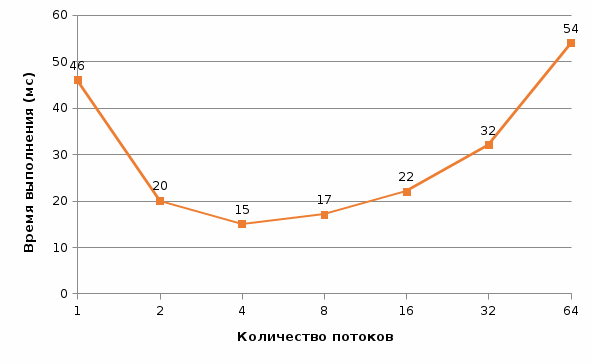 Рис. 8 График времени выполнения от количества потоков (n = 500) Рис. 8 График времени выполнения от количества потоков (n = 500)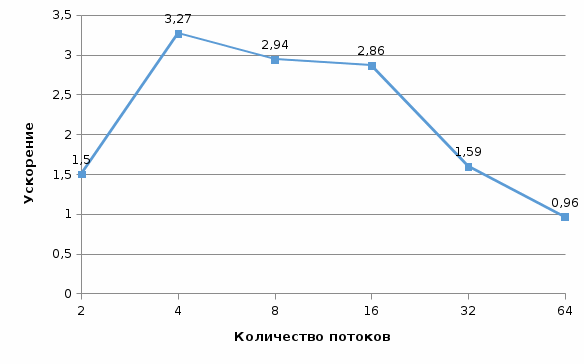 Рис. 9 График ускорения от количества потоков (n = 500) Рис. 9 График ускорения от количества потоков (n = 500)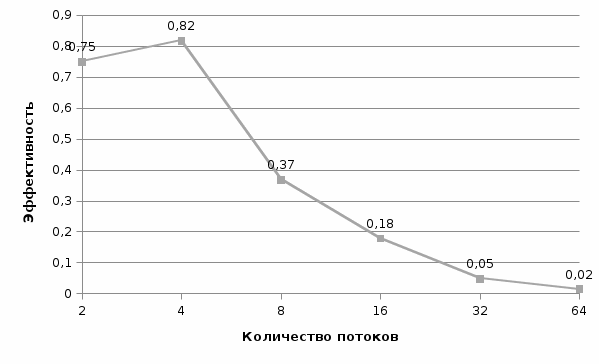 Рис. 10 График эффективности от количества потоков (n = 500) Рис. 10 График эффективности от количества потоков (n = 500)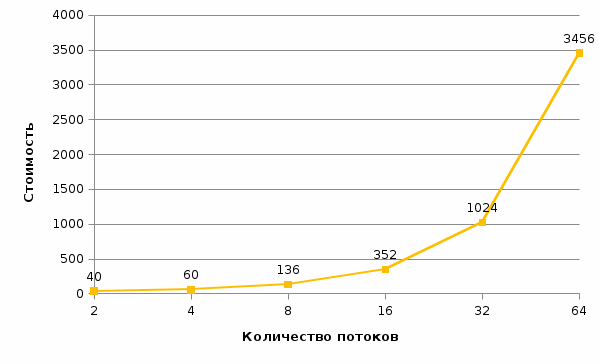 Рис. 11 График стоимости от количества потоков (n = 500) Рис. 11 График стоимости от количества потоков (n = 500)Таблица 3. Рабочий прогон (n = 1000)
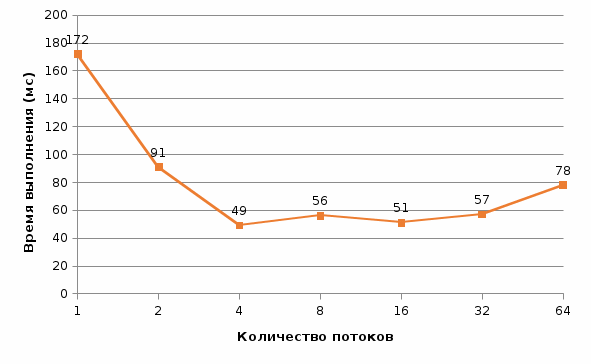 Рис. 12 График времени выполнения от количества потоков (n = 1000) Рис. 12 График времени выполнения от количества потоков (n = 1000)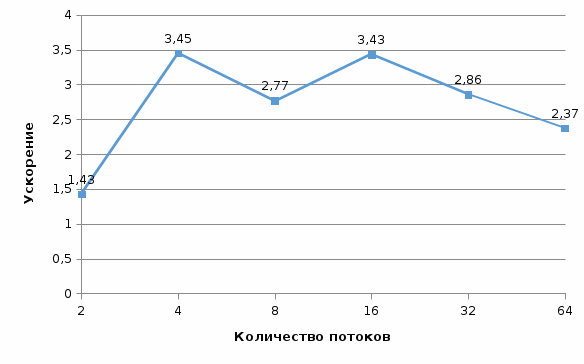 Рис. 13 График ускорения от количества потоков (n = 1000) Рис. 13 График ускорения от количества потоков (n = 1000)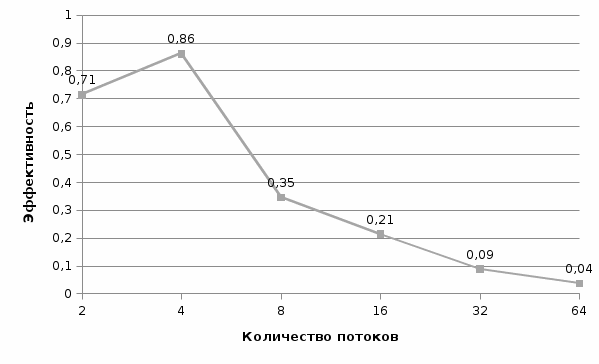 Рис. 14 График эффективности от количества потоков (n = 1000) Рис. 14 График эффективности от количества потоков (n = 1000)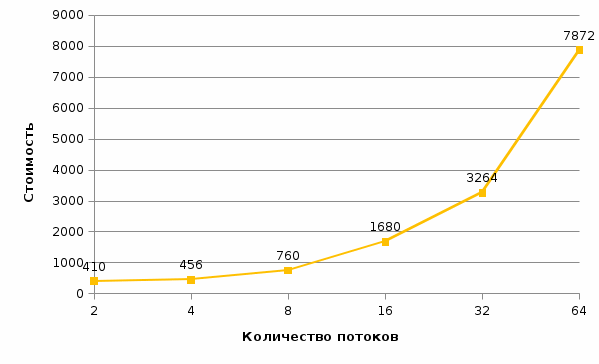 Таблица 4. Рабочий прогон (n = 1500)
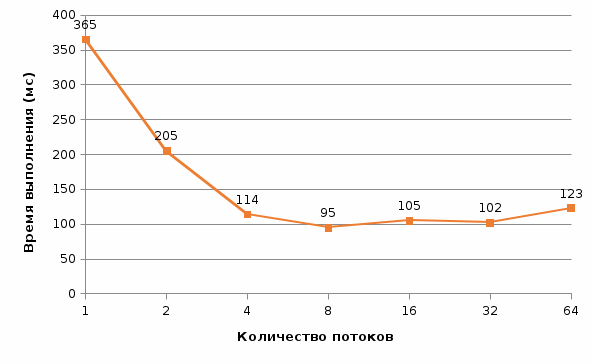 Рис. 15 График времени выполнения от количества потоков (n = 1500) Рис. 15 График времени выполнения от количества потоков (n = 1500)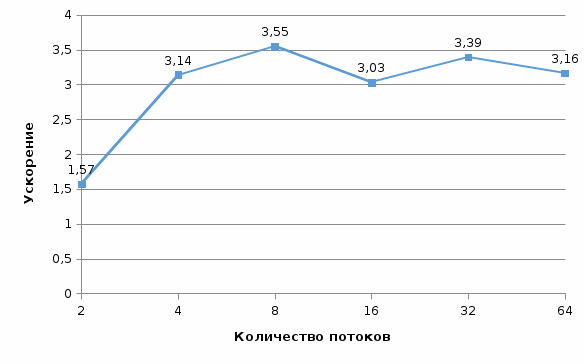 Рис. Рис. 16 График ускорения от количества потоков (n = 1500) Рис. Рис. 16 График ускорения от количества потоков (n = 1500)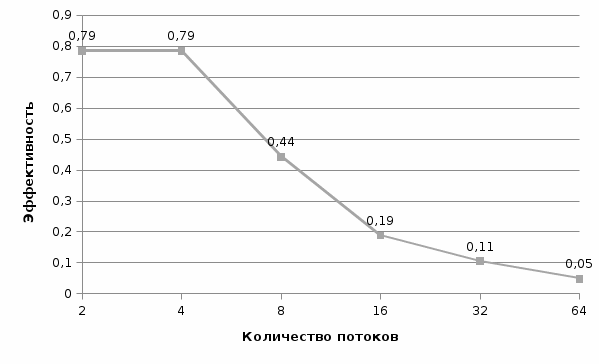 Рис. 17 График эффективности от количества потоков (n = 1500) Рис. 17 График эффективности от количества потоков (n = 1500)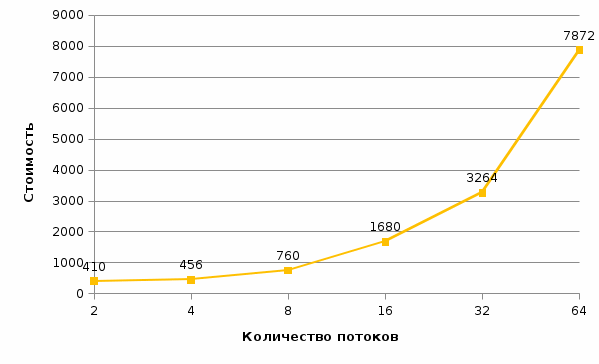 Рис. 18 График стоимости от количества потоков (n = 1500) Рис. 18 График стоимости от количества потоков (n = 1500)Таблица 5. Рабочий прогон (n = 2000)
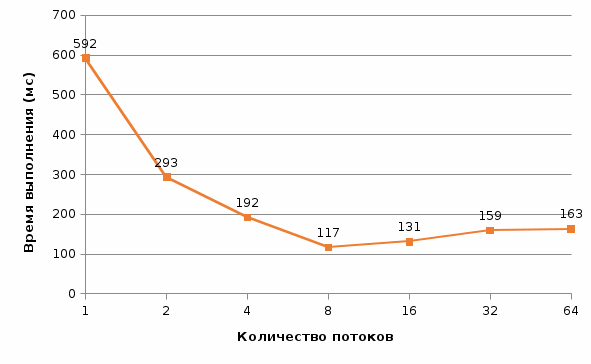 Рис. 19 График времени выполнения от количества потоков (n = 2000) Рис. 19 График времени выполнения от количества потоков (n = 2000)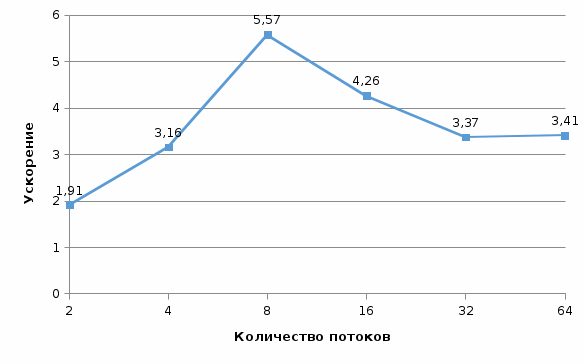 Рис. 20 График ускорения от количества потоков (n = 2000) Рис. 20 График ускорения от количества потоков (n = 2000)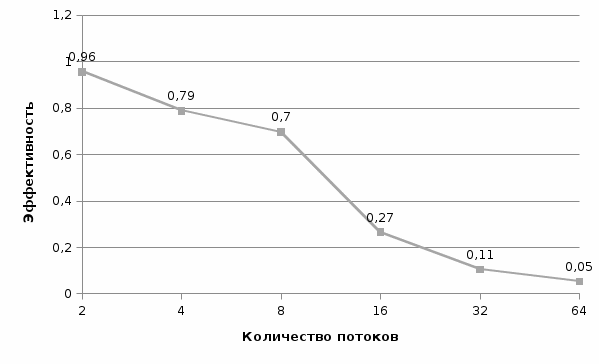 Рис. 21 График эффективности от количества потоков (n = 2000) Рис. 21 График эффективности от количества потоков (n = 2000)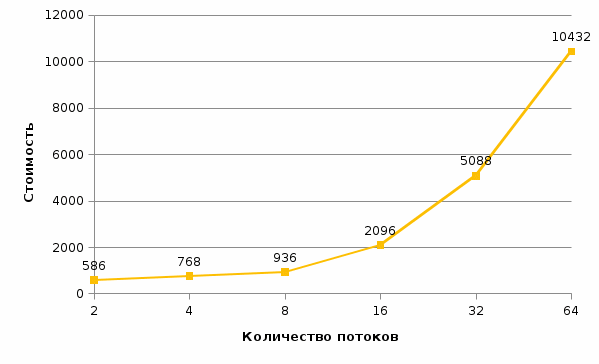 Рис. 22 График стоимости от количества потоков (n = 2000) Рис. 22 График стоимости от количества потоков (n = 2000)Из результатов выполнения программы видно: При росте числа потоков снижается прирост ускорения. Начиная с некоторого количества потоков, прирост ускорения становится отрицательным, и программа начинает работать медленнее, чем с меньшим количеством потоков. При этом, чем меньше n, тем меньшее количество потоков для этого необходимо. На малом кол-ве данных распараллеливание не ускоряет работу алгоритма. ВыводВ результате выполнения работы я: Научился программировать параллельные циклы средствами OpenMP; Научился рассчитывать показатели эффективности параллельных программ. Проанализировал полученные данные и сделал выводы Исходный код программы
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

