рб. практическая работа 6. Отчет по практической работе 6 Построение комбинационных схем, реализующих мднф и мкнф заданной логической функции от 4х переменных в базисах
 Скачать 340.52 Kb. Скачать 340.52 Kb.
|
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования "МИРЭА - Российский технологический университет" РТУ МИРЭА  Институт кибернетики Кафедра общей информатики ОТЧЕТ ПО ПРАКТИЧЕСКОЙ РАБОТЕ №6 Построение комбинационных схем, реализующих МДНФ и МКНФ заданной логической функции от 4-х переменных в базисах «И-НЕ», «ИЛИ-НЕ» по дисциплине «ИНФОРМАТИКА»
Москва 2022 СодержаниеРТУ МИРЭА 1 ОТЧЕТ 1 Построение комбинационных схем, реализующих МДНФ и МКНФ заданной логической функции от 4-х переменных в базисах «И-НЕ», «ИЛИ-НЕ» 1 по дисциплине 1 1.ПОСТАНОВКА ЗАДАЧИ 3 2.ПРОЕКТИРОВАНИЕ И РЕАЛИЗАЦИЯ 4 2.1СОСТАВЛЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ 4 2.2МИНИМИЗАЦИЯ ЛОГИЧЕСКОЙ ФУНКЦИИ С ПОМОЩЬЮ КАРТ КАРНО 5 2.3ПРИВЕДЕНИЕ МДНФ И МКНФ К БАЗИСАМ «И-НЕ» И 6 «ИЛИ-НЕ» 6 2.4ПОСТРОЕНИЕ СХЕМ 6 3.ВЫВОДЫ 10 4.СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 11 ПОСТАНОВКА ЗАДАЧИЛогическая функция от четырех переменных задана в 16-теричной векторной форме. Восстановить таблицу истинности. Минимизировать логическую функцию при помощи карт Карно и получить формулы МДНФ и МКНФ в общем базисе. Перевести МДНФ и МКНФ в базисы «И-НЕ» и «ИЛИ-НЕ» (каждую минимальную форму в два базиса). Построить комбинационные схемы для приведенных к базисам формул МДНФ и МКНФ в лабораторном комплексе, используя только логические элементы, входящие в конкретный базис. Протестировать работу схем и убедиться в их правильности Личный код – 26010. ПРОЕКТИРОВАНИЕ И РЕАЛИЗАЦИЯСОСТАВЛЕНИЕ ТАБЛИЦЫ ИСТИННОСТИФункция имеет вид: 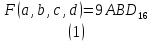 Преобразуем ее в двоичную запись: 1001 1010 1011 1101 – получили столбец значений логической функции, который необходим для восстановления полной таблицы истинности (см. табл. 1). Таблица 1 – Таблица истинности для функции F
МИНИМИЗАЦИЯ ЛОГИЧЕСКОЙ ФУНКЦИИ С ПОМОЩЬЮ КАРТ КАРНОСоставим МДНФ заданной функции (логическая формула (2)). Для этого воспользуемся методом Карт Карно (см. рис. 1)
Рисунок 1 - Карта Карно, заполненная для построения МДНФ 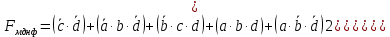 Составим МКНФ заданной функции (логическая формула (3)). Для этого воспользуемся методом Карт Карно (см. рис. 2)
Рисунок 2 - Карта Карно, заполненная для построения МКНФ 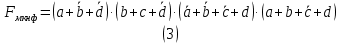 ПРИВЕДЕНИЕ МДНФ И МКНФ К БАЗИСАМ «И-НЕ» И«ИЛИ-НЕ»Приведем полученные МДНФ к базисам «И-НЕ» и «ИЛИ-НЕ» (логические формулы (4) и (5) соответственно) и МКНФ к базисам «И-НЕ» и «ИЛИ-НЕ» (логические формулы (6) и (7) соответственно). Для этого воспользуемся законами де-Моргана. 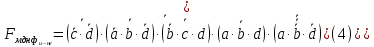 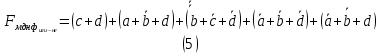 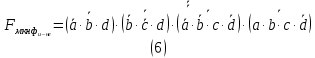 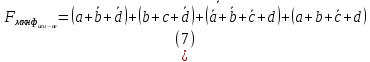 ПОСТРОЕНИЕ СХЕМПостроим в лабораторном комплексе схемы МДФН в базисе «И-НЕ» (см. рис. 3) и в базисе «ИЛИ-НЕ» (см. рис. 4), а также МКНФ в базисе «И-НЕ» (см. рис. 5) и в базисе «ИЛИ-НЕ» (см. рис. 6) и убедимся в их правильности.  Рисунок 3 – Схема МДНФ в базисе «И-НЕ» 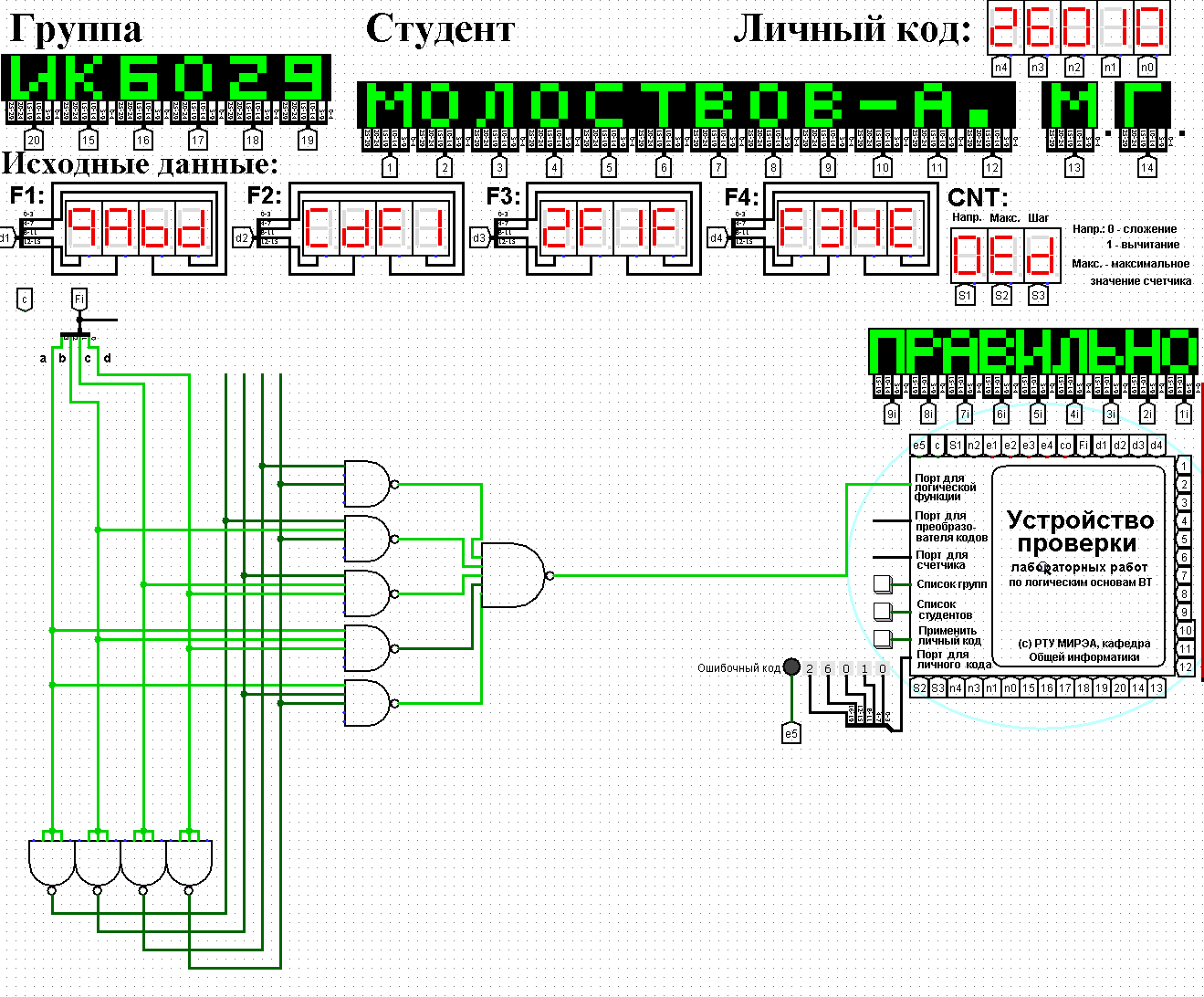  Рисунок 4 – Схема МДНФ в базисе «ИЛИ-НЕ» 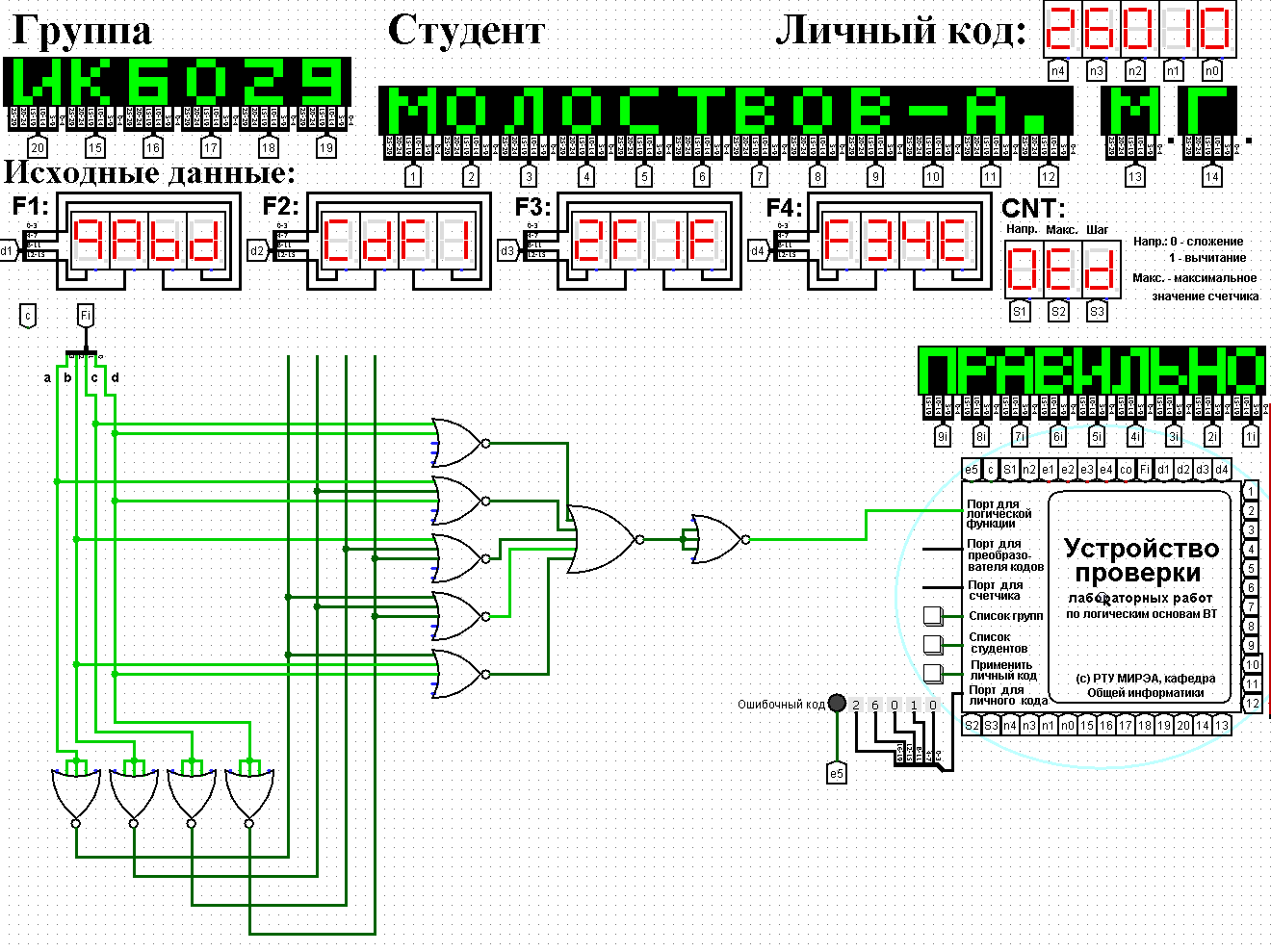   Рисунок 5 – Схема МКНФ в базисе «И-НЕ»  Рисунок 6 – Схема МКНФ в базисе «ИЛИ-НЕ» 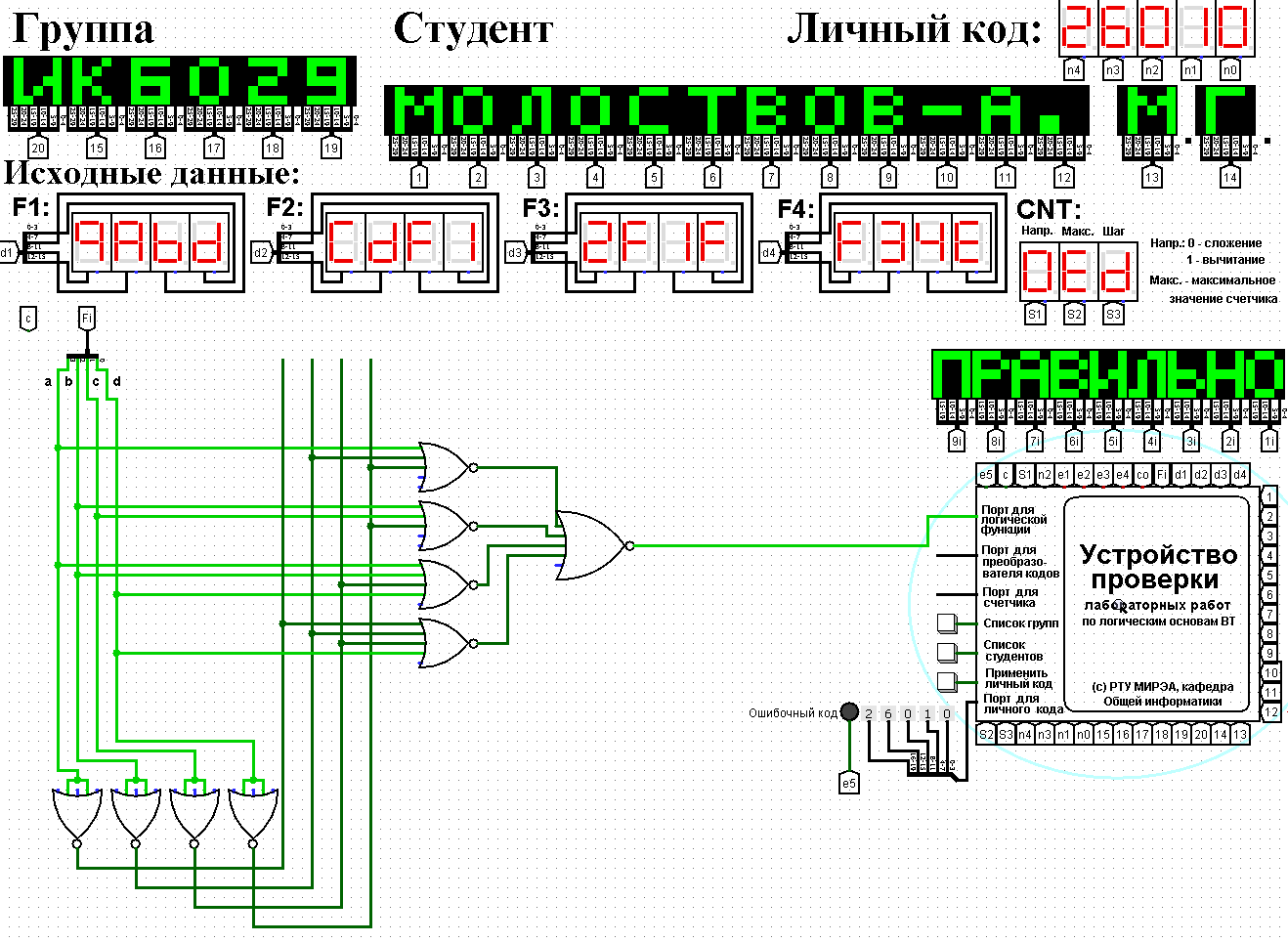 ВЫВОДЫБыла восстановлена таблица истинности логической функции от четырех переменных, заданной в 16-ричной векторной форме. При помощи карт Карно минимизирована логическая функция и получены формулы МДНФ и МКНФ в общем базисе. МДНФ и МКНФ переведены в базисы «И-НЕ» и «ИЛИ-НЕ». Построены комбинационные схемы в лабораторном комплексе. Освоено построение карт Карно и построение схем из логических элементов «И-НЕ» и «ИЛИ-НЕ». СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВИнформатика. Методические указания по выполнению практических работ для студентов. С.С. Смирнов, Д.А. Карпов, МИРЭА Российский технологический университет, -М., 2021. - 102 с. эл.изд |


 1
1
 1
1 1
1

 0
0 0
0