ПР1_Бабий_Д_С. Отчет по работе добавить ответы на вопросы к защите (файл Пример Практика 1)
 Скачать 322.01 Kb. Скачать 322.01 Kb.
|
|
Федеральное государственное автономное образовательное учреждение высшего образования «СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» Институт космических и информационных технологий Цифровые технологии управления ОТЧЁТ О ПРАКТИЧЕСКОЙ РАБОТЕ №1 СНИЖЕНИЕ РАЗМЕРНОСТИ ПРИЗНАКОВ МЕТОД ГЛАВНЫХ КОМПОНЕНТ ВАРИАНТ 2 Преподаватель _________ А.В. Федорова подпись, дата Студент КИ19-23Б, 071940830 __________ Д.С. Бабий подпись, дата Красноярск 2020 Цель: изучить метод главных компонент, провести снижение размерности признаков. Постановка задачи Исходными данными являются выборочные данные по 53 предприятиям машиностроительного комплекса, характеризующимся 14-ю показателями производственно-хозяйственной деятельности (файл «Исходные данные 2»). На основе выборочных данных из генеральной совокупности и согласно вашему варианту (файл Исходные данные 2 - последняя страница) X=(Xi1, Xi2, Xi3, Xi4, Xi5), используя возможности языка «Python», провести понижение размерности данных, используя метод главных компонент: С помощью компонентного анализа и метода главных факторов снизить размерность признакового пространства, обеспечив уровень информативности не менее 70%; При необходимости провести вращение пространства новых факторов; Дать экономическую интерпретацию факторам; Найти матрицу индивидуальных значений факторов. В отчет по работе добавить ответы на вопросы к защите (файл Пример Практика 1). Практическая часть В анализе данных зачастую стремятся к созданию упрощенной модели, которая максимально точно опишет реальное положение дел. Бывает, что признаки довольно сильно зависят друг от друга и их одновременное наличие избыточно, либо признаки зависят друг от друга не так строго и не так явно. Зная зависимости и их силу, мы можем выразить несколько признаков через один, слить воедино и работать уже с более простой моделью. Безусловно, избежать потерь информации, скорее всего не удастся, но минимизировать ее нам поможет метод PCA. Данный метод аппроксимирует n-размерное облако наблюдений до эллипсоида (тоже n-мерного), полуоси которого и будут являться будущими главными компонентами. И при проекции на такие оси (снижении размерности) сохраняется наибольшее количество информации. Зная, что и для чего мы делаем, можем приступить к решению задания с использованием метода главных компонент. Для начала нам необходимо наши данные внести в файл Exel, из которого JupyterNotebook (среда, в которой будем демонстрировать применение метода) будет их считывать. У нас есть выборка, что позднее будет преобразована в «датасет». Не забываем об импорте библиотек для работы с данными. Весь код для импорта библиотек и формирования «датасета» представлен на рисунке 1 и 2.  Рисунок 1 – Импорт библиотек  Рисунок 2 – Формирование «датасета» Масштабируем данные для того, чтобы некоторые параметры не были признаны «более важными» из-за различий в масштабе. Код представлен на рисунке 3, а результат – на рисунке 4.  Рисунок 3 – Код для масштабирования данных  Рисунок 4 – Масштабированные данные Построим ковариационную матрицу из масштабированных данных. Код для построения представлен на рисунке 5, а результат – на рисунке 6  Рисунок 5 – Код для построения ковариационной матрицы  Рисунок 6 – Ковариационная матрица Нашли собственные значения и векторы. Собственные векторы (главные компоненты) определяют направления нового пространства признаков, а собственные значения определяют их величину. Другими словами, собственные значения объясняют дисперсию данных вдоль новых осей признаков. Это означает, что соответствующее собственное значение говорит нам, сколько дисперсии включено в эту новую преобразованную функцию. Код для расчета и результат представлены на рисунке 7. 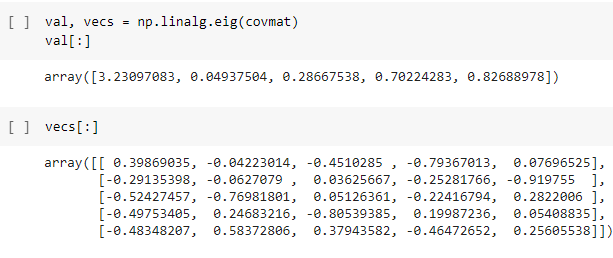 Рисунок 7 – Код для расчета собственных значений и векторов, результат выполнения Применим автоматизированный метод PCA для отбора 2 главных компонент.  Рисунок 8 – Код для отбора 2 главных компонент  Рисунок 9 - Рассчитанный процент «объясненной дисперсии» Визуализируем изображение двух главных компонент в двумерном пространстве. Код для визуализации представлен на рисунке 10, а результат – на рисунке 11.  Рисунок 10 – Код для визуализации главных компонент Рисунок 10 – Код для визуализации главных компонент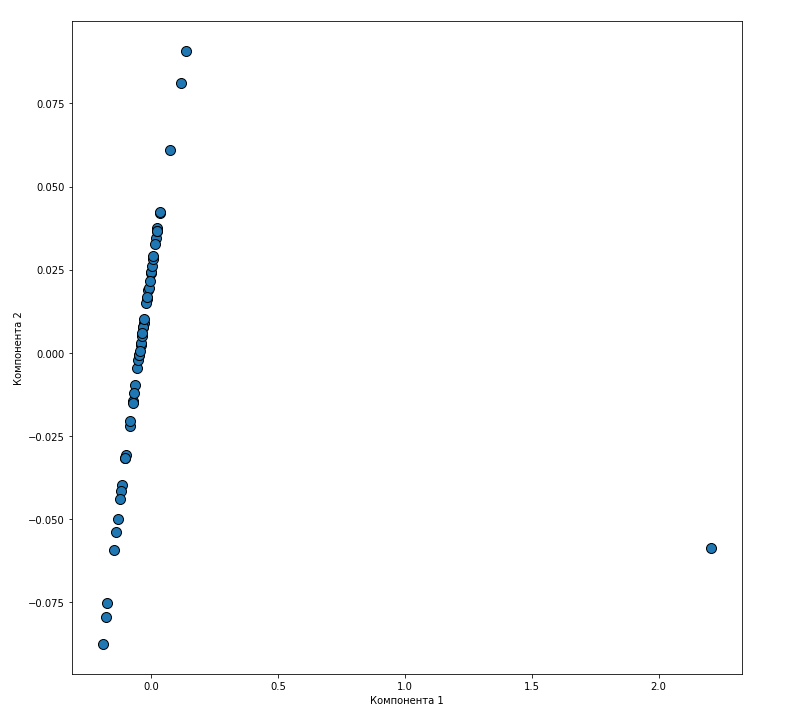 Рисунок 10 – Главные компоненты в двумерном пространстве  Рисунок 11 – Значения собственных векторов (вклад признаков) Исходя из значений собственных векторов, мы можем сделать вывод о значимости признаков в формировании главных компонент: на первую главную компоненту оказывает влияние Х1 (трудоемкость единицы продукции); на формирование второй главной компоненты оказывает влияние Х8 (среднегодовая численность ПП) и Х10 (среднегодовой фонд заработной платы ППП). Построив график расположения предприятий в пространстве двух компонент можно сделать вывод, что максимальная изменчивость достигается первой компонентой, а значит признаком Х1 (трудоемкость единицы продукции). Вывод: была снижена размерность признакового пространства с помощью метода главных компонент с минимальной потери информации. Вопросы 1. Какие параметры, аргументы и методы у класса PCA? Принципиальный компонентный анализ или PCA – это метод, используемый для уменьшения размерности большого набора данных. Сокращение количества компонентов или функций требует некоторой точности, а с другой стороны, делает большой набор данных более простым, легким для изучения и визуализации. Кроме того, это уменьшает вычислительную сложность модели, что ускоряет работу алгоритмов машинного обучения. Метод примечателен тем, что из исходного пространства данных мы формируем новое, но почти сохранившее свою информативность. Используем для этого стандартизацию данных (масштабирование), ковариационную матрицу, собственные векторы и собственные значения из ковариационной матрицы для вычислений, проецирование. 2. Как получить доступ к данным о векторах нагрузок главных компонент, а также к значениям главных компонент для наблюдений? Ответа нет. 3. Какие преобразования исходных данных выполнялись и почему? Выполнялась стандартизация (масштабирование), т.к. данные были в разных измерительных шкалах. 4. Какие функции можно использовать для визуализации полученных результатов? Использовались функции библиотеки seaborn (библиотека для создания статистических графиков на Python) как: – plt.figure () (создание области, в которой будет строиться график); – sns.scatterplot () (создание точек на графике). |
