Отчет по работе "Расчёт термодинамических функций по результатам измерений теплоёмкости методом адиабатической вакуумной калориметрии"
 Скачать 70.09 Kb. Скачать 70.09 Kb.
|
|
Отчет по работе “Расчёт термодинамических функций по результатам измерений теплоёмкости методом адиабатической вакуумной калориметрии” Цель работы – рассчитать стандартные термодинамические функции меди по результатам измерений теплоёмкости методом адиабатической калориметрии. Результаты расчетов Получение набора значений мольной теплоёмкости при различных температурах из первичных экспериментальных данных. В работе были использованы результаты измерения теплоёмкости селенида галлия в интервале температур от 14,51 до 308,26 К. Рассчитанные значения мольной теплоёмкости приведены в таблице 1. Таблица 1. Результаты расчёта мольной теплоёмкости для Ga2Se3
Экстраполяция к 0 К экспериментально измеренных значений теплоёмкости 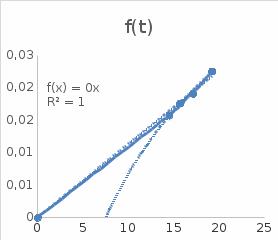 Зависимость Cp(T)/ T2 f(T) , тангенс угла наклона которой соответствует коэффициенту зависимости Cp T3, 9,73*104 Дж/(моль·К4). 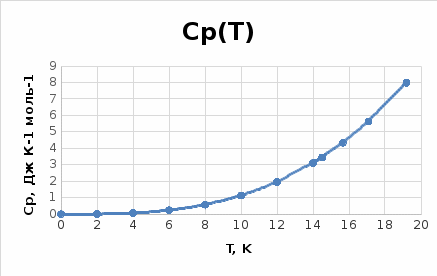 Зависимость теплоёмкости от температуры: точки – эксперимент, линия – расчёт по уравнению Cp T3. Аналитическое интегрирование теоретических зависимостей Cp(T) f(T) и Cp(T)/T f(T), полученных экстраполяцией к 0 К, в интервале от 0 К до Tn. Таблица 2. Рассчитанные значения Cp , STo и [HTo H0o] при низких температурах
Численное интегрирование первичных экспериментальных данных в координатах Cp(T) f(T) и Cp(T)/T f(T). Таблица 3. Стандартные термодинамические функции вещества (Ga2Se3), полученные с помощью численного интегрирования
Аппроксимация экспериментальных данных с помощью комбинации функций Планка−Эйнштейна. Таблица 4. Параметры функций Планка−Эйнштейна
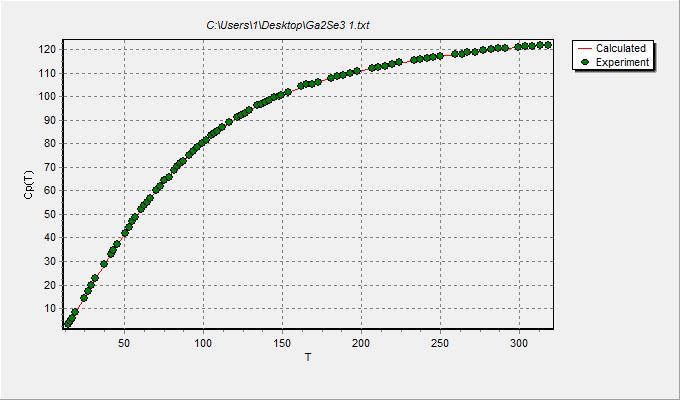 График зависимости Cp(T) (в Дж·К–1 ·моль–1) от температуры (в К) для селенида галлия: точки – экспериментальные значения, линия – расчёт с использованием функций Планка−Эйнштейна  График зависимости Cp(T)/T (в Дж·К–2 ·моль–1) от температуры (в К) для селенида галлия: точки – экспериментальные значения, линия – расчёт с использованием функций Планка−Эйнштейна Расчёт сглаженных значений термодинамических свойств изучаемого соединения Таблица 5. Стандартные термодинамические функции вещества (Ga2Se3), полученные при использовании функций Планка−Эйнштейна
Ответы на вопросы. 1. Приведите определение теплоёмкости. От каких факторов она зависит? Какова её размерность? Теплоемкость - коэффициент пропорциональности между количеством поглощённой теплоты Q и повышением температуры dT: Cx = (Q/ dT)x, где x обозначает конкретные условия, при которых проводится эксперимент (например, постоянство p, V и т.д.). Значение теплоемкости зависит от условий теплообмена. Теплоёмкость имеет размерность Дж·К−1 (или кал·К−1 ). Обычно величину теплоёмкости относят к определённой массе или количеству вещества: грамму или 4 молю. Поэтому удельная теплоёмкость имеет размерность Дж·К−1 ·г −1 , а мольная Дж·К−1 ·моль−1 . 2. Что такое теплоёмкости CV и Cp? Изохорную или изобарную теплоёмкость измеряют в ходе рассмотренного опыта? Как рассчитать разность CVCp? Приведите все известные Вам соотношения (в общем случае, для идеального газа, для твёрдых тел). Поскольку теплота не является свойством системы, а Q − полным дифференциалом, то теплоёмкость в общем случае в соответствии с её определением также не является свойством системы, а её значение зависит от условий теплообмена. Однако, в двух наиболее важных для практики процессах − при постоянном объёме и при постоянном давлении − теплоёмкость приобретает свойства функции состояния, и можно записать равенства: Cv=QV/dT=(U/T)v и Cp= Qp/dT (H/T)p, где CV и Cp − теплоёмкости соответственно при постоянном объёме и при постоянном давлении, U − внутренняя энергия, H − энтальпия системы. Величины QV/dT и Qp/dT могут быть определены экспериментально с помощью калориметра. Для решения практических задач в большинстве случаев достаточно знать порядок разности CVCp. Для идеального газа: CVCp=NR (уравнение Майера) Для твердого тела: CVCp=0,0214*Cp2*T/Tпл (эмпирическая формула Нернста) 3. За изменением какой величины ведут наблюдение в ходе калориметрического опыта? За разностью температур между калориметром и оболочкой железо родиевого термометра. Контролируется с помощью четырехспайной дифференциальной термопары (медь-железо)/хромель. 4. Какие способы аппроксимации экспериментальных данных по температурной зависимости теплоёмкости Вам известны? Опишите их. Результатом измерения теплоёмкости является набор значений Т и Cx (x = p, V). Аппроксимацию экспериментальных данных проводят разными способами: с использованием комбинаций функций Дебая и Эйнштейна, с помощью сплайн-функций, полиномиальных зависимостей и др. Наиболее распространённые полиномиальные зависимости с варьируемыми параметрами ai. С помощью программы «Cp_approx» можно выполнить аппроксимацию экспериментальных данных. Внеся экспериментальные данные Т и Ср, можно получить график Ср(Т). Расчеты покажут Ср (расчетную), Ср (экспериментальную) и разность между ними. Погрешность аппроксимации можно варьировать с помощью варьирования числа параметров функций Планка-Эйнштейна (коэффициентов аi и Thetta). 5. Сформулируйте правило Дюлонга и Пти. Для каких веществ оно выполняется? Правило Дюлонга-Пти: теплоёмкость многих одноатомных твёрдых кристаллических веществ Cp 26.4 24.9 Дж·К−1 ·моль−1. Для ряда веществ правило Дюлонга и Пти практически выполняется уже при 298 К. 6. Почему загрязнённость образца мешает точному определению теплоёмкости? Сформулируйте эмпирическое правило Неймана–Коппа для оценки теплоёмкости многоатомного кристалла. Правило Неймана−Коппа: теплоёмкость вещества в твёрдом состоянии приближённо равна сумме теплоёмкостей элементов, входящих в его состав. В частности, это правило означает, что Cp реакции с участием только твёрдых веществ приблизительно равна 0 и, следовательно, энтальпия такой реакции ( rH ) практически не зависит от температуры. Необходимую для подсчёта суммы вкладов информацию о теплоёмкостях простых веществ или составляющих можно взять из электронной базы данных NIST: http://webbook.nist.gov/chemistry/. 7. Каким образом можно экстраполировать к 0 К результаты измерений теплоёмкости в области гелиевых температур? В каком интервале температур и для каких типов структур выполняется закон кубов Дебая? Экстраполирование от 0К до первых экспериментальных значений производится по закону кубов Дебая. Линия тренда Сp = aT3, точка пересечения с осью ординат в (0,0). Значения а находятся как тангенс угла наклона линии Сp(T)/T2=f(T). Уравнение Эйнштейна для изохорной теплоемкости даёт хорошие результаты в области сравнительно высоких температур, объясняет стремление теплоёмкости к нулю при 0T , однако не описывает экспериментально наблюдаемую степенную зависимость Tn вблизи абсолютного нуля. Обычно 3n (закон кубов Дебая), но для веществ со слоистой (графит, чёрный фосфор, серый мышьяк, сурьма и др.) и цепочечной (серый селен, теллур и др.) структурой n может быть равно 2 или 1 соответственно. 8. Каковы, как правило, предельные значения теплоёмкости одноатомного кристалла при низких и высоких температурах? При высокой температуре (E/T 0) изохорная теплоёмкость одноатомного кристалла приближается к предельному значению 3R. 9. Для чего необходимы точные данные по температурной зависимости теплоёмкости? Какие термодинамические величины можно по ним рассчитать? С помощью температурной зависимости теплоемкости можно рассчитывать приращение энтальпии индивидуального вещества и его энтропию при заданной температуре. 10. Совпадают ли рассчитанные Вами разными способами термодинамические величины между собой, с литературными данными? Каковы возможные причины различия? Термодинамические величины, полученные расчетом, не совпадают с литературными данными. Несовпадение можно объяснить наличием примесей (правило Неймана-Коупа) и погрешностями, возникающими при использовании расчетных методов (варьирование числа параметров функций Планка-Эйнштейна). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
